In this section we describe an algorithm for sorting kN packets on
an N-node k-dimensional array with maximum side length M in
steps. The algorithm closely follows the algorithm of
Section 8 for sorting on the butterfly network.
For the sake of brevity, we omit many of the details.
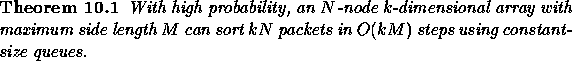
Sketch of proof:
The algorithm is essentially the same as the algorithm for sorting on
the butterfly. For simplicity, we assume that 
.
As before, there is a recursive subroutine for sorting
packets. We describe the action of the
subroutine on a 
-dimensional subcube. (A 
-dimensional
subcube of an array is a subgraph of the array consisting of
nodes whose labels 
share the same
value in some set of 
coordinates. For example, given a set
coordinates and a set 
of values, there is a subcube consisting of
those nodes 
such that 
for 
.) The array is lightly loaded by the factor of
to ensure that at each level of the recursion,
the number of packets entering any 
-dimensional subcube is at
most 
.
The first step is to choose a set of splitters. A set of
packets are randomly chosen to be splitter
candidates and then sorted by comparing every candidate with every
other candidate, which can be done in 
steps. Next,
every 
th candidate is selected to be a splitter.
The subcube routes packets on a leveled logical routing network as
described in Section 6. The splitters are placed
on the plateaus of the logical network, 
of them on plateau i. Since
there are only 
splitters, only the first 
plateaus get any, where 
is some fixed constant less than one.
On plateau 1, the jth splitter is assigned to all of the nodes
labeled 
, where 
for 
. A packet routes across dimension 1 edges on
plateau 1 until until it reaches a splitter that is larger than
itself. It then routes across dimension 2 edges to plateau 2.
Because dimension 1 edges do not appear in any later plateaus, each
of the M intervals is routed to a disjoint k-1 dimensional
subgraph of the logical network. On each of these subgraphs, M
splitters are positioned on plateau 2, and so on.
The subroutine calls itself recursively on subcubes with 
dimensions. The recursion terminates when the number of packets
entering a subcube is less than kM, in which case they are sorted
sequentially in 
time. There are 
levels to the
recursion. As before, we can estimate the time required by the algorithm by
assuming that the time spent on a 
-dimensional subcube is
equal to the expectation, 
. The time is given by the recurrence
which has solution 
. To rigorously bound the time
we would have to argue that delay does accumulate across the levels of the
recursion.
The algorithm for sorting kN packets calls the subroutine once.
First, 
packets are randomly chosen to be
candidates and sorted using the subroutine. Next, every 
th
candidate is selected to be a splitter. The splitters partition the
packets into intervals of size 
. Since 
, each interval has at most 
packets. Since
the 1-dimensional subcubes can each sort kM packets in 
steps using bubblesort, and 
, Columnsort can be applied to
sort all of the packets in 
steps.