This section offers a perspective on the DRAM model. We explore the analogy between PRAM's and universal networks on the one hand, and DRAM's and volume-universal networks on the other. We then discuss the issue of how data structures can be efficiently embedded in DRAM's--a problem not faced in the PRAM model. We also suggest how one might define the load factor for data structures other than graphs, such as matrices. Finally, we offer some comments on how some of our definitions and techniques might be extended or generalized.
The literature contains a large body of results concerning universal networks, such as the Boolean hypercube [29]. Universal networks are capable of simulating any PRAM program with at most polylogarithmic degradation in time (see, for example, the simulation [12] of an EREW-PRAM on a butterfly network). In light of this work, one might wonder why the DRAM model should be studied at all.
A potential problem with universal networks is that they may be difficult to physically construct on a large scale. The number of external connections (pins) on a packaging unit (chip, board, rack, cabinet) of an electronic system is typically much smaller than the number of components that the packaging unit contains, and can be made larger only with great cost. When a network is physically constructed, each packaging unit contains a subset of the processors of the network, and thus determines a cut of the network. For a universal network, the capacity of every cut must be nearly as large as the number of processors on the smaller side of the cut; otherwise, the load-factor lower bound would make it impossible to perform certain memory accesses in polylogarithmic time. Thus, when a universal network is physically constructed, the number of pins on a packaging unit must be nearly as large as the number of processors in the unit. Consequently, if all the pin constraints are met, a packaging unit cannot contain as many processors as might otherwise fit. Alternatively, if each packaging unit contains its full complement of processors, then pin limitations preclude the universal network from being assembled.
The impact of pin constraints can be modeled theoretically in the
three-dimensional VLSI model [16, 18]
where hardware cost is measured by volume and the pinboundedness of a
region is measured by its surface area. In this model, the largest
universal network that can fit in a given volume V has only about
nodes. In the two-dimensional VLSI model
[28], where pinboundedness is measured by perimeter, the
bound is even worse.
Since the density of processors in a physical implementation of a universal network is low, it is natural to wonder whether there are other networks that make more efficient use of hardware. Recently, it has been shown that fat-trees [10, 18] are such a class of ``volume-universal'' networks. A fat-tree of volume V can simulate any other network of comparable volume with only polylogarithmic degradation in time. (Figure 6 shows an area-universal fat-tree.) Thus, a fat-tree of volume V can efficiently simulate not only the universal networks with the same volume, but also some networks with almost V nodes. A key component in the proof that fat-trees are volume-universal is an algorithm for routing a set of messages on a fat-tree in time that is at most a polylogarithmic factor larger than the load factor.
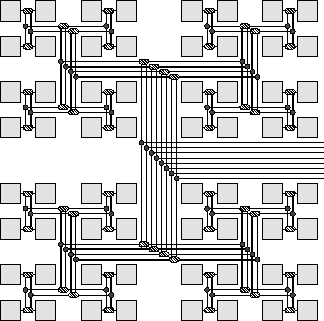
Figure 6: A fat-tree network. An area-universal fat-tree,
like the one shown, is capable of efficiently simulating any other
network of comparable area. Fat-trees are well modeled by distributed
random-access machines.
With a suitable assignment of capacities to cuts, the DRAM can abstract the essential communication characteristics of volume and area-universal networks without relying in detail on any particular network. Much as the PRAM can be viewed as an abstraction of a hypercube, in that algorithms for a PRAM can be implemented on a hypercube with only polylogarithmic performance degradation, the DRAM can be viewed as an abstraction of a volume or area-universal network. Fast, communication-efficient algorithms on a DRAM with the appropriate cut capacities translate directly to fast, communication-efficient algorithms on, for example, a fat-tree.
We now turn to the problem of embedding data structures in DRAM's, a problem that must be faced by users of conservative algorithms if the algorithms are to run quickly. In general, the problem of determining the best embedding for an arbitrary data structure is NP-complete, but for many common situations, good embeddings can be found. Moreover, there are many situations in which the input graph structure is simple and known a priori, and a good embedding may be easy to construct.
To illustrate how the embedding problem can be solved in certain practical situations, consider the class of DRAM's whose cut capacities correspond to area-universal fat-trees. For this class of DRAM's, the recursive structure of the underlying fat-tree network suggests that a divide-and-conquer approach be taken. For example, a subproblem in switch-level simulation of a VLSI circuit is the finding of electrically equivalent portions of the circuit. A naive divide-and-conquer embedding of the circuit on the fat-tree would yield small load factors for every cut. Thus, our conservative connected-components algorithm would never cause undue congestion in communicating messages in the underlying network, and the algorithm would run as fast as on an expensive, high-bandwidth network.
For some graphs, it can be proved that divide and conquer yields near-optimal embeddings on a fat-tree. Specifically, graphs for which a good separator theorem [20] exists can be embedded well. Examples include meshes, trees, planar graphs, and multigrids. Situations in which a mesh might be used include systolic array computation [15, 17] and image processing. Planar graphs and multigrids arise from the solution of sparse linear systems of equations based on the finite-element method. Consequently, conservative DRAM algorithms operating on good embeddings of these graphs would run fast on a fat-tree.
The algorithms presented in this paper operate primarily on graphs for which there is a natural definition of load factor. It is also possible to define the load factor of a data structure that contains no explicit pointers. For example, it is natural to superimpose a mesh on the matrix, as is suitable for systolic array computation [15, 17], and the load factor of the matrix can be defined as the load factor of the mesh.
For some algorithms, the running time may be better characterized as a function of the load factor of the output than the load factor of the input. As an example, consider the problem of sorting a linear list of elements. A natural question to ask is whether a list can be sorted in a polylogarithmic number of steps where at each step, the load factor is bounded by the load factor induced by the linear list together with the permutation determined by the sorted output. Such a sorting algorithm is known for fat-trees [13], but whether such an algorithm exists for general DRAM's is an open question.
Whereas the Shortcut Lemma presented in this paper holds for any network, for particular networks, other shortcut lemmas may hold. For example, another shortcut lemma for fat-trees is used in [21] to show that an optimal reordering of a linear list in a fat-tree can be determined efficiently by a conservative algorithm on the fat-tree.
As a final comment, we note that the notion of a conservative
algorithm may well be too conservative. As a practical matter, it is
probably not worth worrying whether every set of memory accesses is
conservative with respect to the input, as long as the load factor of
memory accesses is not much greater than the input load factor. For
example, a contraction tree is not conservative with respect to its
input tree (though the levels of the contraction tree are), but the
load factor of the contraction tree is at most 
times the
input load factor. Algorithms with this looser bound are somewhat
easier to code because of the relaxed constraint, and they should
perform comparably.