
Appears in Proceedings of "Supercomputing 98: High Performance
Networking and Computing", November 1998.
Girija J. Narlikar
narlikar@cs.cmu.edu
http://www.cs.cmu.edu/~girija
Guy E. Blelloch
blelloch@cs.cmu.edu
http://www.cs.cmu.edu/~guyb
In this paper, we study the performance of a native, lightweight POSIX threads (Pthreads) library on a shared memory machine running Solaris; to our knowledge, the Solaris library is one of the most efficient user-level implementations of the Pthreads standard available today. To evaluate this Pthreads implementation, we use a set of parallel programs that dynamically create a large number of threads. The programs include dense and sparse matrix multiplies, two N-body codes, a data classifier, a volume rendering benchmark, and a high performance FFT package. We find the existing threads scheduler to be unsuitable for executing such programs. We show how simple modifications to the Pthreads scheduler can result in significantly improved space and time performance for the programs; the modified scheduler results in as much as 44% less running time and 63% less memory requirement compared to the original Pthreads implementation. Our results indicate that, provided we use a good scheduler, the rich functionality and standard API of Pthreads can be combined with the advantages of dynamic, lightweight threads to result in high performance.
Recently, shared memory multiprocessors have been used to implement a wide range of high performance applications, such as [16, 20, 49, 54, 55]. The use of multithreading to program such applications is becoming popular, and POSIX threads or Pthreads [26] are now a standard supported on most platforms.
Pthreads may be implemented either at the kernel level, or as a user-level threads library. Kernel-level implementations require a system call to execute most thread operations, and the threads are scheduled by the kernel scheduler. This approach provides a single, uniform thread model with access to system-wide resources, at the cost of making thread operations fairly expensive. In contrast, most operations on user-level threads, including creation, synchronization and context switching, can be implemented in user space without kernel intervention, making them significantly cheaper than corresponding operations on kernel threads. Thus parallel programs can be written with a large number of lightweight, user-level Pthreads, leaving the scheduling and load balancing to the threads implementation, and resulting in simple, well structured, and architecture-independent code. A user-level implementation also provides the flexibility to choose a scheduler that best suits the application, independent of the kernel scheduler.
Lightweight and efficient user-level Pthreads packages are now available for shared memory programming [18, 31, 50]. However, most multithreaded parallel programs are still coded in a coarse-grained manner, with one thread per processor. Most programmers do not believe they will get high performance by simply expressing the parallelism as a large number of threads and leaving the scheduling and load balancing to the threads implementation. If threads accessing common data are scheduled on different processors, poor locality may limit the performance of the program. Further, the Pthreads scheduler may not be well suited to manage a large number of threads. Thus even multithreaded programs on shared memory machines are typically restricted to the SPMD programming style (e.g.,[53, 54]), and do not take advantage of lightweight threads implementations.
In this paper, we examine the applicability of lightweight, user-level Pthreads to express dynamic or irregular parallel programs, that is, programs that can be more simply expressed using a large number of lightweight threads. Since the Solaris Pthreads library is one of the most efficient user-level implementations of Pthreads available today, we decided to study the performance of seven multithreaded, parallel programs on a Sun Enterprise 5000 SMP running Solaris. The programs include dense and sparse matrix multiplies, two N-body codes, a data classifier, a volume rendering benchmark, and a high performance FFT package. We find that the only scheduler currently available in the library implementation, which uses a FIFO queue, creates a very large number of simultaneously active threads, resulting in high memory allocation, high resource contention, and poor speedup. We then describe simple modifications we made to the Solaris Pthreads implementation to improve space and time performance. The modified version of the Pthreads implementation uses a space-efficient scheduling mechanism [34] that results in a good speedup, while keeping memory allocation low. For example, for the dense matrix multiply program, the modified Pthreads scheduler reduces the running time on 8 processors compared to the original scheduler by 44%, and the memory requirement by 63%; this allows the program to run on 8 processors within 10% of the hand-optimized, platform-specific parallel BLAS3 library. Note that lowering memory requirement often improves the parallel running time due to fewer page and TLB misses, and less time spent waiting in the kernel for system calls related to memory allocation.
The parallel programs used in our experiments were written in a fine-grained style, and dynamically create a large number of Pthreads. We show that the programs, although simpler than their coarse grained versions, result in equivalent performance, provided the modified Pthreads scheduler is used. The threads in the parallel programs are expressed by the programmer with sufficient granularity to amortize thread costs and provide good locality within each thread. Our modified Pthreads implementation supports the full functionality of the original Pthreads library. Therefore, any existing Pthreads programs can be executed using our space-efficient scheduler, including programs with blocking locks and condition variables. Some previous implementations of space-efficient schedulers [11, 28, 34] do not support such blocking synchronizations. Our results indicate that, provided we use a good scheduler, the rich functionality and standard API of Pthreads can be combined with the advantages of dynamic, lightweight threads to result in high performance.
The remainder of this paper is organized as follows. Section 2 summarizes the advantages of using lightweight threads and gives an overview of related work on scheduling user-level threads. Section 3 describes the native Pthreads implementation on Solaris, and presents experimental results for one of the parallel benchmarks, namely, dense matrix multiply, using the existing Pthreads library. Section 4 briefly explains each modification we made to the Pthreads implementation, along with the resulting change in space and time performance for the benchmark. Section 5 describes the remaining parallel benchmarks and compares the performance of the original coarse-grained versions of the benchmarks with the versions rewritten to create a large number of threads, using both the original Pthreads implementation and the implementation with the modified scheduler. Section 6 summarizes our results and discusses some future work.
In this paper, we focus on the scheduling mechanisms used in lightweight threads packages written for shared memory machines. In particular, we are interested in implementing a scheduler for Pthreads that efficiently supports dynamic and irregular parallelism.
A variety of lightweight, user-level threads systems have been developed [6, 11, 14, 15, 25, 28, 32, 36, 39, 44, 52], including mechanisms to provide coordination between the kernel and the user-level threads library [2, 30, 48] Although the main goal of the threads schedulers in previous systems has been to achieve good load balancing and/or locality, a large body of work has also focused on developing scheduling techniques to conserve memory requirements. Since the programming model allows the expression of a large number of lightweight threads, the scheduler must take care not to create too many simultaneously active threads. This ensures that system resources like memory are not exhausted or do not become a bottleneck in the performance of the parallel program. For example, consider the serial execution of a simple computation, represented by the computation graph in Figure 1. Each node in the graph represents a computation within a thread, and each edge represents a dependency. The solid right-to-left edges represent the forking of child threads, while the dashed left-to-right edges represent joins between parent-child pairs. The vertical edges represent sequential dependencies within a single thread. Let us assume that a single global list of ready threads is maintained by the scheduler. If this list is implemented as a LIFO stack, the nodes are executed in a depth-first order. This results in as many d simultaneously active threads, where d is the maximum number of threads along any path in the graph1. In contrast, if the ready list were implemented as a FIFO queue, the system would execute the threads in a breadth-first order, creating a much larger number of threads. Thus a serial execution of the graph in Figure 1 using a FIFO queue would result in all 7 threads being simultaneously active, while a LIFO stack would result in at most 3 active threads.
The initial approaches to conserving memory were based on heuristics that work well for some applications, but do not provide guaranteed bounds on space [6, 19, 22, 28, 32, 38, 43, 45]. For example, Multilisp [43], a flavor of Lisp that supports parallelism through the future construct, uses per-processor LIFO stacks of ready threads to limit the parallelism. Lazy thread creation [22, 32] avoids allocating resources for a thread unless it is executed in parallel. Filaments [28], a package that supports fine-grained fork-join or loop parallelism using stateless threads, conserves memory and reduces overheads by coarsening and pruning excess parallelism.
Recent work has resulted in provably efficient scheduling techniques that provide upper bounds on the space required by the parallel computation [9, 11, 12, 13, 34]. Since there are several possible execution orders for lightweight threads in a computation with a high degree of parallelism, the provably space-efficient schedulers restrict the execution order for the threads to bound the space requirement. For example, the Cilk multithreaded system [11] guarantees a space bound of p x S1 on p processors for a program with a serial space requirement of S1, by maintaining per-processor stacks of ready threads. When a processor runs out of threads on its own stack, it picks another processor at random, and steals from the bottom of its stack. Various other systems use a similar work stealing strategy [25, 32, 36, 52] to control the parallelism. In [34], we present a provably space-efficient scheduling algorithm that uses a shared ``parallel'' stack and provides a space bound of S1 + O(pD) for a program with a critical path length of D. The algorithm prioritizes threads according to their serial execution order, and preempts threads when they run out of a preallocated memory quota. We showed that this algorithm results in lower space requirements for parallel benchmarks compared to Cilk, while maintaining good performance.

Figure 1:
An example computation graph with fork-join style of parallelism. A
right-to-left bold edge represents the fork of a child thread, while
a left-to-right dashed edge represents a join between a parent and child;
a sequential dependency within a thread is represented by a vertical edge.
For example, thread e is the child of thread b, which is the child of
thread a.
In this paper, we implement a variation of the scheduling algorithm from [34] in the context of Pthreads. While previous systems with space-efficient schedulers implement a restricted set of thread operations (such as fork and join), our work supports the standard and more general Pthreads API, which includes locks and condition variables. We modify an existing, native Pthreads library implementation by adding the space-efficient algorithm to its scheduler. Since the scheduling algorithm does not affect other important parts of the library, such as synchronization or signal handling, any existing Pthreads program can be run as is with our modified Pthreads scheduler. If the program is written to use a small number of threads, its performance using the new scheduler will be identical to the original scheduler. However, as we shall see later in the paper, a fine-grained program that dynamically creates and destroys a large number of Pthreads enjoys improved space and time performance with the modified Pthreads implementation.
The existing Pthreads interface allows the programmer to choose between a set of alternate scheduling policies for each thread. Two of these policies, SCHED_FIFO and SCHED_RR are well defined, and must respect the priorities assigned to each thread by the user. Our space-efficient scheduler could be provided as an implementation of the third policy, SCHED_OTHER, which is left unspecified by the POSIX standard. This paper focuses on a prioritized implementation of the space-efficient scheduler, that is, similar to the other two policies, runnable threads assigned higher priorities by the user will be scheduled before lower priority threads. However, threads within a single priority level are scheduled in a space-efficient manner. Thus, our policy can be used along with the other Pthread scheduling policies in a single program, as long as all threads within any priority level use the same scheduling policy.
The Solaris operating system contains kernel support for multiple threads within a single process address space [40]. One of the goals of the Solaris Pthreads implementation is to make the threads sufficiently lightweight so that thousands of them can be present within a process. The threads are therefore implemented by a user-level threads library so that common thread operations such as creation, destruction, synchronization and context switching can be performed efficiently without entering the kernel.
Lightweight, user-level Pthreads on Solaris are implemented by multiplexing them on top of kernel-supported threads called LWPs. The assignment of the lightweight threads to LWPs is controlled by the user-level Pthreads scheduler [50]. A thread may be either bound to an LWP (to schedule it on a system-wide basis) or may be multiplexed along with other unbound threads of the process on top of one or more LWPs. LWPs are scheduled by the kernel onto the available CPUs according to their scheduling class and priority, and may run in parallel on a multiprocessor. Figure 2 shows how threads and LWPs in a simple Solaris process may be scheduled. Process 1 has one thread bound to an LWP, and two other threads multiplexed on another LWP, while process 2 has three threads multiplexed on two LWPs. In this paper, we study and modify the policy used to schedule unbound Pthreads at a given priority level on top of LWPs.

Figure 2:
Scheduling of lightweight Pthreads and kernel-level LWPs in Solaris.
Threads are multiplexed on top of LWPs at the user level, while LWPs are
scheduled on processors by the kernel.
Since Solaris Pthreads are created, destroyed and synchronized by a user-level library without kernel intervention, these operations are significantly cheaper compared to the corresponding operations on kernel threads. Figure 3 shows the overheads for some Pthread operations on a 167 MHz UltraSPARC processor. Operations on bound threads involve operations on LWPs and require kernel intervention; they are hence more expensive than user-level operations on unbound threads. Note, however, that the user-level thread operations are still significantly more expensive than function calls; e.g., the thread creation time of 20.5 µsec. corresponds to over 3400 cycles on the 167 MHz UltraSPARC. The Pthreads implementation incurs this overhead for every thread expressed in the program, and does not attempt to automatically coarsen the parallelism by combining threads. Therefore, the overheads limit how fine-grained a task may be expressed using Pthreads without significantly affecting performance. It is left to the programmer to select the finest granularity for the threads such that the overheads remain insignificant, while maintaining portability, simplicity and load balance (see Section 5.3 for a discussion of thread granularity).
| Operation | Create | Context switch | Join | Semaphore sync. |
|---|---|---|---|---|
| Unbound thread | 20.5 | 9.0 | 6.0 | 19.0 | Bound thread | 170.0 | 11.0 | 8.5 | 55.0 |
Although more expensive than function calls, the thread overheads are low enough to allow the creation of many more threads than the number of processors during the execution of a parallel program, so that the job of scheduling these threads and balancing the load across processors may be left to the threads scheduler. Thus, this implementation of Pthreads is well-suited to express moderately fine-grained threads, resulting in simple and efficient code, particularly for programs with dynamic parallelism. For example, Figure 4 shows the pseudocode for a block-based, divide-and-conquer algorithm for matrix multiplication using dynamic parallelism: each parallel, recursive call is executed by forking a new thread. To ensure that the total overhead of thread operations is not significant, the parallel recursion on a 167 MHz UltraSPARC is terminated once the matrix size is reduced to 64 x 64 elements; beyond that point, an efficient serial algorithm is used to perform the multiplication2. The total time to multiply two 1024 x 1024 matrices with this algorithm on a single 167 MHz UltraSPARC processor, using our implementation of a LIFO scheduling queue and assuming a preallocated stack for every thread created, is 17.6 sec.; of this, the thread overheads are no more than 0.2 sec. The more complex but asymptotically faster Strassen's matrix multiply can also be implemented in a similar divide-and-conquer fashion with a few extra lines of code; coding it with static partitioning is significantly more difficult. Further, efficient, serial, machine-specific library routines can be easily plugged in to multiply the 64 x 64 submatrices at the base of the recursion tree. Note that the allocation of temporary space in the algorithm in Figure 4 can be avoided, but this would significantly add to the complexity of the code or reduce the parallelism.
Matrix_Mult(A, B, C, size) {
if (size <= K) serial_mult(A, B, C, size);
else
T = mem_alloc(size*size);
initialize smaller matrices as quadrants of A, B, C, and T;
hsize = size/2;
fork Matrix_Mult(A11, B11, C11, hsize);
fork Matrix_Mult(A11, B12, C12, hsize);
fork Matrix_Mult(A21, B12, C22, hsize);
fork Matrix_Mult(A21, B11, C21, hsize);
fork Matrix_Mult(A12, B21, T11, hsize);
fork Matrix_Mult(A12, B22, T12, hsize);
fork Matrix_Mult(A22, B22, T22, hsize);
fork Matrix_Mult(A22, B21, T21, hsize);
join with all forked child threads;
Matrix_Add(T, C);
mem_free(T);
}

Figure 4: Pseudocode for a divide-and-conquer parallel matrix multiply
(when the matrix size is a power of 2).
The Matrix_Add function is implemented similarly using
a parallel divide-and-conquer algorithm. The constant K to check for the
base condition of the recursion is set to 64 on a 167 MHz UltraSPARC.
We implemented the algorithm in Figure 4 on an 8-processor Sun Enterprise 5000 SMP with 2 GB of main memory. Each processor is a 167 MHz UltraSPARC with a 512 KB L2 cache. We selected the only scheduling mechanism available in the Solaris 2.5 Pthreads library, SCHED_OTHER, which uses a FIFO scheduling queue. Figure 5 (a) shows the speedup of the program with respect to the serial C version written with function calls instead of forks. The speedup was unexpectedly poor for a compute-intensive parallel program like matrix multiply. Further, as shown in Figure 5 (b), the maximum memory allocated by the program during its execution (e.g., 115 MB on 8 processors) significantly exceeded the memory allocated by the corresponding serial program (approx. 25 MB).

Figure 5: Performance of matrix multiply on an 8-processor Enterprise 5000
SMP using the native Solaris Pthreads implementation:
(a) speedup with respect to
a serial C version; (b) high water mark of total heap memory
allocation during the execution of the program.
``Serial'' is the space requirement of the serial program, and equals
the size of the 2 input matrices and 1 output matrix.
To detect the cause for the poor performance of the program, we used a profiling tool (Sun Workshop version 4.0) to obtain a breakdown of the execution time, as shown in Figure 6. The processors spend a significant portion of the time in the kernel making system calls. The most time-consuming system calls were those involved in memory allocation. We also measured the maximum number of threads active during the execution of the program: the Pthreads scheduler creates more than 4500 simultaneously active threads during execution on a single processor. In contrast, a simple, serial, depth-first execution of the program (in which a child preempts its parent as soon as it is forked) on a single processor should result in just 11 threads being simultaneously active. Both these measures indicate that the native Pthreads scheduler creates a large number of active threads, which all contend for allocation of stack and heap space, as well as for scheduler locks, resulting in poor speedup and high memory allocation. Note that even if a parallel program exhibits good speedups for a given problem size, it is important to minimize its memory requirement; otherwise, as the problem size increases, the performance may soon begin to suffer due to excessive TLB and page misses.

Figure 6:
A breakdown of execution times on up to 8 processors for matrix multiply.
``Compute'' is the percentage of time doing useful computation,
``system'' is the percentage of time spent in system calls, and
``sys-wait'' is the percentage of time spent waiting in the system.
``Other'' includes idle time, the time spent waiting on
user-level locks, and the time spent faulting in text and data pages.
The Solaris Pthreads implementation creates a very large number of active threads because it uses a FIFO scheduling queue. Further, when a parent thread forks a child thread, the child thread is added to the queue rather than being scheduled immediately. As a result, the computation graph is executed in a breadth-first manner. (This matrix multiply program has a computation graph similar to the one in Figure 1; at each stage 8 threads are forked instead of the 2 shown in the figure.)
To improve the time and space performance of such multithreaded applications a scheduling technique that creates fewer active threads, as well as limits their memory allocation, is necessary. We describe our experiments in using such a scheduling technique with the Solaris Pthreads library in the rest of the paper.
We modified the malloc and free library functions to keep track of a thread's memory quota, and fork dummy threads if necessary. The curve labelled ``New scheduler'' in Figure 7(a) shows that the speedup improves with this scheduler. Further, the memory requirement (see Figure 7(b)) is significantly lower, and no longer increases rapidly with the number of processors.
The improvements indicate that allowing the user to determine the default thread stack size may be useful. However, predicting the required stack size can be difficult for some applications. In such cases, instead of conservatively allocating an extremely large stack, a technique such as stacklets [22] or whole program optimization [24] could be used to dynamically and efficiently extend stacks.

| 
|
|---|
Figure 7: Performance of matrix multiply on an 8-processor Enterprise 5000
SMP using variations of the native Pthreads implementation:
(a) speedup with respect to a serial C version;
(b) high water mark of heap memory allocation during the execution of
the program.
The results were averaged over 3 consecutive runs of the program.
``Original'' is with the original scheduler,
``LIFO'' uses a LIFO scheduler, ``LIFO + small stk'' stands for
the LIFO scheduler with a reduced default stack size,
``New scheduler'' uses our new
space-efficient scheduler, and
``New + small stk'' uses the new scheduler with a reduced default stack
size.
We describe each benchmark with its experimental results; Figure 8 summarizes the results for all the benchmarks.
| Benchmark | Problem Size | Coarse gr. Speedup | Finer gr. + orig. sched. | Finer gr. + new sched. | ||
|---|---|---|---|---|---|---|
| Speedup | Threads | Speedup | Threads | |||
| Matrix Multiply | 1024 x 1024 matrix of doubles | --- | 3.65 | 1977 | 6.56 | 59 |
| Barnes Hut | N=100K, Plummer model | 7.53 | 5.76 | 860 | 7.80 | 34 |
| FMM | N=10K, 5 multipole terms | --- | 4.90 | 4348 | 7.45 | 24 |
| Decision Tree | 133,999 instances | --- | 5.23 | 94 | 5.25 | 70 |
| FFTW | N = 4096K | 6.27 | 5.84 | 224 | 5.94 | 14 |
| Sparse Matrix | 30K nodes, 151K edges | 6.14 | 4.41 | 55 | 5.96 | 32 |
| Vol. Render | 2563 volume, 3752 image | 6.79 | 5.73 | 131 | 6.72 | 25 |
This program simulates the interactions in a system of N bodies over several timesteps using the Barnes-Hut algorithm[5]. Each timestep has three phases: an octree is first built from the set of bodies, the force on each body is then calculated by traversing this octree, and finally, the position and velocity of each body is updated. We used the ``Barnes'' application code from the SPLASH-2 benchmark suite [53] in our experiments.
In the SPLASH-2 Barnes code, one Pthread is created for each processor at the beginning of the execution; the threads (processors) synchronize using a barrier after each phase within a timestep. Once the tree is constructed, the bodies are partitioned among the processors. Each processor traverses the octree to calculate the forces on the bodies in its partition, and then updates the positions and velocities of those bodies. It also uses its partition of bodies to construct the octree in the next timestep. Since the distribution of bodies in space may be highly non-uniform, the work involved for the bodies may vary to a large extent, and a uniform partition of bodies across processors leads to load imbalance. The Barnes code therefore uses a costzones partitioning scheme to partition the bodies among processors [47]. This scheme tries to assign to each processor a set of bodies that involve roughly the same amount of work, and are located close to each other in the tree to get better locality.
We modified the Barnes code so that, instead of partitioning the work across the processors, a new Pthread is created to execute each small, constant-sized unit of work. For example, in the force calculation phase, starting from the root of the octree, we recursively forked a new Pthread to compute forces on particles in each subtree. The recursion was terminated when the subtree had (on average) under 8 leaves. Since each leaf holds multiple bodies, this granularity is sufficient to amortize the cost of thread overheads and to provide good locality within a thread. Thus, we do not need any partitioning scheme in our code, since the large number of threads in each phase are automatically load balanced by the Pthreads scheduler. Further, no per-processor data structures were required in our code, and the final version was significantly simpler than the original code.
The simulation was run on a system of 100,000 bodies generated under the Plummer model [1] for four timesteps (as with the default Splash-2 settings, the first two timesteps were not timed). Figure 8 shows that our simpler approach achieves the same high performance as the original code, provided we use the space-efficient scheduler. Note that when the thread granularity is coarsened and therefore the number of threads is reduced, the performance of the original FIFO scheduler also improves significantly. However, as the problem size scales, unless the number of threads increases, the scheduler cannot balance the load effectively. In addition to forks and joins, this application uses Pthread mutexes in the tree building phase, to synchronize modifications to the partially built octree.
This application executes another N-Body algorithm called the Fast Multipole Method or FMM [23]. The FMM in three dimensions, although more complex, has been shown to perform fewer computations than the Barnes-Hut algorithm for simulations requiring high accuracy, such as electrostatic systems [8]. The main work in FMM involves the computation of local and multipole expansion series that describe the potential field within and outside a cell, respectively. We first wrote the serial C version for the uniform FMM algorithm, and then parallelized it using Pthreads. The parallel version is written to use a large number of threads, and we do not compare it here to any preexisting version written with one thread per processor. The program was executed on 10,000 uniformly distributed particles by constructing a tree with 4 levels and using 5 terms in the multipole and local expansions.
We describe each phase of the force calculation and how it is parallelized:
Since this algorithm involves dynamic memory allocation (in phase 3), we measured its space requirement with the original and new versions of the Pthreads implementation (see Figure 9(a)). As with matrix multiply, the new scheduling technique results in lower space requirement. The speedups with respect to the serial C version are included in Figure 8.

Figure 9:
Memory requirement for the FMM and Decision Tree benchmarks.
``Orig. sched.'' uses the Pthreads implementation with the original
FIFO scheduler, while ``New sched.'' uses the new space-efficient scheduler.
``Serial'' is the space requirement of the serial program.
Classification is an important data mining problem. We implemented a decision tree builder to classify instances with continuous attributes. The algorithm used is similar to ID3 [41], with C4.5-like additions to handle continuous attributes [42]. The algorithm builds the decision tree in a top-down, divide-and-conquer fashion, by choosing a split along the continuous-valued attributes based on the best gain ratio at each stage. The instances are sorted by each attribute to calculate the optimal split. The resulting divide-and-conquer computation graph is highly irregular and data dependent, where each stage of the recursion itself involves a parallel divide-and-conquer quicksort to split the instances. We used an input dataset from a speech recognition task [56]; it has 133,999 instances, each with 4 continuous attributes and a true/false classification. A thread is forked for each recursive call in the tree builder, as well as for each recursive call in quicksort. In both cases, we switch to serial recursion once the number of instances is reduced to 2000. Since a coarse-grained implementation of this algorithm would be highly complex, requiring explicit load balancing, we did not implement it. The 8-processor speedups obtained with the original and new schedulers are shown in Figure 8; both the schedulers provided good time performance; however, the new scheduler resulted in a lower space requirement (see Figure 9(b)).
The FFTW (``Fastest Fourier Transform in the West'') library [21] computes the one- and multidimensional complex discrete Fourier transform (DFT). The FFTW library is typically faster than all other publicly available DFT code, and is competitive or better than proprietary, highly optimized versions such as Sun's Performance Library code. FFTW implements the divide-and-conquer Cooley-Tukey algorithm [17]. The algorithm factors the size N of the transform into N = N1 x N2, and recursively computes N2 transforms of size N1, followed by N1 transforms of size N2. The package includes a version of the code written with Pthreads, which we used in our experiments. The FFTW interface allows the programmer to specify the number of threads to be used in the DFT. The code forks a Pthread for each recursive transform, until the specified number of threads are created; after that it executes the recursion serially. The authors of the library recommend using one Pthread per processor for optimal performance.

Figure 10:
Running times for three versions of the multithreaded, one-dimensional DFT
from the FFTW library on p processors: (1) using p threads, (2) using 256
threads with the original Pthreads scheduler, (3) using 256 threads with the
modified Pthreads scheduler.
We ran a one-dimensional DFT of size N = 225 in our experiments, using either p threads (where p = no. of processors), or 256 threads. Figure 10 shows the speedups over the serial version of the code for one to eight processors. Note that when p is a power of two, the problem size (which is also a power of two) can be uniformly partitioned among the processors using p threads, and being a regular computation, it does not suffer from load imbalance. Therefore, for p = 2, 4, 8, the version with p threads runs marginally faster. However, for all other p, the version with a larger number of threads can be better load balanced by the Pthreads implementation, and therefore performs better. This example shows that without any changes to the code, the performance becomes less sensitive to the number of processors when a large number of lightweight threads are used. The performance of this application was comparable with both the original and the new Pthreads schedulers (see Figure 8).
We timed 20 iterations of the product w = M x v , where M is a sparse, unsymmetric matrix and v and w are dense vectors. The code is a modified version of the Spark98 kernels [37] which are written for symmetric matrices. The sparse matrix in our experiments is generated from a finite element mesh used to simulate the motion of the ground after an earthquake in the San Fernando valley [3, 4]; it has 30,169 rows and 151,239 non-zeroes. In the coarse-grained version, one thread is created for each processor at the beginning of the simulation, and the threads execute a barrier at the end of each iteration. Each processor (thread) is assigned a disjoint and contiguous set of rows of M, such that each row has roughly equal number of nonzeroes. Keeping the sets of rows disjoint allows the results to be written to the w vector without locking.
In the fine-grained version, 128 threads are created and destroyed in each iteration. The rows are partitioned equally rather than by number of nonzeroes, and the load is automatically balanced by the threads scheduler (see Figure 8).
This application from the Splash-2 benchmark suite uses a ray casting algorithm to render a 3D volume [46, 53] . The volume is represented by a cube of volume elements, and an octree data structure is used to traverse the volume quickly. The program renders a sequence of frames from changing viewpoints. For each frame, a ray is cast from the viewing position through each pixel; rays are not reflected, but may be terminated early. Parallelism is exploited across these pixels in the image plane. Our experiments do not include times for the preprocessing stage which reads in the image data and builds the octree.
In the Splash-2 code, the image plane is partitioned into equal sized rectangular blocks, one for each processor. However, due to the nonuniformity of the volume data, an equal partitioning may not be load balanced. Therefore, every block is further split into tiles, which are 4 x 4 pixels in size. A task queue is explicitly maintained for each processor, and is initialized to contain all the tiles in the processor's block. When a processor runs out of work, it steals a tile from another processor's task queue. The program was run on a 2563 volume data set of a Computed Tomography head and the resulting image plane was 375 x 375 pixels.
In our fine-grained version, we created a separate Pthread to handle each set of 64 tiles (out of a total of 8836 tiles). Since rays cast through consecutive pixels are likely to access much of the same volume data, grouping a small set of tiles together is likely to provided better locality. However, since the number of threads created is much larger than the number of processors, the computation is load balanced across the processors by the Pthreads scheduler, and does not require the explicit task queues used in the original version. Figure 8 shows that the simpler, rewritten code runs as fast as the original code when the space-efficient scheduler is used.
To test the scalability of our scheduling approach, we ran our benchmarks on up to 16 processors of a Sun Enterprise 6000 server. The results are similar to those in Figure 8, and can be found in [35].
Lightweight threads allow for simple programming and good load balancing, but may incur high thread overheads and poor locality when the threads are too fine grained. Some systems support very fine-grained threads by automatically coarsening threads and executing them serially when there is sufficient parallelism [22, 28, 55]. In these systems, the thread overheads can be almost as low as a function call. However, the general Pthreads API makes implementing such optimizations difficult, and the cost of creation and destruction must be incurred for every Pthread expressed in the program. Therefore, in the experiments described so far, we adjusted the granularity of the Pthreads to amortize the cost of basic thread operations (such as creation, deletion, and synchronization). However, since our scheduler may schedule threads accessing common data on different processors, the granularity needed to be increased further for some applications to get good locality within each thread. For example, Figure 11 shows the variation of the speedup on 8 processors with thread granularity. Basic thread overheads at a finer granularity of 10 tiles per thread are at most 2.25% compared to the total execution time. Therefore, ideally, the execution on 8 processors at this granularity should be close to optimal. However, as shown in the figure, the granularity needs to be increased to around 60 tiles per thread to obtain optimal speedup. Since tiles close together in the image are likely to access common data, we expect that the slowdown at a finer granularity is mainly due to poor locality (and, to a smaller extent, due to contention on the scheduler lock). Note that, as expected, the original scheduler suffers from a bigger slowdown at the finer thread granularity, since it creates more simultaneously active threads. Further, both schedulers result in lower speedups due to load imbalance when the thread granularity is increased beyond approximately 130 tiles per thread.
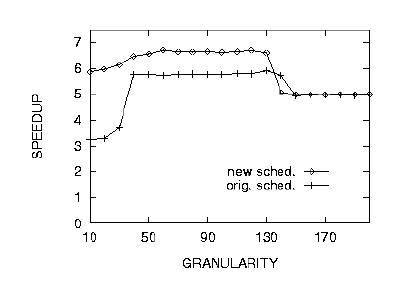
Figure 11:
Variation of speedup with thread granularity (defined as the maximum number of
4 x 4 pixel tiles processed by each thread) for the volume rendering
benchmark. ``Orig. sched.'' is the
speedup using the original FIFO scheduling queue, while ``New sched.''
is the speedup using our space-efficient scheduler.
Since basic Pthread operations cannot be avoided, the user must coarsen thread granularities to amortize their costs. However, ideally, we would not require the user to further coarsen threads for locality. Instead, the scheduling algorithm should schedule threads that are close in the computation graph on the same processor, so that good locality may be achieved. Then, for example, the curve in Figure 11 would not slope downwards as the granularity is reduced. We are currently working on such a space-efficient scheduling algorithm, and preliminary results indicate that good space and time performance can be obtained even at the finer granularity that simply amortizes thread operation costs.
Our space-efficient scheduler maintains a globally ordered list of threads; accesses to this list are serialized by a lock. Therefore, we do not expect such a serialized scheduler to scale well beyond 16 processors. A parallelized implementation of the scheduler, such as the one described in [33], would be required to ensure further scalability.
The effectiveness of our scheduler has been demonstrated on one SMP; future work involves studying its applicability to a scalable, NUMA multiprocessor by combining it with locality-based scheduling techniques such as [6, 29, 39]. For example, to schedule threads on a hardware-coherent cluster of SMPs, our scheduling algorithm could be used to maintain one shared queue on each SMP, and threads would be moved between SMPs only when required.
We have shown that our space-efficient scheduler is well suited for programs with irregular and dynamic parallelism. However, programs with other properties may require different schedulers for high performance. For example, we did not study the performance of our scheduler for benchmarks that make extensive use of locks or condition variables. A different scheduler may be required to efficiently execute such benchmarks. Further, an important advantage of user-level threads over kernel threads is their flexibility to support multiple schedulers. Therefore, it may be necessary to simplify the task of adding new schedulers to a threads implementation. A solution is to separate the scheduler from the rest of the threads implementation via a well-defined interface, similar to [7, 27].
We would like to thank the Berkeley NOW and Clumps projects for providing us access to their UltraSPARC-based workstations and Enterprise servers.