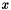 and
and 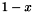 for a line, and so on).
for a line, and so on).

In the finite-element method, a PDE is written in weak form on an infinite-dimensional space and then discretized onto a finite-dimensional space as specified by the choice of Mesh and by the choice of basis function.
There are many possible weak formulations for any given PDE, for instance Galerkin or first-order least squares. Furthermore, there is then some freedom in choice of basis function (often constrained by stability considerations). Sundance is designed to allow great flexibility in choice of formulation and discretization method.
The unknown and variational (test) functions in a weak equation are represented by UnknownFunction and TestFunction objects, respectively. The first constructor argument to an UnknownFunction or TestFunction object is the BasisFamily with which it will be discretized. For example,
Expr T = new UnknownFunction(new Lagrange(1), "T");
A BasisFamily such as Lagrange is a geometry-independent specification of a basis function; the basis family object automatically hook to the low-level functions appropriate to the cell being integrated (e.g. 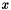 and
and 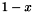 for a line, and so on).
for a line, and so on).
The continuous formulation of a finite-elements problem is as a weak equation, for example
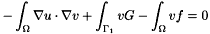
plus possible restrictions on the variations on specified boundary segments (see Boundary conditions below).
To represent a weak equation, use the Sundance Integral object. Assuming that the boundary segment 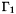 has been represented with a CellSet called gamma the equation above would be written
has been represented with a CellSet called gamma the equation above would be written
operator.
Since the integrals will be done with quadrature, you can give a specification of a quadrature family as an optional argument to Integral. For example,
Integral myEqn = Integral(someCellSet, v*sin(x), new GaussLegendre(8));
Integral myEqn = Integral(v*sin(4*x), new GaussLegendre(16)) + Integral(v*u, new GaussLegendre(2));
There are many ways to handle boundary conditions in finite-elements problems.
In Galerkin methods, Neumann BCs are easy: the BC 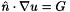 along a CellSet top is incorporated by adding
along a CellSet top is incorporated by adding
Integral(top, v*G)
Dirichlet BCs can done by replacing the weak equation on the boundary nodes with another weak equation representing the BCs. In Sundance, this is done with the EssentialBC object. To apply the weak condition 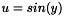 on the CellSet left, write
on the CellSet left, write
EssentialBC bc = EssentialBC(left, v*(u-sin(y)));
EssentialBC bc = EssentialBC(left, v*(u-sin(y)))
&& EssentialBC(right, v*(u-cos(y)));
In least-squares formulations, you can do dirichlet BCs in least-squares form (i.e., as just another Integral) or in essential form. Using the least-squares form has the advantage that your matrix remains SPD, but the BCs will not always be satisfied exactly.
You can also do Dirichlet BCs by introducing lagrange multipliers along the boundary. In this case, the BC becomes just another integral to be added to the weak equation. This method is sometimes useful, but produces indefinite matrices.

