Mimicking the case of upper bounds, we replace individual
conditional probabilities of the findings with lower-bounding
transformations, resulting in a lower-bounding expression
. Taking the product with P(d) and marginalizing
over d yields a lower bound on the likelihood:
We wish to maximize 
with respect to the variational
parameters q to obtain the tightest possible bound.
Our problem can be mapped onto a standard optimization problem
in statistics. In particular, treating d as a latent variable,
f as an observed variable, and q as a parameter vector, the
optimization of (or its logarithm) can be viewed as a
standard maximum likelihood estimation problem for a latent variable
model. It can be solved using the EM algorithm (Dempster, Laird, &
Rubin, 1977). The algorithm yields a sequence of variational parameters
that monotonically increase the objective function 
.
Within the EM framework, we obtain an update of the variational
parameters by maximizing the expected complete log-likelihood:
where 
denotes the vector of variational parameters
before the update, where the constant term is independent of the
variational parameters q and where the expectation is with respect
to the posterior distribution 
.
Since the variational parameters associated with the conditional
probabilities 
are independent of one another,
we can maximize each term in the above sum separately. Recalling the form
of the variational transformation (see Eq. (24)), we have:
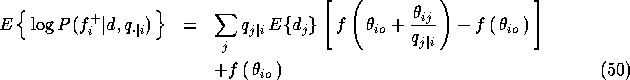
which we are to maximize with respect to 
while keeping the
expectations 
fixed. This optimization problem can be
solved iteratively and monotonically by performing the following
synchronous updates with normalization:
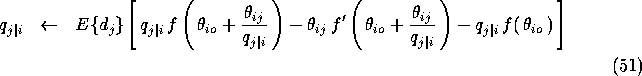
where f' denotes the derivative of f. (The update is guaranteed to be non-negative).
This algorithm can be easily extended to handle the case where not
all the positive findings have been transformed. The only new feature
is that some of the conditional probabilities in the products
and have been left intact,
i.e., not transformed; the optimization with respect to the variational
parameters corresponding to the transformed conditionals proceeds as
before.