


Next: Reducing Domino Problems to
Up: Consistency of - is
Previous: Domino Systems
Similar to proving undecidability by reduction of unbounded domino problems,
where defining infinite grids is the key problem, defining a torus of
exponential size is the key to obtaining a
 -completeness proof by
reduction of bounded domino problems.
-completeness proof by
reduction of bounded domino problems.
To be able to apply Corollary 3.3 to
 consistency for
consistency for
 ,
we must characterise the torus
,
we must characterise the torus
 with a
with a
 of polynomial size. To characterise
this torus, we use 2n concepts
of polynomial size. To characterise
this torus, we use 2n concepts
 and
and
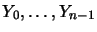 ,
where Xi (resp., Yi) codes the ith bit of the binary representation of
the X-coordinate (resp., Y-coordinate) of an element a.
,
where Xi (resp., Yi) codes the ith bit of the binary representation of
the X-coordinate (resp., Y-coordinate) of an element a.
For an interpretation
 and an element
and an element
 ,
we define
,
we define
 by
by
We use a well-known characterisation of binary addition
(e.g. [BGG97]) to relate the positions of the elements in the
torus:
Lemma 3.4
Let x,
x'
be natural numbers with binary representations
Then
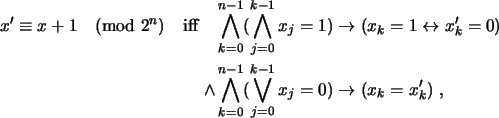
where the empty conjunction and disjunction are interpreted as true
and false, respectively.
Figure 3:
A TCBOX defining a torus of exponential size
![\begin{figure}\begin{center}
\framebox[\textwidth]{
$
\begin{array}{r@{\;}c@{...
... D_{\textit{north}}\xspace& = & \dots
\end{array} $ } \end{center} \end{figure}](img88.gif) |
The
 Tn is defined in Figure 3. The concept
C(0,0) is satisfied by all elements a of the domain for which
Tn is defined in Figure 3. The concept
C(0,0) is satisfied by all elements a of the domain for which
 holds.
C(2n-1,2n-1) is a similar concept, whose instances asatisfy
holds.
C(2n-1,2n-1) is a similar concept, whose instances asatisfy
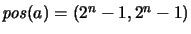 .
.
The concept
 is similar to
is similar to
 where the role
where the role
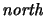 has
been substituted for
has
been substituted for
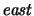 and variables Xi and Yi have been swapped.
The concept
and variables Xi and Yi have been swapped.
The concept
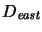 (resp.
(resp.
 )
enforces that, along the role
)
enforces that, along the role
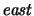 (resp.
(resp.
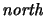 ), the value of
), the value of
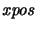 (resp.
(resp.
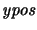 )
increases by one while
the value of
)
increases by one while
the value of
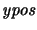 (resp.
(resp.
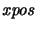 )
is unchanged. They are analogous to the
formula in Lemma 3.4.
)
is unchanged. They are analogous to the
formula in Lemma 3.4.
The following lemma is a consequence of the definition of
 and
Lemma 3.4.
and
Lemma 3.4.
Lemma 3.5
Let
 be an interpretation,
be an interpretation,
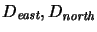 defined as in Figure 3, and
defined as in Figure 3, and
 .
.
The
 Tn defines a torus of exponential size in the following
sense:
Tn defines a torus of exponential size in the following
sense:
Lemma 3.6
Let Tn be the
 as defined in Figure 3. Let
as defined in Figure 3. Let
 be a model of Tn. Then
where
U
be a model of Tn. Then
where
U(2
n,2
n)
is the torus
 and S1
and S1,
S2 are
the horizontal and vertical successor relations on this torus.
Proof.
We show that the function pos is an isomorphism from
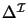 to
U(2n,2n). Injectivity of
to
U(2n,2n). Injectivity of
 is shown by induction on the
``Manhattan distance'' d(a) of the
is shown by induction on the
``Manhattan distance'' d(a) of the
 -value of an element a to the
-value of an element a to the
 -value of the upper right corner.
-value of the upper right corner.
For an element
 we define d(a) by
we define d(a) by
Note that
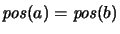 implies
d(a) = d(b). Since
implies
d(a) = d(b). Since
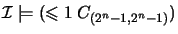 ,
there is at most one element
,
there is at most one element
 such that d(a)=0. Hence, there is exactly one element a such
that
such that d(a)=0. Hence, there is exactly one element a such
that
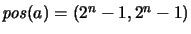 .
Now assume there are elements
.
Now assume there are elements
 such that
such that
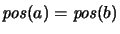 and
d(a) = d(b) > 0. Then either
and
d(a) = d(b) > 0. Then either
 or
or
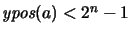 .
W.l.o.g., we assume
.
W.l.o.g., we assume
 .
From
.
From
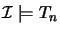 ,
it follows that
,
it follows that
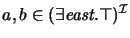 .
Let a1,b1 be elements such that
.
Let a1,b1 be elements such that
 and
and
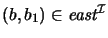 .
Since
d(a1) = d(b1) < d(a) and
.
Since
d(a1) = d(b1) < d(a) and
 ,
the induction
hypothesis yields a1 = b1. From
Lemma 3.5 it follows that
This also implies a=b because
,
the induction
hypothesis yields a1 = b1. From
Lemma 3.5 it follows that
This also implies a=b because
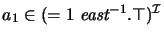 and
and
 .
Hence
.
Hence
 is injective.
To prove that
is injective.
To prove that
 is also surjective we use a similar technique.
This time, we use an induction on the distance from the lower left corner.
For each element
is also surjective we use a similar technique.
This time, we use an induction on the distance from the lower left corner.
For each element
 ,
we define:
,
we define:
d'(x,y) = x+y .
We show by induction that, for each
 ,
there is an
element
,
there is an
element
 such that
such that
 .
If
d'(x,y) = 0, then
x=y=0. Since
.
If
d'(x,y) = 0, then
x=y=0. Since
 ,
there is an element
,
there is an element
 such that
such that
 .
Now consider
.
Now consider
 with
d'(x,y) >0. Without loss of generality we assume x > 0 (if x = 0 then y > 0 must hold). Hence
with
d'(x,y) >0. Without loss of generality we assume x > 0 (if x = 0 then y > 0 must hold). Hence
 and
d'(x-1,y) <
d'(x,y). From the induction hypothesis, it follows that there is an element
and
d'(x-1,y) <
d'(x,y). From the induction hypothesis, it follows that there is an element
 such that
such that
 .
Then there must be an
element a1 such that
.
Then there must be an
element a1 such that
 and
Lemma 3.5 implies that
and
Lemma 3.5 implies that
 .
Hence
.
Hence
 is also surjective.
Finally,
is also surjective.
Finally,
 is indeed a homomorphism as an immediate consequence of
Lemma 3.5.
It is interesting to note that we need inverse roles only to guarantee that
pos is injective. The same can be achieved by adding the cardinality
restriction
is indeed a homomorphism as an immediate consequence of
Lemma 3.5.
It is interesting to note that we need inverse roles only to guarantee that
pos is injective. The same can be achieved by adding the cardinality
restriction
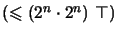 to Tn, from which the
injectivity of pos follows from its surjectivity and simple cardinality
considerations. Of course the size of this cardinality restriction would
only be polynomial in n if we assume binary coding of numbers. Also note
that we have made explicit use of the special expressive power of
cardinality restrictions by stating that, in any model of Tn, the
extension of
C(2n-1,2n-1) must have at most one element. This
cannot be expressed with a
to Tn, from which the
injectivity of pos follows from its surjectivity and simple cardinality
considerations. Of course the size of this cardinality restriction would
only be polynomial in n if we assume binary coding of numbers. Also note
that we have made explicit use of the special expressive power of
cardinality restrictions by stating that, in any model of Tn, the
extension of
C(2n-1,2n-1) must have at most one element. This
cannot be expressed with a
 -TBox consisting of terminological axioms.
-TBox consisting of terminological axioms.



Next: Reducing Domino Problems to
Up: Consistency of - is
Previous: Domino Systems
Stephan Tobies
May 02 2000
![]() -completeness proof by
reduction of bounded domino problems.
-completeness proof by
reduction of bounded domino problems.
![]() consistency for
consistency for
![]() ,
we must characterise the torus
,
we must characterise the torus
![]() with a
with a
![]() of polynomial size. To characterise
this torus, we use 2n concepts
of polynomial size. To characterise
this torus, we use 2n concepts
![]() and
and
![]() ,
where Xi (resp., Yi) codes the ith bit of the binary representation of
the X-coordinate (resp., Y-coordinate) of an element a.
,
where Xi (resp., Yi) codes the ith bit of the binary representation of
the X-coordinate (resp., Y-coordinate) of an element a.
![]() and an element
and an element
![]() ,
we define
,
we define
![]() by
by


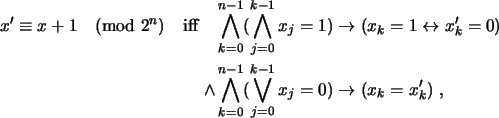
![]() Tn is defined in Figure 3. The concept
C(0,0) is satisfied by all elements a of the domain for which
Tn is defined in Figure 3. The concept
C(0,0) is satisfied by all elements a of the domain for which
![]() holds.
C(2n-1,2n-1) is a similar concept, whose instances asatisfy
holds.
C(2n-1,2n-1) is a similar concept, whose instances asatisfy
![]() .
.
![]() is similar to
is similar to
![]() where the role
where the role
![]() has
been substituted for
has
been substituted for
![]() and variables Xi and Yi have been swapped.
The concept
and variables Xi and Yi have been swapped.
The concept
![]() (resp.
(resp.
![]() )
enforces that, along the role
)
enforces that, along the role
![]() (resp.
(resp.
![]() ), the value of
), the value of
![]() (resp.
(resp.
![]() )
increases by one while
the value of
)
increases by one while
the value of
![]() (resp.
(resp.
![]() )
is unchanged. They are analogous to the
formula in Lemma 3.4.
)
is unchanged. They are analogous to the
formula in Lemma 3.4.
![]() and
Lemma 3.4.
and
Lemma 3.4.
![]() Tn defines a torus of exponential size in the following
sense:
Tn defines a torus of exponential size in the following
sense:
![]() to
U(2n,2n). Injectivity of
to
U(2n,2n). Injectivity of
![]() is shown by induction on the
``Manhattan distance'' d(a) of the
is shown by induction on the
``Manhattan distance'' d(a) of the
![]() -value of an element a to the
-value of an element a to the
![]() -value of the upper right corner.
-value of the upper right corner.
![]() we define d(a) by
we define d(a) by