We estimate the speedup factor that can be achieved using query pack execution in two steps: first we consider one-level packs, then we extend the results towards deeper packs.
Lower and upper bounds on the speedup factor that can be achieved by
executing a one-level pack instead of separate queries can be obtained as
follows. For a pack containing ![]() queries
queries
![]() , let
, let ![]() be the time needed to compute the first
answer substitution of
be the time needed to compute the first
answer substitution of ![]() if there are any, or to obtain failure
otherwise. Let
if there are any, or to obtain failure
otherwise. Let ![]() be the part of
be the part of ![]() spent within
spent within ![]() and
and ![]() the part of
the part of ![]() spent in
spent in ![]() . Then
. Then
![]() and
and
![]() with
with ![]() representing
the total time needed for executing all queries separately and
representing
the total time needed for executing all queries separately and ![]() the total time needed for executing the pack. Introducing
the total time needed for executing the pack. Introducing
![]() , which roughly represents the ratio of the computational
complexity in the shared part over that in the non-shared part, we have
, which roughly represents the ratio of the computational
complexity in the shared part over that in the non-shared part, we have
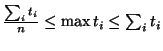 we know
we know
Thus the speedup factor is bounded from above by the branching factor
![]() and by the ratio
and by the ratio ![]() of computational complexity in the shared
part over the computational complexity of the non-shared part; and
a maximal speedup can be attained when
of computational complexity in the shared
part over the computational complexity of the non-shared part; and
a maximal speedup can be attained when
![]() (or,
(or, ![]() ), in other words when the
), in other words when the ![]() for all queries
are approximately equal.
for all queries
are approximately equal.
For multi-level packs, we can estimate the efficiency gain as follows.
Given a query ![]() , let
, let ![]() be defined as above (the total time for
finding 1 answer to
be defined as above (the total time for
finding 1 answer to ![]() or obtaining failure). Instead of
or obtaining failure). Instead of ![]() and
and
![]() , we now define
, we now define ![]() as the time spent on level
as the time spent on level ![]() of the
pack when solving
of the
pack when solving ![]() ; counting the root as level 0 and denoting the
depth of the pack with
; counting the root as level 0 and denoting the
depth of the pack with ![]() we have
we have
![]() .
Further define
.
Further define ![]() as the time spent on level
as the time spent on level ![]() or deeper:
or deeper:
![]() with
with ![]() the depth of the pack.
(Thus
the depth of the pack.
(Thus ![]() .). We will assume a constant branching factor
.). We will assume a constant branching factor ![]() in the pack. Finally, we define
in the pack. Finally, we define
![]() with
with ![]() . For simplicity, in the formulae we
implicitly assume that
. For simplicity, in the formulae we
implicitly assume that ![]() always ranges from 1 to
always ranges from 1 to ![]() with
with ![]() the
number of queries, unless explicitly specified otherwise. We then
have
the
number of queries, unless explicitly specified otherwise. We then
have
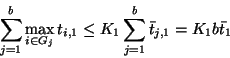 |
(5) |
| (6) |
| (7) |
| (8) |
| (9) |
Note that for ![]() we have
we have
| (10) |
| (11) |
Further, similar to ![]() in our previous analysis, define
in our previous analysis, define
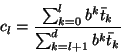 |
(12) |
Some algebra then gives
| (13) |
This inequality holds for all ![]() , hence we will find the best lower bound for
the speedup factor by maximizing the right hand side. Note that
, hence we will find the best lower bound for
the speedup factor by maximizing the right hand side. Note that ![]() increases and
increases and ![]() decreases monotonically with
decreases monotonically with ![]() .
It is clear that if at some point
.
It is clear that if at some point ![]() becomes much larger than 1, a
speedup factor of roughly
becomes much larger than 1, a
speedup factor of roughly ![]() is obtained. On the other hand,
if
is obtained. On the other hand,
if ![]() is smaller than 1, then the behaviour of
is smaller than 1, then the behaviour of ![]() is crucial.
Now,
is crucial.
Now,
Our conclusion is similar to that for the one-level pack. If for some
![]() ,
, ![]() , i.e., if in the upper part of the pack (up till level
, i.e., if in the upper part of the pack (up till level
![]() ) computations take place that are so expensive that they dominate
all computations below level
) computations take place that are so expensive that they dominate
all computations below level ![]() (even taking into account that the
latter are performed
(even taking into account that the
latter are performed ![]() times more often), then a speedup of
times more often), then a speedup of
![]() can be expected. If
can be expected. If ![]() , which will usually be the
case for all
, which will usually be the
case for all ![]() except those near
except those near ![]() , the speedup can roughly be
estimated as
, the speedup can roughly be
estimated as
![]() . The maximum of all these factors
will determine the actual speedup.
. The maximum of all these factors
will determine the actual speedup.