Minority over-sampling with replacement

Previous research [19,18] has discussed over-sampling with replacement and has noted that it doesn't significantly improve minority class recognition. We interpret the underlying effect in terms of decision regions in feature space. Essentially, as the minority class is over-sampled by increasing amounts, the effect is to identify similar but more specific regions in the feature space as the decision region for the minority class. This effect for decision trees can be understood from the plots in Figure 3.

**Figure 3:** a) Decision region in which the three minority class samples (shown by '+') reside after building a decision tree. This decision region is indicated by the solid-line rectangle. b) A zoomed-in view of the chosen minority class samples for the same dataset. Small solid-line rectangles show the decision regions as a result of over-sampling the minority class with replication. c) A zoomed-in view of the chosen minority class samples for the same dataset. Dashed lines show the decision region after over-sampling the minority class with synthetic generation.
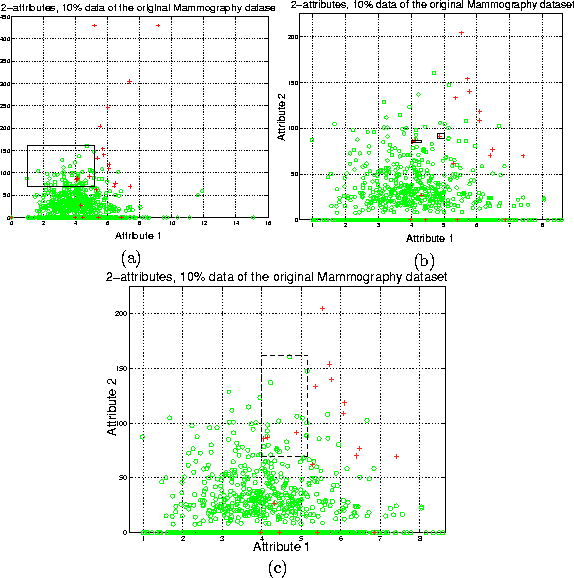
$\begin{figure} \centerline{ \parbox{2.5in}{ \centerline{\psfig{figure=10datac0.e... ...terline{\psfig{figure=10datac0s.eps,width=3in}} \centerline{(c)} } }\end{figure}$

The data for the plot in Figure 3 was extracted from a Mammography dataset [10]. The minority class samples are shown by + and the majority class samples are shown by o in the plot. In Figure 3(a), the region indicated by the solid-line rectangle is a majority class decision region. Nevertheless, it contains three minority class samples shown by '+' as false negatives. If we replicate the minority class, the decision region for the minority class becomes very specific and will cause new splits in the decision tree. This will lead to more terminal nodes (leaves) as the learning algorithm tries to learn more and more specific regions of the minority class; in essence, overfitting. Replication of the minority class does not cause its decision boundary to spread into the majority class region. Thus, in Figure 3(b), the three samples previously in the majority class decision region now have very specific decision regions.