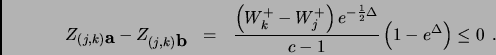Next: Proof of Theorem 6
Up: Appendix A
Previous: Proofsketch of Theorem 5
The proof of this lemma is quite straightforward, but we give it for completeness.  can be rewritten as
can be rewritten as
with
where
![$\Delta(j, k) = \vec{v}[j] - \vec{v}[k]$](img567.png) . Suppose for contradiction that for some
. Suppose for contradiction that for some 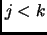 ,
,
 . We simply permute the two values
. We simply permute the two values ![$\vec{v}[j]$](img570.png) and
and ![$\vec{v}[k]$](img571.png) , and we show that the new value of
, and we show that the new value of  after,
after,
 , is not greater than
, is not greater than  before permuting,
before permuting,
 . The difference between
. The difference between
 and
and
 can be easily decomposed using the notation
can be easily decomposed using the notation
 (
(
 ) as the value of
) as the value of 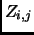 (eq. (27)) in
(eq. (27)) in
 , and
, and
 (
(
 ) as the value of
) as the value of 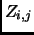 (eq. (27)) in
(eq. (27)) in
 . We also define:
. We also define:
 |
|
|
(28) |
We define in the same way
 . We obtain
. We obtain
Proving that
 can be obtained as follows. First,
can be obtained as follows. First,
We also have
 :
:
Here we have use the fact that
 . This shows that
. This shows that
 , and ends the proof of Lemma 1.
, and ends the proof of Lemma 1.



Next: Proof of Theorem 6
Up: Appendix A
Previous: Proofsketch of Theorem 5
©2002 AI Access Foundation and Morgan Kaufmann Publishers. All rights reserved.
![]() can be rewritten as
can be rewritten as