Model fragments

Model fragments are the building blocks with which scenario models are constructed. A model fragment $\mu$ is a tuple $\langle P^s,P^t,\Phi^s,\Phi^t,A,\Pi \rangle$ where $P^s=\{p_1^s,\ldots p_m^s\}$ is a set of variables called source-participants, $P^t=\{p_1^t,\ldots,p_n^t\}$ is a set of variables called target-participants, $\Phi^s=\{\phi_1^s,\ldots,\phi_v^s\}$ is a set of relations, called structural conditions, whose free variables are elements of $P^s$, $\Phi^t=\{\phi_1^t,\ldots,\phi_x^t\}$ is a set of relations, called postconditions, whose free variables are elements of $P^s\cup P^t$, $A=\{a_1,\ldots,a_y\}$ is a set of relations, called assumptions, and $\Pi=$ is a set of relations, called purpose-required properties, such that:

$$\forall \phi_i^t\in\Phi^t,\forall p_1^s,\ldots,\forall p_m^s,\exi... ...e\ldots\wedge\phi_v^s \rightarrow(a_1\wedge\ldots\wedge a_y\rightarrow\phi_i^t)$$ (12)

$$\forall \pi\in\Pi, \forall p_1^s,\ldots,\forall p_m^s,\forall p_1... ...ldots\wedge\phi_v^s\wedge a_1\wedge\ldots\wedge a_x\wedge\neg\pi\rightarrow\bot$$ (13)

Note that, in this work, each property definition $\langle P^s,\Phi,\pi\rangle$ is equivalent to a model fragment $\langle P^s,\{\},\Phi,\{\pi\},\{\},\{\} \rangle$.

For example, the model fragment below states that a population ?p can be described by two variables ?p-size (describing the size of ?p) and ?p-change (describing the rate of change in population size) and a differential equation

$$\frac{d}{dt}\texttt{?p-size}=\texttt{?p-change}$$

The usage of this partial scenario model is subject to two conditions: (1) the growth phenomenon is relevant with regard to ?p, and (2) the variable ?p-change is endogenous in the eventual scenario model. The former requirement is indicated by the relevance assumption and the latter by the purpose-required property:

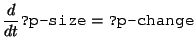(defModelFragment population-growth 
  :source-participants ((?p :type population)) 
  :assumptions ((relevant growth ?p)) 
  :target-participants ((?p-size :type variable) 
                        (?p-change :type variable)) 
  :postconditions ((size-of ?p-size ?p) 
                   (change-of ?p-change ?p) 
                   (d/dt ?p-size ?p-change))
  :purpose-required ((endogenous ?p-change)))

The purpose-required property is usually satisfied by additional model fragments, such as the one below:

(defModelFragment logistic-population-growth
  :source-participants ((?p :type population)
                        (?p-size :type variable)
                        (?p-change :type variable))
  :structural-conditions ((size-of ?p-size ?p)
                          (change-of ?p-births ?p))
  :assumptions ((model ?p-size logistic))
  :target-participants ((?r :type parameter)
                        (?k :type variable)
                        (?d :type variable))
  :postconditions ((capacity-of ?k ?p)
                   (density-of ?d ?p-size)
                   (== ?d (C-add (/ ?p-size ?k)))
    (== ?p-change (- (* ?r ?p-size (- 1 ?d))))))

Model fragments are rules of inference that describe how new knowledge can be derived from existing knowledge by committing the emerging model to certain assumptions. They are used to generate a space of possible models. Model fragments are instantiated by matching source-participants to existing participants in the scenario or an emerging model, and by matching the structural conditions to corresponding relations. For each possible instantiation, a new instance is generated for each of the target-participants, and where necessary, new instances are also created for the postconditions and assumptions. Such instances, as well as the inferential relationships between the instances of the source-participants, structural conditions and assumptions on the one hand, and those of the target-participants and postconditions on the other, are stored in an ATMS, forming the model space. This is to be further explained in section 3.3.1.

A model fragment is said to be applied if it is instantiated and the underlying assumptions hold. If a model fragment is applied, the instances of the target-participants and postconditions corresponding to the instantiation of that model fragment must be added to the resulting model. With respect to the above example, the model fragment that implements the logistic population growth model is instantiated whenever variables exist that describe the size and change in a population, and it is applied if the logistic model for population size has also been selected.

Note that in most compositional modellers, such as the ones devised by Heller and Struss [14,15]; Levy, Iwasaki and Fikes [24]; Nayak and Joskowicz [32]; and Rickel and Porter [35], model fragments represent direct translations of components of physical systems into influences between variables. Because the compositional modeller presented herein aims to serve as an ecological model repository, the contents of the model fragments employed differs from that of conventional compositional modellers in two important regards:

Firstly, model fragments contain partial models describing certain phenomena instead of influences. These partial models normally correspond to those developed in ecological modelling research. Typical examples include the logistic population growth model [43] and the Holling predation model [16] devised in the population dynamics literature.

Secondly, the partial models contained in the model fragments often need to be composed incrementally. For example, the aforementioned sample model fragment logistic-population-growth requires an emerging scenario model, which may be generated by the other sample model fragment population-growth. Thus, one model fragment, e.g. logistic-population-growth, can expand on the partial model contained in another, e.g. population-growth. Because of this feature, it is (correctly) presumed that no model fragment $\mu$ generates new relations that are preconditions of model fragments that $\mu$ expands on. Violating this presumption would make little sense in the context of the present application as it would imply a recursive extension of an emerging scenario model with the same set of variables and equations.