

Next: From model space to
Up: Inference
Previous: Inference
Scenario + Knowledge Base = Model Space
As previously stated, the aim of a compositional modeller is to
translate a scenario into a scenario model. Both are
representations of the system of interest though they model the system
at a different level of detail. The knowledge base provides the
foundation for translation. All the scenario models that can be
constructed from the given scenario, with regard to the knowledge
base, are stored in the model space.
A model space is an ATMS [7] containing all the
participants, relations and assumptions that can be instantiated from
a given scenario. In this work, the generalised version of the ATMS,
as introduced by de Kleer [8], is employed as it allows the use
of negations of nodes in the justifications. The algorithm
 describes how such a
model space can be created from a scenario
describes how such a
model space can be created from a scenario
 . It
first initialises the model space
. It
first initialises the model space 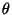 with the participant
instances (
with the participant
instances (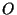 ) and the relation instances (
) and the relation instances (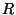 ) from the scenario.
Then, for each model fragment whose source-participants and structural
conditions match participants and relations already in
) from the scenario.
Then, for each model fragment whose source-participants and structural
conditions match participants and relations already in 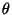 , new
instances of its target-participants, assumptions and postconditions
are added to
, new
instances of its target-participants, assumptions and postconditions
are added to 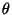 . Because each property definition
. Because each property definition
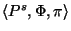 is equivalent to a model fragment
is equivalent to a model fragment
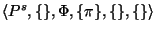 , this procedure applies to
property definitions as well as model fragments. Matching the
source-participants and structural conditions of a model fragment
, this procedure applies to
property definitions as well as model fragments. Matching the
source-participants and structural conditions of a model fragment
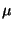 to the emerging model space is performed by the function
match
to the emerging model space is performed by the function
match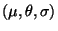 as specified below, where
as specified below, where 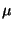 is
the model fragment being matched, and
is
the model fragment being matched, and 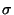 is a substitution from
the source-participants of
is a substitution from
the source-participants of 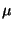 to participant instances.
to participant instances.
match |
|

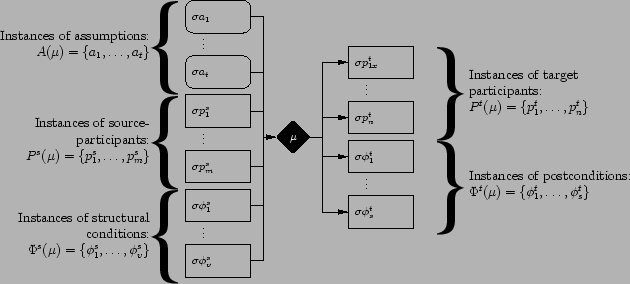
Figure 5:
Model fragment application
 |
Each match, specified by a model fragment  and a substitution
and a substitution
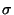 , is processed as follows:
, is processed as follows:
- For each assumption
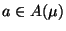 , a new node, denoting the
assumption instance
, a new node, denoting the
assumption instance 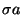 , is created and added to
, is created and added to 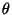 .
.
- Then, a new node
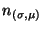 , denoting the instantiation of
, denoting the instantiation of
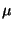 via substitution
via substitution 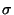 , is created, added to
, is created, added to 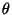 and
justified by the implication:
and
justified by the implication:
- Finally, a new instance for each target-participant
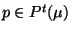 and for each postcondition
and for each postcondition
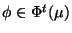 , provided
, provided
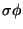 does not already exist in the model space
does not already exist in the model space 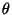 , is
created. For the target-participants, this involves creating a new
symbol for each new participant instance with the function
gensym
, is
created. For the target-participants, this involves creating a new
symbol for each new participant instance with the function
gensym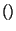 and extending
and extending 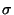 with the substitution
with the substitution
 gensym
gensym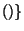 . A new node
. A new node 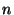 is created and added to
is created and added to
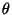 for each new participant instance
for each new participant instance  and for each
new instantiated relation
and for each
new instantiated relation
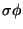 . Each of these nodes is
justified by the implication
. Each of these nodes is
justified by the implication
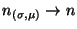 .
.
To illustrate this procedure, Figure 5
shows a graphical representation of the inferences that are
constructed by applying a model fragment
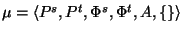 with respect to a substitution
with respect to a substitution
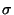 .
.
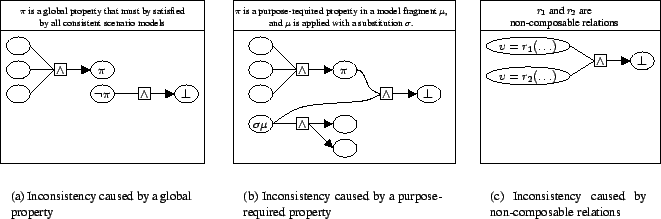
Figure 6:
Sources of inconsistency
 |
Once all possible applications of model fragments have been exhausted,
the inconsistencies in the model space are identified and recorded in
the ATMS. In the algorithm, nogoods are generated for each set
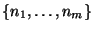 of inconsistent nodes, denoted
inconsistent
of inconsistent nodes, denoted
inconsistent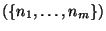 . There are three sources of
inconsistencies that are each reported to the ATMS in a different way:
. There are three sources of
inconsistencies that are each reported to the ATMS in a different way:
- Global properties: Let
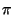 be an instance of a global
property that any scenario model must satisfy. Then, any
combination of assumptions and negations of assumptions that
prevents
be an instance of a global
property that any scenario model must satisfy. Then, any
combination of assumptions and negations of assumptions that
prevents 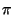 from being satisfied is inconsistent. Therefore,
inconsistent
from being satisfied is inconsistent. Therefore,
inconsistent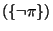 must be reported for any required
global property
must be reported for any required
global property 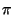 . This type of inconsistency is depicted
in Figure 6(a).
. This type of inconsistency is depicted
in Figure 6(a).
- Purpose-required properties: Any application of a model
fragment
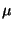 without satisfying its purpose-required properties
without satisfying its purpose-required properties
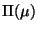 yields an inconsistency (see (13)).
Hence, for each node
yields an inconsistency (see (13)).
Hence, for each node
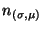 denoting the instantiation
of
denoting the instantiation
of 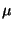 via substitution
via substitution 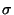 , and for each node
, and for each node
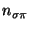 describing the appropriate instance of a
purpose-required property
describing the appropriate instance of a
purpose-required property
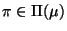 ,
inconsistent
,
inconsistent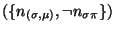 is
reported. This type of inconsistency is depicted in Figure
6(b).
is
reported. This type of inconsistency is depicted in Figure
6(b).
- Non-composable relations: In any mathematical formalism
designed to describe simulation models of dynamic systems, certain
combinations of relations may over-constrain the model, and hence,
be unsuitable for generating the behaviour of a system of interest.
Within the system dynamics and ODE formalisms used in this paper,
assignments of relations to the same variable are only composable if
those relations are explicitly deemed composable. In other words,
two relations
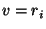 and
and 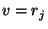 can only be combined with one
another if
can only be combined with one
another if  and
and 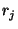 are composable. Examples of pairs of
non-composable relations include
are composable. Examples of pairs of
non-composable relations include
 |
and 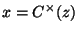 because because 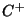 and and
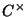 relations are not composable, and relations are not composable, and |
|
 |
and  because because  is not a composable relation. is not a composable relation. |
|
Combinations of such non-composable relations must be reported as an
inconsistency as well. This type of inconsistency is depicted in
Figure 6(c).
Figure 7:
Partial model space
 |
To illustrate the model space construction algorithm, Figure
7 presents a small sample model space.
It results from the application of the population-growth and
logistic-population-growth model fragments and the
endogenous property definition, which were described earlier,
for a single population ``frog''. If a larger scenario involving
multiple populations and relations between these populations were
specified, a similar partial model space would be generated for each
individual population.


Next: From model space to
Up: Inference
Previous: Inference
Jeroen Keppens
2004-03-01
![]() describes how such a
model space can be created from a scenario
describes how such a
model space can be created from a scenario
![]() . It
first initialises the model space
. It
first initialises the model space ![]() with the participant
instances (
with the participant
instances (![]() ) and the relation instances (
) and the relation instances (![]() ) from the scenario.
Then, for each model fragment whose source-participants and structural
conditions match participants and relations already in
) from the scenario.
Then, for each model fragment whose source-participants and structural
conditions match participants and relations already in ![]() , new
instances of its target-participants, assumptions and postconditions
are added to
, new
instances of its target-participants, assumptions and postconditions
are added to ![]() . Because each property definition
. Because each property definition
![]() is equivalent to a model fragment
is equivalent to a model fragment
![]() , this procedure applies to
property definitions as well as model fragments. Matching the
source-participants and structural conditions of a model fragment
, this procedure applies to
property definitions as well as model fragments. Matching the
source-participants and structural conditions of a model fragment
![]() to the emerging model space is performed by the function
match
to the emerging model space is performed by the function
match![]() as specified below, where
as specified below, where ![]() is
the model fragment being matched, and
is
the model fragment being matched, and ![]() is a substitution from
the source-participants of
is a substitution from
the source-participants of ![]() to participant instances.
to participant instances.
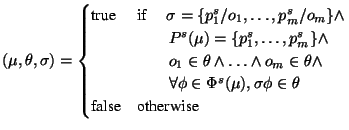

![]() and a substitution
and a substitution
![]() , is processed as follows:
, is processed as follows:
![]() of inconsistent nodes, denoted
inconsistent
of inconsistent nodes, denoted
inconsistent![]() . There are three sources of
inconsistencies that are each reported to the ATMS in a different way:
. There are three sources of
inconsistencies that are each reported to the ATMS in a different way: