| |
Effectiveness (F') |
Worst Case |
Traceability |
Size of |
| |
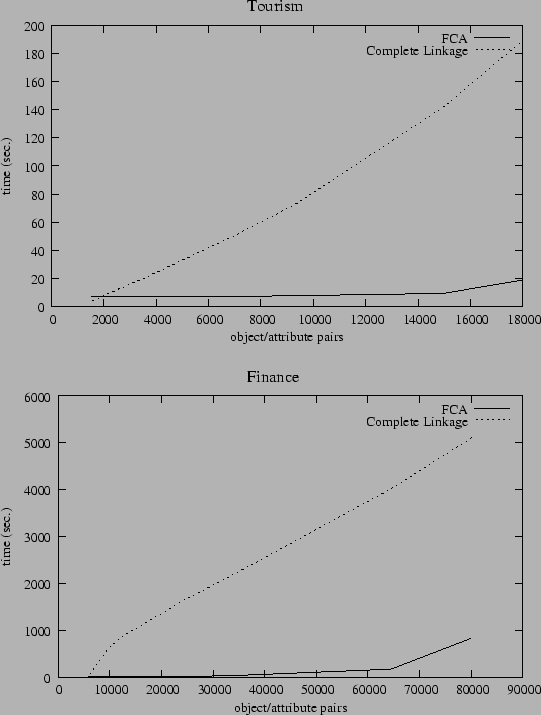
Tourism |
Finance |
Time Complexity |
|
Hierarchies |
| FCA |
44.69% |
38.85% |
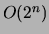 |
Good |
Large |
| Agglomerative Clustering: |
|
|
|
|
|
| Complete Linkage |
36.85% |
33.35% |
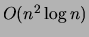 |
Fair |
Small |
| Average Linkage |
36.55% |
32.92% |
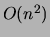 |
|
|
| Single Linkage |
38.57% |
32.15% |
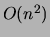 |
|
|
| Bi-Section-KMeans |
36.42% |
32.77% |
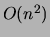 |
Weak |
Small |
|