


Next: Evaluation
Up: Learning Concept Hierarchies from
Previous: Formal Concept Analysis
Text Processing
As already mentioned in the introduction, in order to derive context attributes
describing the terms we are interested in, we make use of syntactic
dependencies between the verbs appearing in the text collection and the heads
of the subject, object and PP-complements they subcategorize. In fact, in
previous experiments [14]
we found that using all these dependencies in general leads to better
results than any subsets of them. In order to extract these
dependencies automatically, we parse the text with LoPar,
a trainable, statistical left-corner parser [54].
From the parse trees we then extract the syntactic dependencies between a
verb and its subject, object and PP-complement by using tgrep5.
Finally, we also lemmatize the verbs as well as the head of the
subject, object and PP-complement by looking up the lemma in the
lexicon provided with LoPar. Lemmatization maps a word to its
base form and is in this context used as a sort of normalization of the
text. Let's take for instance the following two sentences:
The museum houses an impressive collection of medieval and modern art.
The building combines geometric abstraction with classical references that allude to the Roman influence on the region.
After parsing these sentences, we would extract the following syntactic dependencies:
houses_subj(museum)
houses_obj(collection)
combines_subj(building)
combines_obj(abstraction)
combine_with(references)
allude_to(influence)
By the lemmatization step, references is mapped to its base form
reference and combines and houses to combine
and house, respectively, such that we yield as a result:
house_subj(museum)
house_obj(collection)
combine_subj(building)
combine_obj(abstraction)
combine_with(reference)
allude_to(influence)
In addition, there are three further important issues to consider:
- the output of the parser can be erroneous, i.e. not all derived
verb/argument dependencies are correct,
- not all the derived dependencies are 'interesting' in the
sense that they will help to discriminate between the different
objects,
- the assumption of completeness of information will never
be fulfilled, i.e. the text collection will never be big
enough to find all the possible occurrences (compare [65]).
To deal with the first two problems, we weight the object/attribute
pairs with regard to a certain information measure and
only process further those verb/argument relations for which this
measure is above some threshold  . In particular, we explore
the following three information measures (see [19,14]):
. In particular, we explore
the following three information measures (see [19,14]):
where
 .
.
Furthermore,  is the total number of occurrences of a term
is the total number of occurrences of a term
 as argument arg of a verb
as argument arg of a verb  ,
,  is
the number of occurrences of verb
is
the number of occurrences of verb  with such an argument and
with such an argument and
 is the relative frequency of a term
is the relative frequency of a term  compared to all
other terms. The first information measure is simply the
conditional probability of the term
compared to all
other terms. The first information measure is simply the
conditional probability of the term  given the argument
given the argument  of a verb
of a verb  . The second measure
. The second measure  is the so called
pointwise mutual information and was used by [34] for
discovering groups of similar terms. The third measure is inspired by the
work of [51] and introduces an additional factor
is the so called
pointwise mutual information and was used by [34] for
discovering groups of similar terms. The third measure is inspired by the
work of [51] and introduces an additional factor
 which takes into account all the terms appearing in the argument
position
which takes into account all the terms appearing in the argument
position  of the verb
of the verb  in question. In particular, the
factor measures the relative entropy of the prior and posterior (considering
the verb it appears with)
distributions of
in question. In particular, the
factor measures the relative entropy of the prior and posterior (considering
the verb it appears with)
distributions of  and thus the 'selectional strength' of the verb
at a given argument position. It is important
to mention that in our approach the values of all the above measures
are normalized into the interval [0,1].
The third problem requires smoothing of input data. In fact,
when working with text corpora, data sparseness is always an issue [65].
A typical method to overcome data sparseness is smoothing [43]
which in essence consists in assigning non-zero probabilities to unseen events.
For this purpose we apply the technique proposed by [21] in which mutually
similar terms are clustered with the result that an occurrence of an attribute
with the one term is also counted as an occurrence of that attribute with the
other term. As similarity measures we examine the Cosine, Jaccard, L1 norm, Jensen-Shannon divergence and Skew Divergence measures analyzed and described by [37]:
and thus the 'selectional strength' of the verb
at a given argument position. It is important
to mention that in our approach the values of all the above measures
are normalized into the interval [0,1].
The third problem requires smoothing of input data. In fact,
when working with text corpora, data sparseness is always an issue [65].
A typical method to overcome data sparseness is smoothing [43]
which in essence consists in assigning non-zero probabilities to unseen events.
For this purpose we apply the technique proposed by [21] in which mutually
similar terms are clustered with the result that an occurrence of an attribute
with the one term is also counted as an occurrence of that attribute with the
other term. As similarity measures we examine the Cosine, Jaccard, L1 norm, Jensen-Shannon divergence and Skew Divergence measures analyzed and described by [37]:
where
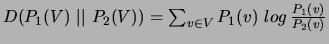 and
and

In particular, we implemented these measures using the variants relying
only on the elements  common to
common to  and
and  as described by [37]. Strictly speaking,
the Jensen-Shannon as well as the Skew divergences are dissimilarity functions
as they measure the average information loss when using one distribution
instead of the other. In fact we transform them into similarity measures
as
as described by [37]. Strictly speaking,
the Jensen-Shannon as well as the Skew divergences are dissimilarity functions
as they measure the average information loss when using one distribution
instead of the other. In fact we transform them into similarity measures
as  , where
, where  is a constant and
is a constant and  the dissimilarity function in question.
We cluster all the terms which are mutually similar with regard to the similarity measure in question, counting more attribute/object pairs than are actually found in the text and thus obtaining also non-zero frequencies for some
attribute/object pairs that do not appear literally in the corpus.
The overall result is thus a 'smoothing' of the relative frequency landscape by
assigning some non-zero relative frequencies to combinations of
verbs and objects which were actually not found in the corpus.
Here follows the formal definition of mutual similarity:
the dissimilarity function in question.
We cluster all the terms which are mutually similar with regard to the similarity measure in question, counting more attribute/object pairs than are actually found in the text and thus obtaining also non-zero frequencies for some
attribute/object pairs that do not appear literally in the corpus.
The overall result is thus a 'smoothing' of the relative frequency landscape by
assigning some non-zero relative frequencies to combinations of
verbs and objects which were actually not found in the corpus.
Here follows the formal definition of mutual similarity:
Definition 5 (Mutual Similarity)
Two terms

and
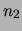
are mutually similar iff

and

.
According to this definition, two terms  and
and 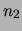 are mutually
similar if
are mutually
similar if  is the most similar term to
is the most similar term to 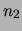 with regard to
the similarity measure in question and the other way round. Actually,
the definition is equivalent to the reciprocal similarity of
[34].
Figure 3 (left) shows an example of
a lattice which was automatically derived from a set of texts
acquired from http://www.lonelyplanet.com as well as
http://www.all-in-all.de, a web page containing information
about the history, accommodation facilities as well as activities
of Mecklenburg Vorpommern, a region in northeast Germany. We
only extracted verb/object pairs for the terms in Table
1 and used the conditional probability to weight
the significance of the pairs. For excursion, no dependencies
were extracted and therefore it was not considered when computing the lattice.
The corpus size was about a million words and the threshold used was
with regard to
the similarity measure in question and the other way round. Actually,
the definition is equivalent to the reciprocal similarity of
[34].
Figure 3 (left) shows an example of
a lattice which was automatically derived from a set of texts
acquired from http://www.lonelyplanet.com as well as
http://www.all-in-all.de, a web page containing information
about the history, accommodation facilities as well as activities
of Mecklenburg Vorpommern, a region in northeast Germany. We
only extracted verb/object pairs for the terms in Table
1 and used the conditional probability to weight
the significance of the pairs. For excursion, no dependencies
were extracted and therefore it was not considered when computing the lattice.
The corpus size was about a million words and the threshold used was  .
Assuming that car and bike are mutually similar, they would be clustered, i.e.
car would get the attribute startable and bike the attribute needable.
The result here is thus the lattice in Figure 3 (right), where
car and bike are in the extension of one and the same concept.
.
Assuming that car and bike are mutually similar, they would be clustered, i.e.
car would get the attribute startable and bike the attribute needable.
The result here is thus the lattice in Figure 3 (right), where
car and bike are in the extension of one and the same concept.
Figure 3:
Examples of lattices automatically derived from tourism-related texts without smoothing (left) and with smoothing (right)
 |



Next: Evaluation
Up: Learning Concept Hierarchies from
Previous: Formal Concept Analysis
Philipp Cimiano
2005-08-04



