Comparison

The best F-Measure for the tourism dataset is $F_{FCA,tourism}=40.52\%$ (at a threshold of $t=0.005$), corresponding to a precision of and a recall of $R_{FCA,tourism}=65.49\%$. For the finance dataset, the corresponding values are $F_{FCA,finance}=33.11\%$, $P_{FCA,finance}=29.93\%$ and $R_{FCA,finance}=37.05\%$. The Lexical Recall obviously also decreases with increasing threshold $t$ such that overall the F-Measure $F'$ also decreases inverse proportionally to $t$. Overall, the best results in terms of F' are $F'_{FCA,tourism}=44.69\%$ for the tourism dataset and $F'_{FCA,finance}=38.85\%$ for the finance dataset. The reason that the results on the finance dataset are slightly lower is probably due to the more technical nature of the domain (compared to the tourism domain) and also to the fact that the concept hierarchy to be learned is bigger.

Figure 9: Results for the FCA-based approach: F-Measure over Lexical Recall for the tourism and finance domains

In order to evaluate our FCA-based approach, we compare it with hierarchical agglomerative clustering and Bi-Section-KMeans. Hierarchical agglomerative clustering (compare [23]) is a similarity-based bottom-up clustering technique in which at the beginning every term forms a cluster of its own. Then the algorithm iterates over the step that merges the two most similar clusters still available, until one arrives at a universal cluster that contains all the terms. In our experiments, we use three different strategies to calculate the similarity between clusters: complete, average and single-linkage. The three strategies may be based on the same similarity measure between terms, i.e. the cosine measure in our experiments, but they measure the similarity between two non-trivial clusters in different ways. Single linkage defines the similarity between two clusters $P$ and $Q$ as $\max_{p\in P,q\in Q} sim(p,q)$, considering the closest pair between the two clusters. Complete linkage considers the two most dissimilar terms, i.e. $\min_{p\in P,q\in Q} sim(p,q)$. Finally, average-linkage computes the average similarity of the terms of the two clusters, i.e. $\frac{1}{\vert P\vert \vert Q\vert}\sum_{p\in P, q\in Q} sim(p,q)$. The reader should note that we prohibit the merging of clusters with similarity 0 and rather order them under a fictive universal cluster `root'. This corresponds exactly to the way FCA creates and orders objects with no attributes in common. The time complexity of a naive implementation of agglomerative clustering is $O(n^3)$, while efficient implementations have a worst-time complexity of $O(n^2 log n)$ for complete linkage as it requires sorting of the similarity matrix [22], $O(n^2)$ for average linkage if the vectors are length-normalized and the similarity measure is the cosine (see [43]) and O($n^2$) for single linkage (compare [55]).¹² Bi-Section-KMeans is defined as an outer loop around standard KMeans [58]. In order to generate $k$ clusters, Bi-Section-KMeans repeatedly applies KMeans. Bi-Section-KMeans is initiated with the universal cluster containing all terms. Then it loops: It selects the cluster with the largest variance¹³ and it calls KMeans in order to split this cluster into exactly two subclusters. The loop is repeated $k-1$ times such that $k$ non-overlapping subclusters are generated. As similarity measure we also use the cosine measure. The complexity of Bi-Section-KMeans is $O(k \cdot n)$. As we want to generate a complete cluster tree with $n$ clusters the complexity is thus O($n^2$). Furthermore, as Bi-Section-KMeans is a randomized algorithm, we produce ten runs and average the obtained results. We compare the different approaches along the lines of the measures described in Section 5. Figure 9 shows the results in terms of F-Measure $F$ over Lexical Recall for both domains and all the clustering approaches. In particular, it shows 8 data points corresponding to the thresholds 0.005, 0.01, 0.05, 0.1, 0.3, 0.5, 0.7 and 0.9. First of all it seems important to discuss the baselines for our approach. The baselines for our approach are the trivial concept hierarchies which are generated when no objects have attributes in common. Such trivial concept hierarchies are generated from threshold 0.7 on our datasets and by definition have a precision of 100% and a recall close to 0. While the baselines for FCA and the agglomerative clustering algorithm are the same, Bi-Section-KMeans is producing a hierarchy by random binary splits which results in higher F' values. These trivial hierarchies represent an absolute baseline in the sense that no algorithm could perform worse. It can also be seen in Figure 9 that our FCA-based approach performs better than the other approaches on both domains. As can be observed in Figure 10, showing recall over precision, the main reason for this is that the FCA-based approach yields a higher recall than the other a approaches, while maintaining the precision at reasonable levels.

Figure 10: Results for the FCA-based approach: Recall over precision for the tourism and finance domains

On the tourism domain, the second best result is achieved by the agglomerative algorithm with the single-linkage strategy, followed by the ones with average-linkage and complete-linkage (in this order), while the worst results are obtained when using Bi-Section-KMeans (compare Table 3). On the finance domain, the second best results are achieved by the agglomerative algorithm with the complete-linkage strategy followed by the one with the average-linkage strategy, Bi-Section-KMeans and the one with the single-linkage strategy (in this order). Overall, it is valid to claim that FCA outperforms the other clustering algorithms on both datasets. Having a closer look at Table 3, the reason becomes clear, i.e. FCA has a much higher recall than the other approaches, while the precision is more or less comparable. This is due to the fact that FCA generates a higher number of concepts than the other clustering algorithms thus increasing the recall. Interestingly, at the same time the precision of these concepts remains reasonably high thus also yielding higher F-Measures $F$ and $F'$.

Table 3: Results of the comparison of different clustering approaches

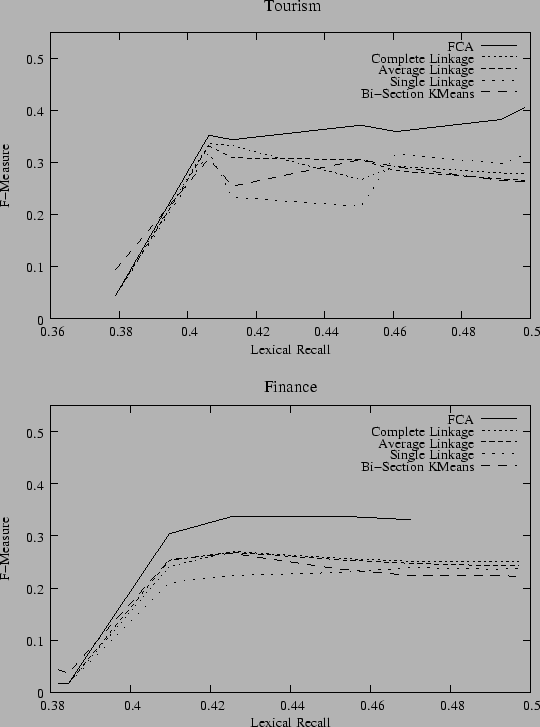
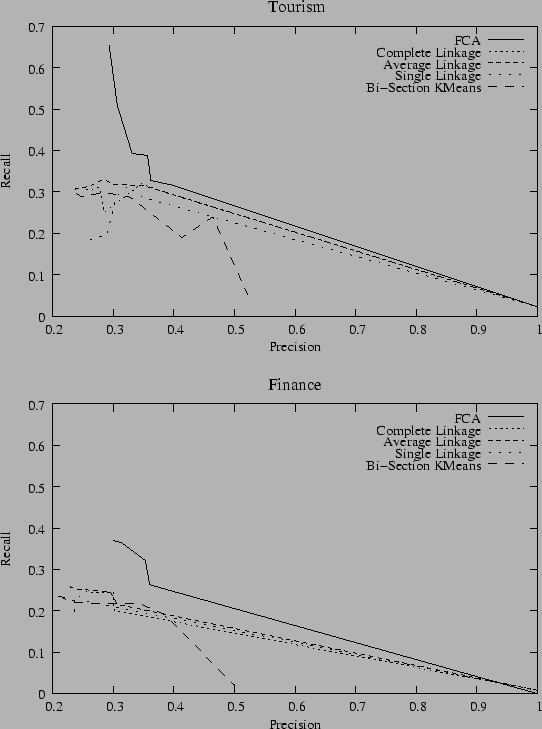
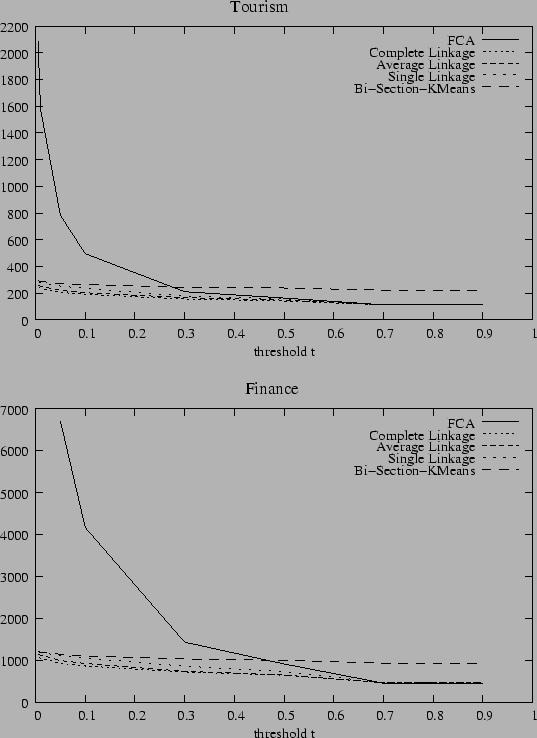
	Tourism				Finance
	P	R	F	F'	P	R	F	F'
FCA	29.33%	65.49%	40.52%	44.69%	29.93%	37.05%	33.11%	38.85%
Complete Link	34.67%	31.98%	33.27%	36.85%	24.56%	25.65%	25.09%	33.35%
Average Link	35.21%	31.45%	33.23%	36.55%	29.51%	24.65%	26.86%	32.92%
Single Link	34.78%	28.71%	31.46%	38.57%	25.23%	22.44%	23..75%	32.15%
Bi-Sec. KMeans	32.85%	28.71%	30.64%	36.42%	34.41%	21.77%	26.67%	32.77%

An interesting question is thus how big the produced concept hierarchies are. Figure 11 shows the size of the concept hierarchies in terms of number of concepts over the threshold parameter $t$ for the different approaches on both domains. It is important to explain why the number of concepts is different for the different agglomerative algorithms as well as Bi-Section-KMeans as in principle the size should always be $2 \cdot n$, where $n$ is the number of objects to be clustered. However, as objects with no similarity to other objects are added directly under the fictive root element, the size of the concept hierarchies varies depending on the way the similarities are calculated. In general, the sizes of the agglomerative and divisive approaches are similar, while at lower thresholds FCA yields concept hierarchies with much higher number of concepts. From threshold $0.3$ on, the sizes of the hierarchies produced by all the different approaches are quite similar. Table 4 shows the results for all approaches using the thresholds 0.3 and 0.5. In particular we can conclude that FCA also outperforms the other approaches on both domains when producing a similar number of concepts. In general, we have not determined the statistical significance of the results presented in this paper as FCA, in contrast to Bi-Section-K-Means, is a deterministic algorithm which does not depend on any random seeding. Our implementation of the agglomerative clustering algorithm is also deterministic given a certain order of the terms to be clustered. Thus, the only possibility to calculate the significance of our results would be to produce different runs by randomly leaving out parts of the corpus and calculating a statistical significance over the different runs. We have not pursued this direction further as the fact that FCA performs better in our setting is clear from the results in Table 3.

Table 4: Comparison of results at thresholds 0.3 and 0.5 in terms of F'

	Tourism		Finance
Threshold	0.3	0.5	0.3	0.5
FCA	37.53%	37.74%	37.59%	34.92%
Complete Link	36.85%	36.78%	33.05%	30.37%
Single Link	29.84%	35.79%	29.34%	27.79%
Average Link	35.36%	36.55%	32.92%	31.30%
Bi-Sec. KMeans	31.50%	35.02%	32.77%	31.38%

Figure 11: Sizes of concept hierarchies for the different approaches on the tourism and finance domains: number of concepts over threshold $t$