Blind minimality is essentially the best achievable with anytime
state-based solution methods which typically extend their envelope one
step forward without looking deeper into the future. Our translation
into a blind-minimal MDP can be trivially embedded in any of these
solution methods. This results in an `on-line construction' of the
MDP: the method entirely drives the construction of those parts of the
MDP which it feels the need to explore, and leave the others
implicit. If time is short, a suboptimal or even incomplete policy may
be returned, but only a fraction of the state and expanded state
spaces might be constructed. Note that the solution method should
raise an exception as soon as one of the reward formulae progresses to
 , i.e., as soon as an expanded state
, i.e., as soon as an expanded state
 is built such that
is built such that
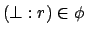 , since this acts as a
detector of unsuitable reward function specifications.
To the extent enabled by blind minimality, our approach allows for a
dynamic analysis of the reward formulae, much as in PLTLSTR [3]. Indeed, only the execution sequences feasible
under a particular policy actually explored by the solution method
contribute to the analysis of rewards for that policy. Specifically,
the reward formulae generated by progression for a given policy are
determined by the prefixes of the execution sequences feasible under
this policy. This dynamic analysis is particularly useful, since
relevance of reward formulae to particular policies (e.g. the optimal
policy) cannot be detected a priori.
The forward-chaining planner TLPlan [5] introduced the idea of using FLTL to specify domain-specific search control knowledge and formula progression to prune unpromising
sequential plans (plans violating this knowledge) from deterministic
search spaces. This has been shown to provide enormous time gains,
leading TLPlan to win the 2002 planning competition hand-tailored
track. Because our approach is based on progression, it provides an
elegant way to exploit search control knowledge, yet in the context of
decision-theoretic planning. Here this results in a dramatic reduction
of the fraction of the MDP to be constructed and explored, and
therefore in substantially better policies by the deadline.
We achieve this as follows. We specify, via a $-free formula
, since this acts as a
detector of unsuitable reward function specifications.
To the extent enabled by blind minimality, our approach allows for a
dynamic analysis of the reward formulae, much as in PLTLSTR [3]. Indeed, only the execution sequences feasible
under a particular policy actually explored by the solution method
contribute to the analysis of rewards for that policy. Specifically,
the reward formulae generated by progression for a given policy are
determined by the prefixes of the execution sequences feasible under
this policy. This dynamic analysis is particularly useful, since
relevance of reward formulae to particular policies (e.g. the optimal
policy) cannot be detected a priori.
The forward-chaining planner TLPlan [5] introduced the idea of using FLTL to specify domain-specific search control knowledge and formula progression to prune unpromising
sequential plans (plans violating this knowledge) from deterministic
search spaces. This has been shown to provide enormous time gains,
leading TLPlan to win the 2002 planning competition hand-tailored
track. Because our approach is based on progression, it provides an
elegant way to exploit search control knowledge, yet in the context of
decision-theoretic planning. Here this results in a dramatic reduction
of the fraction of the MDP to be constructed and explored, and
therefore in substantially better policies by the deadline.
We achieve this as follows. We specify, via a $-free formula
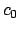 , properties which we know must be verified by paths feasible
under promising policies. Then we simply progress
, properties which we know must be verified by paths feasible
under promising policies. Then we simply progress 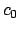 alongside the reward function specification, making e-states triples
alongside the reward function specification, making e-states triples
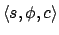 where
where  is a $-free formula
obtained by progression. To prevent the solution method from applying an
action that leads to the control knowledge being violated, the action
applicability condition (item 3 in Definition 5)
becomes:
is a $-free formula
obtained by progression. To prevent the solution method from applying an
action that leads to the control knowledge being violated, the action
applicability condition (item 3 in Definition 5)
becomes:
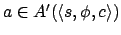 iff
iff 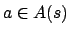 and
and
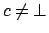 (the other changes are straightforward). For instance,
the effect of the control knowledge formula
(the other changes are straightforward). For instance,
the effect of the control knowledge formula
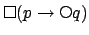 is to remove from consideration any feasible path in which
is to remove from consideration any feasible path in which  is
not followed by
is
not followed by  . This is detected as soon as violation occurs,
when the formula progresses to
. This is detected as soon as violation occurs,
when the formula progresses to  . Although this paper focuses
on non-Markovian rewards rather than dynamics, it should be noted that
$-free formulae can also be used to express non-Markovian
constraints on the system's dynamics, which can be incorporated in our
approach exactly as we do for the control knowledge.
Sylvie Thiebaux
2006-01-20
. Although this paper focuses
on non-Markovian rewards rather than dynamics, it should be noted that
$-free formulae can also be used to express non-Markovian
constraints on the system's dynamics, which can be incorporated in our
approach exactly as we do for the control knowledge.
Sylvie Thiebaux
2006-01-20