A Class of Reward-Normal Formulae
The existing decision procedure [41] for determining
whether a formula is reward-normal is guaranteed to terminate
finitely, but involves the construction and comparison of automata and
is rather intricate in practice. It is therefore useful to give a
simple syntactic characterisation of a set of constructors for
obtaining reward-normal formulae even though not all such formulae are
so constructible.
We say that a formula is material iff it contains no  and no temporal operators - that is, the material formulae are the
boolean combinations of atoms.
We consider four operations on behaviours representable by formulae of
$FLTL. Firstly, a behaviour may be delayed for a specified number of
timesteps. Secondly, it may be made conditional on a material trigger.
Thirdly, it may be started repeatedly until a material termination
condition is met. Fourthly, two behaviours may be combined to form
their union. These operations are easily realised syntactically by
corresponding operations on formulae. Where
and no temporal operators - that is, the material formulae are the
boolean combinations of atoms.
We consider four operations on behaviours representable by formulae of
$FLTL. Firstly, a behaviour may be delayed for a specified number of
timesteps. Secondly, it may be made conditional on a material trigger.
Thirdly, it may be started repeatedly until a material termination
condition is met. Fourthly, two behaviours may be combined to form
their union. These operations are easily realised syntactically by
corresponding operations on formulae. Where 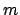 is any material
formula:
is any material
formula:
We have shown [41] that the set of reward-normal formulae
is closed under delay, cond (for any material 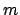 ), loop (for any material
), loop (for any material 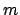 ) and union, and also that the
closure of
) and union, and also that the
closure of 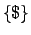 under these operations represents a class of
behaviours closed under intersection and concatenation as well as
union.
Many familiar reward-normal formulae are obtainable from
under these operations represents a class of
behaviours closed under intersection and concatenation as well as
union.
Many familiar reward-normal formulae are obtainable from  by
applying the four operations. For example,
by
applying the four operations. For example,
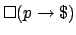 is
is
![$\mbox{{\sf loop}}[\mbox{$\bot$},\mbox{{\sf cond}}[p,\mbox{\$}]]$](img460.png) .
Sometimes a paraphrase is necessary. For example,
.
Sometimes a paraphrase is necessary. For example,
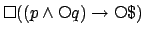 is not of the required form
because of the
is not of the required form
because of the
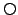 in the antecedent of the conditional, but the
equivalent
in the antecedent of the conditional, but the
equivalent
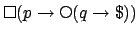 is
is
![$\mbox{{\sf loop}}[\mbox{$\bot$},\mbox{{\sf cond}}[p,\mbox{{\sf
delay}}[\mbox{{\sf cond}}[q,\mbox{\$}]]]]$](img463.png) . Other cases are not so
easy. An example is the formula
. Other cases are not so
easy. An example is the formula
![$\neg p \makebox[1em]{$\mathbin{\mbox{\sf U}}$}(p
\wedge \mbox{\$})$](img239.png) which stipulates a reward the first time
which stipulates a reward the first time  happens and which is not
at all of the form suggested. To capture the same behaviour using the
above operations requires a formula like
happens and which is not
at all of the form suggested. To capture the same behaviour using the
above operations requires a formula like
![$(p \rightarrow \mbox{\$})
\wedge (\raisebox{0.6mm}{$\scriptstyle \bigcirc$}(p \rightarrow \mbox{\$}) \makebox[1em]{$\mathbin{\mbox{\sf U}}$}p)$](img464.png) .
Sylvie Thiebaux
2006-01-20
.
Sylvie Thiebaux
2006-01-20
![\begin{eqnarray*}
\mbox{{\sf delay}}[f] & = & \raisebox{0.6mm}{$\scriptstyle \b...
...\sf U}}$}m \\
\mbox{{\sf union}}[f_1,f_2] & = & f_1 \wedge f_2
\end{eqnarray*}](img458.png)