We start with some notation and definitions. Given a finite set  of
states, we write
of
states, we write  for the set of finite sequences of states over
for the set of finite sequences of states over
 , and
, and 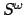 for the set of possibly infinite state sequences.
Where `
for the set of possibly infinite state sequences.
Where ` ' stands for a possibly infinite state sequence in
' stands for a possibly infinite state sequence in
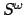 and
and  is a natural number, by `
is a natural number, by ` ' we mean the
state of index
' we mean the
state of index  in
in  , by `
, by ` ' we mean the prefix
' we mean the prefix
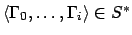 of
of  .
.
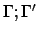 denotes the concatenation of
denotes the concatenation of 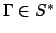 and
and
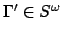 .
.
Subsections
Sylvie Thiebaux
2006-01-20