A Markov decision process of the type we consider is a 5-tuple
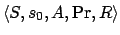 , where
, where  is a finite set of fully
observable states,
is a finite set of fully
observable states, 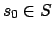 is the initial state,
is the initial state,  is a finite
set of actions (
is a finite
set of actions (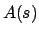 denotes the subset of actions applicable in
denotes the subset of actions applicable in
 ),
),
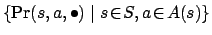 is a family of
probability distributions over
is a family of
probability distributions over  , such that
, such that  is the
probability of being in state
is the
probability of being in state  after performing action
after performing action  in
state
in
state  , and
, and
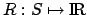 is a reward function such that
is a reward function such that
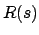 is the immediate reward for being in state
is the immediate reward for being in state  . It is well
known that such an MDP can be compactly represented using dynamic
Bayesian networks [18,11] or
probabilistic extensions of traditional planning languages,
see e.g., [37,45,50].
A stationary policy for an MDP is a function
. It is well
known that such an MDP can be compactly represented using dynamic
Bayesian networks [18,11] or
probabilistic extensions of traditional planning languages,
see e.g., [37,45,50].
A stationary policy for an MDP is a function
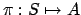 , such
that
, such
that
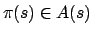 is the action to be executed in state
is the action to be executed in state  . The
value
. The
value 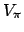 of the policy at
of the policy at 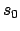 , which we seek to maximise, is
the sum of the expected future rewards over an infinite horizon,
discounted by how far into the future they occur:
, which we seek to maximise, is
the sum of the expected future rewards over an infinite horizon,
discounted by how far into the future they occur:
where
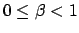 is the discount factor controlling the
contribution of distant rewards.
Sylvie Thiebaux
2006-01-20
is the discount factor controlling the
contribution of distant rewards.
Sylvie Thiebaux
2006-01-20
![\begin{displaymath}
V_\pi(s_0) = \lim_{n\rightarrow\infty} \makebox[1em]{$\mathb...
...n} \beta^{i} R(\Gamma_i) \mid \pi, \Gamma_{0} = s_{0} \bigg{]}
\end{displaymath}](img33.png)