Robotics and Control

In recent years there have been many robotics and control applications that have used reinforcement learning. Here we will concentrate on the following four examples, although many other interesting ongoing robotics investigations are underway.

1. Schaal and Atkeson [100] constructed a two-armed robot, shown in Figure 11, that learns to juggle a device known as a devil-stick. This is a complex non-linear control task involving a six-dimensional state space and less than 200 msecs per control decision. After about 40 initial attempts the robot learns to keep juggling for hundreds of hits. A typical human learning the task requires an order of magnitude more practice to achieve proficiency at mere tens of hits.

   The juggling robot learned a world model from experience, which was generalized to unvisited states by a function approximation scheme known as locally weighted regression [25, 82]. Between each trial, a form of dynamic programming specific to linear control policies and locally linear transitions was used to improve the policy. The form of dynamic programming is known as linear-quadratic-regulator design [97].

     
   Figure 11: Schaal and Atkeson's devil-sticking robot. The tapered stick is hit alternately by each of the two hand sticks. The task is to keep the devil stick from falling for as many hits as possible. The robot has three motors indicated by torque vectors .
   

2. Mahadevan and Connell [71] discuss a task in which a mobile robot pushes large boxes for extended periods of time. Box-pushing is a well-known difficult robotics problem, characterized by immense uncertainty in the results of actions. Q-learning was used in conjunction with some novel clustering techniques designed to enable a higher-dimensional input than a tabular approach would have permitted. The robot learned to perform competitively with the performance of a human-programmed solution. Another aspect of this work, mentioned in Section 6.3, was a pre-programmed breakdown of the monolithic task description into a set of lower level tasks to be learned.
3. Mataric [73] describes a robotics experiment with, from the viewpoint of theoretical reinforcement learning, an unthinkably high dimensional state space, containing many dozens of degrees of freedom. Four mobile robots traveled within an enclosure collecting small disks and transporting them to a destination region. There were three enhancements to the basic Q-learning algorithm. Firstly, pre-programmed signals called progress estimators were used to break the monolithic task into subtasks. This was achieved in a robust manner in which the robots were not forced to use the estimators, but had the freedom to profit from the inductive bias they provided. Secondly, control was decentralized. Each robot learned its own policy independently without explicit communication with the others. Thirdly, state space was brutally quantized into a small number of discrete states according to values of a small number of pre-programmed boolean features of the underlying sensors. The performance of the Q-learned policies were almost as good as a simple hand-crafted controller for the job.
4. Q-learning has been used in an elevator dispatching task [29]. The problem, which has been implemented in simulation only at this stage, involved four elevators servicing ten floors. The objective was to minimize the average squared wait time for passengers, discounted into future time. The problem can be posed as a discrete Markov system, but there are states even in the most simplified version of the problem. Crites and Barto used neural networks for function approximation and provided an excellent comparison study of their Q-learning approach against the most popular and the most sophisticated elevator dispatching algorithms. The squared wait time of their controller was approximately 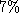less than the best alternative algorithm (``Empty the System'' heuristic with a receding horizon controller) and less than half the squared wait time of the controller most frequently used in real elevator systems.
5. The final example concerns an application of reinforcement learning by one of the authors of this survey to a packaging task from a food processing industry. The problem involves filling containers with variable numbers of non-identical products. The product characteristics also vary with time, but can be sensed. Depending on the task, various constraints are placed on the container-filling procedure. Here are three examples:
   • The mean weight of all containers produced by a shift must not be below the manufacturer's declared weight W.
   • The number of containers below the declared weight must be less than .
   • No containers may be produced below weight W'.

   Such tasks are controlled by machinery which operates according to various setpoints. Conventional practice is that setpoints are chosen by human operators, but this choice is not easy as it is dependent on the current product characteristics and the current task constraints. The dependency is often difficult to model and highly non-linear. The task was posed as a finite-horizon Markov decision task in which the state of the system is a function of the product characteristics, the amount of time remaining in the production shift and the mean wastage and percent below declared in the shift so far. The system was discretized into 200,000 discrete states and local weighted regression was used to learn and generalize a transition model. Prioritized sweeping was used to maintain an optimal value function as each new piece of transition information was obtained. In simulated experiments the savings were considerable, typically with wastage reduced by a factor of ten. Since then the system has been deployed successfully in several factories within the United States.

Some interesting aspects of practical reinforcement learning come to light from these examples. The most striking is that in all cases, to make a real system work it proved necessary to supplement the fundamental algorithm with extra pre-programmed knowledge. Supplying extra knowledge comes at a price: more human effort and insight is required and the system is subsequently less autonomous. But it is also clear that for tasks such as these, a knowledge-free approach would not have achieved worthwhile performance within the finite lifetime of the robots.

What forms did this pre-programmed knowledge take? It included an assumption of linearity for the juggling robot's policy, a manual breaking up of the task into subtasks for the two mobile-robot examples, while the box-pusher also used a clustering technique for the Q values which assumed locally consistent Q values. The four disk-collecting robots additionally used a manually discretized state space. The packaging example had far fewer dimensions and so required correspondingly weaker assumptions, but there, too, the assumption of local piecewise continuity in the transition model enabled massive reductions in the amount of learning data required.

The exploration strategies are interesting too. The juggler used careful statistical analysis to judge where to profitably experiment. However, both mobile robot applications were able to learn well with greedy exploration--always exploiting without deliberate exploration. The packaging task used optimism in the face of uncertainty. None of these strategies mirrors theoretically optimal (but computationally intractable) exploration, and yet all proved adequate.

Finally, it is also worth considering the computational regimes of these experiments. They were all very different, which indicates that the differing computational demands of various reinforcement learning algorithms do indeed have an array of differing applications. The juggler needed to make very fast decisions with low latency between each hit, but had long periods (30 seconds and more) between each trial to consolidate the experiences collected on the previous trial and to perform the more aggressive computation necessary to produce a new reactive controller on the next trial. The box-pushing robot was meant to operate autonomously for hours and so had to make decisions with a uniform length control cycle. The cycle was sufficiently long for quite substantial computations beyond simple Q-learning backups. The four disk-collecting robots were particularly interesting. Each robot had a short life of less than 20 minutes (due to battery constraints) meaning that substantial number crunching was impractical, and any significant combinatorial search would have used a significant fraction of the robot's learning lifetime. The packaging task had easy constraints. One decision was needed every few minutes. This provided opportunities for fully computing the optimal value function for the 200,000-state system between every control cycle, in addition to performing massive cross-validation-based optimization of the transition model being learned.

A great deal of further work is currently in progress on practical implementations of reinforcement learning. The insights and task constraints that they produce will have an important effect on shaping the kind of algorithms that are developed in future.