[Next] [Up] [Previous]

[*]

Proof of Theorem 

 

Without loss of generality, we assume in this proof that all variables are declared as evidence variables. To prove this soundness theorem, all we need to show is that each Q-DAG potential will evaluate to its corresponding probabilistic potential under all possible evidence. Formally, for any cluster and variables , the matrices of which are assigned to , we need to show that
 [IMAGE ]
for a given evidence . Once we establish this, we are guaranteed that will evaluate to the probability because the application of and in the Q-DAG algorithm is isomorphic to the application of * and + in the probabilistic algorithm, respectively.

To prove Equation 1, we will extend the Q-DAG node evaluator to mappings in the standard way. That is, if is a mapping from instantiations to Q-DAG nodes, then is defined as follows:

That is, we simply apply the Q-DAG node evaluator to the range of mapping .

Note that will then be equal to . Therefore,

Note also that by definition of , we have that equals . Therefore,

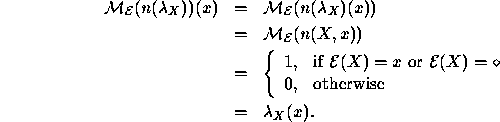
Therefore,