Appendix A: Ruling Out Ceiling Effects

 

For the data collected using a node limit, we examined all the problems in which at least one of the strategies hit the node limit. Table gives the second worst node count for all such problems. It shows that, for all the basic problems in which at least one strategy failed, and at least one other succeeded, the second-worst strategy generally created fewer than 7000 nodes.

Similarly, for the Trains and Tileworld problems, in all such cases except TW3, the second-worst strategy took fewer than 50,000 nodes (and in TW3 it took 89,790). Recall that the node limit for the basic problems was 10,000 nodes, while for the Trains and Tileworld problems it was 100,000 nodes. It is thus clear that the strategies that hit the node limit are doing substantially worse than the strategies that succeed. Even if they were to succeed by increasing the node limit slightly, their comparative performance would still be poor.

Thus, by using the node limits we imposed, we are not making any strategies look worse than they actually are. On the other hand, in computing %-overrun, we may be making some strategies look better than they actually are, because we use a value of 10,000 (or 100,000) nodes generated when a strategy hits the limit, and the actual number of nodes it might take, if run to completion, could be significantly higher. This is why, in our analyses, we considered both the absolute performance of strategies on individual problems, and their aggregate performance, as measured by average %-overrun.

  

Figure: Second-Worst Node Counts on Problems with Failing Strategies

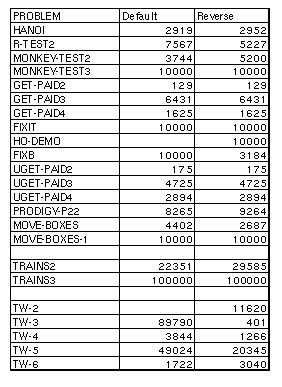
We also compared the experiments that were run with a time limit and those that were run with a node limit. For the basic problem set, the time limit of 100 seconds was high enough that, in most cases, strategies could compute significantly more nodes than they could with the node cutoff. Nonetheless, the results were almost identical. In nearly all cases, if a strategy failed with the node cutoff, it also failed with the time limit cutoff. There were only four exceptions to this:

1. Hanoi: With the 10,000 nodes limit, DSep fails, while with the 100 second time limit, it succeeds, taking 46,946 nodes.
2. Uget-Paid3: With the 10,000 node limit, UCPOP-LC fails, while with the 100 second time limit, it succeeds, taking 37,951 nodes.
3. Uget-Paid4: With the 10,000 node limit, UCPOP-LC fails, while with 100 second time limit, it succeeds, taking 23,885 nodes.
4. Fixit: With the 10,000 nodes limit, DSep-LC, UCPOP-LC, and ZLIFO fail, while with the 100 second time limit, they succeed in 12,732, 13,510, and 20,301 nodes respectively. All the other strategies fail to solve this problem under either limit.

There was a similarly strong correspondence between the results we obtained on the Trains and Tileworld problems using a node limit and a time limit. In a few cases, a strategy that was able to succeed within the 100,000 node limit was not able to succeed within the 1,000 second time limit. The nature of these problems is that the computation time per node can be very great. Specifically,

1. On TW3, DUnf succeeded in 56,296 nodes when run with a node limit, but failed with the 1,000 second time limit.
2. On TW4, LCFR-DSep (with an S+OC node-selection strategy) succeeded in 69,843 nodes, but failed on the time limit.
3. On TW5, LCFR-DSep (with an S+OC+UC node-selection strategy) succeeded in 49,024, but failed on the limit.
4. On TW6, LCFR (with an S+OC node-selection strategy) succeeded in 4,506 nodes, but failed with the time limit.

In only one case did a strategy fail under the node limit but succeed within the time limit:

1. On TW3, DSep (with an S+OC node-selection strategy) failed with a 100,000 node limit, but succeeded with 134,951 nodes using a 100 second time limit. Note that this is significantly worse than the second worst strategy, which solved this problem generating 89,790 nodes.

Given this close correspondence between the experiments with node and time limits, we collected only node-limit data for the experiments in which we reversed the precondition insertion.