Escaping from Local Minima

In Section 3.2 we defined the radius of a state as the shortest graph distance to a state with a better (lower) heuristic value. The radius affects the resources needed to find an escape route from a local minimum. There are several possible ways to escape from a local minimum. Exhaustive search methods, such as breadth-first search (BFS) or iterative deepening (ID), guarantee finding an escape route if such a route exists. However, an exhaustive search requires too much computation for any non-trivial escape task. We can try to make some use of the heuristic function by calling A* or IDA*. Both methods, however, waste much effort to ensure that the route to the goal state is optimal. We are looking for a search method that will find solutions quickly if the heuristic function is sufficiently accurate, but also guarantees finding a solution even if the heuristic function is poor.

Figure 5: The ILB algorithm

We came up with a search method that we call Iterative Limited BFS (ILB). The basic procedure is Limited BFS, which gets an initial state, a goal predicate, a breadth limit B and a depth limit⁵ D. It performs a BFS search to depth D. Whenever the number of nodes kept in memory exceeds B, it deletes the node with the worst heuristic value. This search is different from beam search. Limited BFS keeps the B best nodes of the current depth, while beam search keeps the B best nodes regardless of their depth. When B approaches infinity, beam search becomes best-first search, while limited BFS becomes BFS. ILB calls limited BFS iteratively until either a full BFS to depth D is performed or a solution is found. The breadth limit B is increased for each iteration and is set to the value k+bⁱ, where k is some constant, b is the maximum branching factor and i is the iteration number. This scheme guarantees that ILB will perform full BFS to depth D after D iterations. Figure 5 shows the algorithm. Note that this method is somewhat similar to iterative broadening [6], but there the broadening is performed at the node level. That means that for domains such as the sliding-tile puzzles which have a branching factor of less than 3, only 3 iterations would be performed.

Figure 6: An illustration of the way that ILB works. The state at the top is the local minimum. The state at the bottom left is a state with a lower (better) heuristic value. The states are ordered in levels according to their distance from the local minimum. In each level they are ordered by their heuristic value (the lowest value to the left). The gray states are the escape route. The gray rectangle shows the states visited in the last iteration of ILB. ILB will find the route when using a breadth limit of 4 and will require linear time (4 x 11) for its last iteration. ID will require exponential time for its last iteration (3¹¹ if the branching factor is 3).

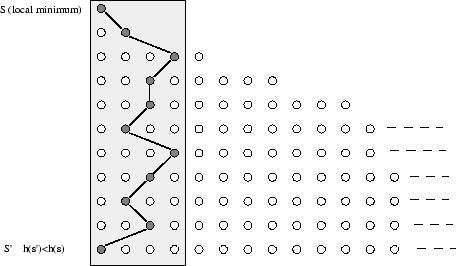Figure 6 illustrates the way that ILB works. The state at the top is the local minimum. The state at the left bottom is a state with a lower (better) heuristic value. The states are ordered in levels according to their distance from the local minimum. In each level they are ordered by their heuristic value (the lowest value to the left). The gray states are the escape route. ILB would find the route when using a breadth limit of 4 and will require linear time (4 x 11) for its last iteration. ID will require exponential time for its last iteration (3¹¹ if the branching factor is 3). The last iteration is dominant for both algorithms. Note that ILB works differently from iterative beam search. Beam search could progress to the right portion of the search graph instead of going deeper as ILB does.

The particular escape method is not an inherent part of MICRO-HILLARY. In the experimental section we will show that for the NxN puzzle domain, ILB is much faster than iterative deepening. In domains where the heuristic function does not indicate the direction of the escape route, ILB may reduce to full BFS and require too much memory. Furthermore, if $D \gg Length(Escape)$, ILB will also require much more computation time because all the iterations except the last one will be performed to depth D, while ID would search to a depth that is equal to the length of the escape route. In such cases, using iterative deepening as an escape algorithm may be more appropriate.

One important issue to consider when designing an escape procedure is whether acquired macros are used during the escape search. Using macros increases the branching factor, which can lead to a prohibitively expensive search, but it also allows deeper penetrations. In the experiments performed, we found that it is more beneficial to search for an escape route using only basic operators. It is quite possible, however, that in some domains it is beneficial to use macros.