Empirical Analysis

A second method of determining the comparative benefits of parallel search approaches is via empirical analyses. We have implemented a number of the approaches to parallel search described earlier in this paper in the EUREKA system. We have also constructed an artificial search space generator to provide a testbed for these experiments. Search space parameters can be established by the user, including:

• the cost of the optimal solution,
• the left-to-right position of the goal node in the space,
• the branching factor,
• the tree imbalance,
• the solution density (fraction of nodes at or beyond the optimal solution cost that represent goal nodes), and
• the heuristic error (the difference between the estimated and true distances to the nearest goal node).

All of the experiments described here were run on an nCUBE II message-passing multiprocessor using 32 processors.

  

Figure 7: Branching Factor and Optimal Number of Clusters

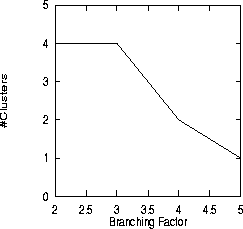
In our first experiment we consider how the optimal number of clusters may be affected by features of the problem space including branching factor, tree imbalance, and solution position. Figures 7, 8, and 9 demonstrate that the optimal number of clusters increases as the branching factor decreases (with a balanced tree, an optimal cost of 16, and the goal on the far right side of the tree), as the imbalance increases (with a branching factor of 3, an optimal cost of 15, and the goal in the middle of the tree), or as the goal node moves to the right side of the tree (with a balanced tree, a branching factor of 3, and an optimal cost of 15). In no case did one single number of clusters always perform best.

  

Figure 8: Tree Imbalance and Optimal Number of Clusters

  

Figure 9: Goal Position and Optimal Number of Clusters

In the next experiment we focus on the effects of operator ordering. Figure 10a demonstrates that employing operator ordering causes an increase in the optimal number of clusters, and Figure 10b shows that operator ordering (using perfect ordering information) results in a more significant improvement over no ordering as the solution node is positioned farther to the right in the tree. In this experiment the search trees are balanced with a branching factor of 4 and an optimal cost of 12. The dip in the plot occurs when the goal is positioned on the far left of a particular processor's subspace.

  

Figure 10: Ordering effects