The flexible roles defined in the CMUnited-97 software were an
improvement over the concept of rigid roles. Rather than associating
fixed ![]() coordinates with each position, an agent filling a
particular role was given a range of coordinates in which it could
position itself. Based on the ball's position on the field, the agent
would position itself so as to increase the likelihood of being useful
to the team in the future.
coordinates with each position, an agent filling a
particular role was given a range of coordinates in which it could
position itself. Based on the ball's position on the field, the agent
would position itself so as to increase the likelihood of being useful
to the team in the future.
However, by taking into account the positions of other agents as well as that of the ball, an even more informed positioning decision can be made. The idea of strategic position by attraction and repulsion (SPAR) is one of the novel contributions of the CMUnited-98 research which has been applied to both the simulator and the small robot teams [12].
When positioning itself using SPAR, the agent uses a multi-objective function with attraction and repulsion points subject to several constraints. To formalize this concept, we introduce the following variables:
SPAR extends similar approaches of using potential fields for highly dynamic, multi-agent domains [6]. The probability of collaboration in the robotic soccer domain is directly related to how ``open'' a position is to allow for a successful pass. Thus, SPAR maximizes the distance from other robots and minimizes the distance to the ball and to the goal, namely:
This formulation is a multiple-objective function. To solve this
optimization problem, we restate the problem as a single-objective
function. As each term may have a different relevance (e.g. staying
close to the goal may be more important than staying away from
opponents), we want to apply a different weighting function to each
term, namely ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , for opponents,
teammates, the ball, and the goal, respectively. Our anticipation
algorithm then maximizes a weighted single-objective function with
respect to P:
, for opponents,
teammates, the ball, and the goal, respectively. Our anticipation
algorithm then maximizes a weighted single-objective function with
respect to P:
![]()
In our case, we use ![]() ,
, ![]() , and
, and ![]() . For example, the last term of the objective function above
expands to
. For example, the last term of the objective function above
expands to ![]() .
.
One constraint in the simulator team relates to the position, or role, that the passive agent is playing relative to the position of the ball. The agent only considers locations that within one of the four rectangles, illustrated in Figure 5.4: the one closest to the position home of the position that it is currently playing. This constraint helps ensure that the player with the ball will have several different passing options in different parts of the field. In addition, players don't need to consider moving too far from their positions to support the ball.
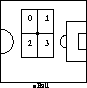
Figure 8: The four possible rectangles, each with one corner at the
ball's location, considered for positioning by simulator agents when
using SPAR.
Since this position-based constraint already encourages players to
stay near the ball, we set the ball-attraction weighting function
![]() to the constant function y=0. In addition to this first
constraint, the agents observe three additional constraints. In
total, the constraints in the simulator team are:
to the constant function y=0. In addition to this first
constraint, the agents observe three additional constraints. In
total, the constraints in the simulator team are:
This last constraint is evaluated by checking that there are no opponents in a cone with vertex at the ball and extending to the point in consideration.
In our implementation, the maximum of the objective function is estimated by sampling its values over a fine-grained mesh of points that satisfy the above constraints.
Using this SPAR algorithm, agents are able to anticipate the collaborative needs of their teammates by positioning themselves in such a way that the player with the ball would have several useful passing options.