To my knowledge, the work by Zhang and Dietterich [Zhang and Dietterich1995, Zhang1996] represents the only application of value function approximation to a combinatorial optimization problem. Since this work is the most closely related to what I propose to do, I will summarize it here in some detail while giving my own analysis of the issues involved.
Zhang and Dietterich attacked the problem of job-shop scheduling: given a partially-ordered set of jobs and the resources required by each, assign them start times so as to respect the partial order, meet constraints on simultaneous resource usage, and minimize the total execution time. Following the ``repair-based scheduling'' paradigm of [Zweben and Fox1994], they defined a search over the space of fully-specified schedules which meet the ordering constraints but not necessarily the resource constraints. Search begins at a fixed start state (the ``critical path schedule'') and proceeds by the application of two types of deterministic operators: REASSIGN-POOL and MOVE. To keep the number of instantiated operators small, they only considered operations which would repair the schedule's earliest constraint violation. Search terminates as soon as a violation-free schedule is reached.
The intent of Zhang and Dietterich's work was to learn a value
function which captured knowledge about not a single instance of a
scheduling problem, but rather a large family of related scheduling
instances. Thus, the input to their value function approximator (a
neural network) consisted of abstract problem-independent features,
such as the percentage of the schedule containing a violation and the
mean and standard deviation of certain slack times. Likewise, the
ultimate measure of schedule quality which the neural network was
learning to predict had to be normalized so that it spanned the same
range regardless of problem difficulty. These abstractions are
imperfect, since the true 
certainly differs from instance to
instance, and the abstracted problem features lack enough information
to actually produce the correct for any instance! Nevertheless,
if a reasonable instance-independent approximation can be learned, it
is beneficial because the cost of learning can be amortized
over the whole family of applicable problems.
In formulating a general combinatorial optimization problem as a
Markov decision problem, several issues arise. The first is that,
since only the quality of the final solution reached really matters,
and (unlike games) the search agent can choose to eventually reach any
state from any other state, the undiscounted value of every
state should be the same--an agent can eventually reach the global
optimum no matter what decision it makes. Figure 2
illustrates this issue on a trivial 5-state domain. Zhang and
Dietterich addressed this by adding a tiny penalty for each move; a
similar fix is to use a discount factor 
slightly less than 1.
Another possible solution, which allows undiscounted return to be used
safely, is to set an upper limit L on the number of steps in a
search trajectory. This gives rise to a second MDP formulation of the
optimization problem, where the number of steps remaining is included
in the state space as illustrated in Figure 3. Despite
the expanded state space, this alternative formulation is appealing:
smoother
and easier to approximate.
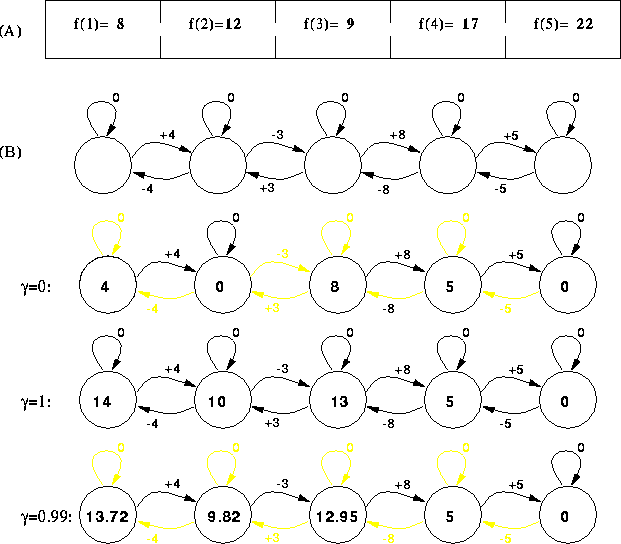
Figure: One formulation of combinatorial optimization as an MDP.
Part (A) shows a trivial 5-state domain with its objective
function f(x) and neighborhood relationship. The rewards of
the MDP (B) are constructed such that following a greedy
trajectory on the MDP is equivalent to hillclimbing on (A). The
lower three diagrams illustrate the optimal value function (bold
numbers) and policy (dark arrows) for different values of
. 
produces the greedy-hillclimbing policy;
produces a policy where all actions appear equally
good; 
produces a policy that leads directly to the
global optimum from all states.
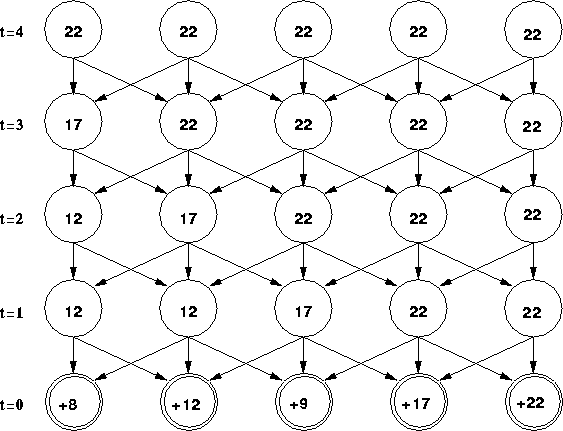
Figure 3: A second MDP formulation of the optimization problem.
The state space expands in order to keep track of the number of
steps remaining. All rewards are 0 except at the terminal
states. A state's value simply predicts the objective
function value of the best state that can be reached from x in
the amount of time remaining. Greedily following the
values (depicted) always leads to the globally optimal
.
One other issue should be noted. In optimization domains where each
state has hundreds or thousands of possible neighbors, choosing each
greedy action would involve significant computation time to evaluate
for each neighbor. A remedy for this is to make only a small
random subset of neighbors available from each state. In the extreme
case, a single random neighboring state y is chosen with probability
Pr(y|x), and the choice becomes simply whether to accept the move or
to stay put. With this change, the optimization process is no longer
deterministic nor strictly an MDP, but is still a generalized-MDP
[Littman and
Szepesvári1996] with associated Bellman equations:
This equation has the same form as the Bellman equation used in
Tesauro's backgammon experiments, where a position's value is defined
as an expectation (over dice rolls) of a max (over legal moves). And
as in the backgammon case, the TD( 
) algorithm may be used to learn
this value function with a neural network.
Following Tesauro's methodology, Zhang and Dietterich applied TD( ) to
the scheduling domain. Unlike backgammon, getting things to work
required substantial tuning. Experience replay [Lin1993], Gaussian
output representation [Pomerleau1991], exploration, and
loop-avoidance techniques all had to be carefully calibrated. They
trained the value function on a set of small problem instances.
Training continued until performance stopped improving on a validation
set of other problem instances. The N best-performing networks were
saved and used for the comparisons against Zweben's iterative-repair
system [Zweben and Fox1994], the previously best scheduler. The results
showed that searches with the learned evaluation functions produced
schedules as good as Zweben's in about half the CPU time.
My thesis will investigate two types of methods based on Value
Function Approximation for improving local search in combinatorial
optimization problems. One type, like Zhang and Dietterich's,
attempts to learn from scratch an approximate value function that can
steer a greedy search to a global optimum. I hope to extend Zhang and
Dietterich's framework to apply to other domains, using the
formulation described above, and to improve learning efficiency by
using ROUT in place of TD( ). The second type of VFA-based method, a
simpler approach, is based on predicting and then bootstrapping the
performance of a given search algorithm. My experiments to date have
centered on this latter approach, and I present those ideas in the
following section.
