The function 
is designed to reward states which are good
starting places for algorithm A. We can optimize 
using any
method; most straightforward is to apply the same graph-search
procedure as A, but to use instead of f as the evaluation
function. Whatever optimization procedure is chosen (call it B),
performing it should produce a state y which is a good starting
state for A; we can then run A starting from y to complete our
search. We use the notation ``B;A'' to represent this concatenation
of the two searches. Our ``STAGE'' algorithm, given in
Appendix A.3, interleaves function-approximator
training (by either batch fitting or TD( 
)) with running the two-stage
learned optimization procedure B;A.
The following example illustrates how STAGE can produce better
performance than the optimization method which it is learning about.
Consider minimizing the one-dimensional function 
over the domain X = [-10,10], as depicted in
Figure 4. Assuming a graph structure on this domain
where tiny moves to the left or right are allowed, hillclimbing
search clearly leads to a suboptimal local minimum for all but the
luckiest of starting points. However, the quality of the local minima
reached does correlate strongly with the starting position of x,
making it possible to learn useful predictions.
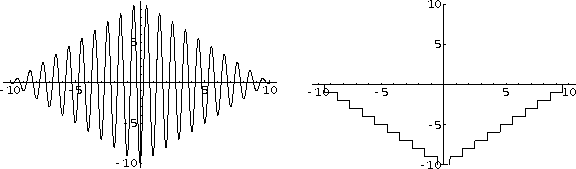
Figure 4: A one-dimensional function minimization domain (left) and the
value function which predicts hillclimbing's performance on that
domain (right). The value function is approximately linear in
the feature |x|. TD-learning easily identifies that
structure, resulting in an improved evaluation function for
guiding search to a global minimum.
We encode this problem for STAGE using a single input feature |x|,
which makes the value function approximately linear. Not
surprisingly, running STAGE with a linear function approximator
performs efficiently on this problem: after only a few trajectories
through the space, it learns 
. Hillclimbing on
rather than f(x), then, leads directly to the global
optimum.
This problem is contrived, but we think its essential property--that
features of the state help to predict the performance of an
optimizer--does indeed hold in many practical domains. We have
gotten excellent preliminary results in the domain of VLSI channel
routing. The learned evaluation function soundly outperforms the
hand-tuned function mentioned above in Equation 1
(page 
). Details of these results are given in
Appendix B.2.
Unlike the work of Zhang and Dietterich, which learns a search strategy from scratch using online value iteration, this method assumes an already-given search strategy for the domain and uses prediction to learn to improve on it. This simpler approach may serve as a better starting point for analysis.
My thesis will develop the STAGE algorithm further and apply it to the optimization domains of Section 5. One interesting direction for exploration is to apply STAGE recursively to itself, resulting in an automatically-generated multi-stage optimization algorithm. These stages, interleaving policy evaluation with execution, are reminiscent of the iterations of policy iteration, and my thesis will elaborate this relationship.