VFA in Acyclic Domains: ``ROUT''

 

I have presented two reasons why working strictly backwards may be desirable: efficiency, because updates need only be done on the ``frontier'' rather than all over state space; and robustness, because correct values, once assigned, need never again be changed. I have therefore investigated generalizations of the Dijkstra and DAG-SP algorithms specifically modified to accommodate huge state spaces and value function approximation. My variant of Dijkstra's algorithm, called Grow-Support, was presented in [Boyan and Moore1995] and will not be explored further in this thesis. My variant of DAG-SP is an algorithm called ROUT [Boyan and Moore1996], which this thesis will develop further.

In the huge domains for which ROUT is designed, DAG-SP's key preprocessing step--topologically sorting the entire state space--is no longer tractable. Instead, ROUT must expend some extra effort to identify states on the current frontier. Once identified (as described below), a frontier state is assigned its optimal value by a simple one-step backup, and this {state value} pair is added to a training set for a function approximator. Thus, ROUT's main loop consists of identifying a frontier state; determining its value; and retraining the approximator (see Appendix A.2). The training set, constructed adaptively, grows backwards from the goal.

ROUT's key subroutine, HUNTFRONTIERSTATE, is responsible for identifying a good state x to add to the training set. In particular:

1. All states reachable from x should already have their values correctly approximated by the function approximator. This ensures that the policy from x onward is optimal, and that a correct target value for can be assigned.
2. x itself should not already have its value correctly approximated. This condition aims to keep the training set as small as possible, by excluding states whose values are correct anyway thanks to good generalization.
3. x should be a state that we care to learn about. For that reason, ROUT considers only states which occur on trajectories emanating from a starting state of the MDP.

The HUNTFRONTIERSTATE operation returns a state which with high probability satisfies these properties. It begins with some state x and generates a number of trajectories from x, each time checking to see whether all states along the trajectory are self-consistent (i.e., satisfy Equation 4 to some tolerance ). If all states after x on all sample trajectories are self-consistent, then x is deemed ready, and ROUT will add x to its training set. If, on the other hand, a trajectory from x reveals any inconsistencies in the approximated value function, then we flag that trajectory's last such inconsistent state, and restart HUNTFRONTIERSTATE from there. Figure 2.3 illustrates how the routine works.

  
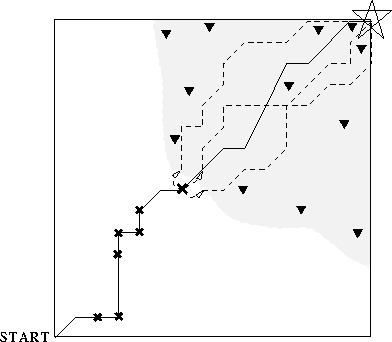
Figure 1: A schematic of ROUT working on an acyclic two-dimensional navigation domain, where the allowable actions are only , , and . Suppose that ROUT has thus far established training values for at the triangles, and that the function approximator has successfully generalized throughout the shaded region. Now, when HUNTFRONTIERSTATE generates a trajectory from the start state to termination (solid line), it finds that several states along that trajectory are inconsistent (marked by crosses). The last such cross becomes the new starting point for HUNTFRONTIERSTATE. From there, all trajectories generated (dashed lines) are fully self-consistent, so that state gets added to ROUT's training set. When the function approximator is re-trained, the shaded region of validity should grow, backwards from the goal.

The parameters of the ROUT algorithm are H, the number of trajectories generated to certify a state's readiness, and , the tolerated Bellman residual. ROUT's convergence to the optimal , assuming the function approximator can fit the training set perfectly, can be guaranteed in the limiting case where (assuring exploration of all states reachable from x) and . In practice, of course, we want to be tolerant of some approximation error. Typical settings I used were H=20 and roughly 5% of the range of ).

In experiments on two medium-sized domains ( states), ROUT learned evaluation functions which were as good or better than those learned by TD( ) with the same neural-net approximator, and used an order of magnitude less training data to do so. These results are detailed in Appendix B.1.

When a function approximator is capable of fitting , ROUT will, in the limit, find it. However, for ROUT to be efficient, the frontier must grow backward from the goal quickly, and this depends on good extrapolation from the training set. When good extrapolation does not occur, ROUT may become stuck, repeatedly adding points near the goal region and never progressing backwards. Some function approximators may be especially well-suited to ROUT's required extrapolation from accurate training data, and I plan to explore this. I will also explore algorithmic refinements to make ROUT more robust in general. One such refinement is to adapt the tolerance level , thereby guaranteeing progress at the expense of accuracy.

With such improvements, I hope to develop ROUT into the algorithm of choice for learning evaluation functions for large-scale acyclic domains. I will validate it empirically on the control problem of factory scheduling (Section 5.3), the game of backgammon, and a variety of combinatorial optimization problems formulated as acyclic MDPs as described below.