The field can be expressed as

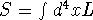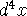where L is the lagrangian density. Action should be a lorentz scalar if this equation is to apply in all reference frames. Since is lorentz invariant, this means 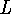should be lorentz invariant.

1. Easiest L: 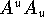problem: changes with gauge transformations. L should be gauge invariant. 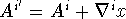and 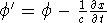gives same electric and magnetic field. More simple expressed, this is: .
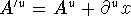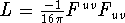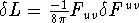2. Next L: use field strength tensor so 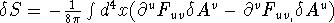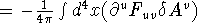so so 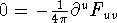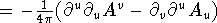. The lorentz gauge gives: so 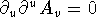. This is just the wave equation.
3. With a charge or current, 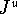, assume 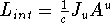. Then 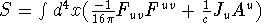so 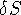which gives: 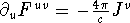. Expanding into space and time, you get: 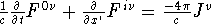. This equation splits into: 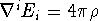and 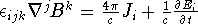. The other 2 maxwell's equations are automatically satisfied using the dual tensor.

source psfile jl@crush.caltech.edu index