Algoritmi

Mihai Budiu -- mihaib+@cs.cmu.edu, http://www.cs.cmu.edu/~mihaib/

1 iunie 1997

Subiect:: Noi direcţii în cercetări legate de algoritmi
Cunoştinţe necesare:: Cunoştinţe elementare despre algoritmi, analiză matematică elementară, teoria grafurilor
Cuvinte cheie:: algoritm, invariant, complexitate, aproximaţie, aleator, on-line.

Algoritmi; complexitate
Algoritmi aproximativi
Algoritmi Monte Carlo
Algoritmi Las Vegas
- Rădăcinile unui polinom
- Izomorfismul arborilor
Algoritmi on-line
- Problema schiorului
Rezumat

În ultimii ani cercetarea în domeniul algoritmilor a apucat pe nişte căi extrem de interesante şi foarte deosebite de cele tradiţionale. Unele dintre aceste căi erau prefigurate de descoperiri făcute cu multă vreme în urmă, dar nu fuseseră urmate sistematic. Altele sunt de dată recentă. Metodele noi încearcă să depăşească criza în care intraseră metodele de rezolvare a anumitor clase de probleme (cum ar fi cele NP-complete), sau să facă faţă unor probleme de naturi diferită: informaţie incompletă (de exemplu cînd trebuie luate decizii fără a cunoaşte cererile ulterioare), informaţie distribuită (într-o reţea de calculatoare), informaţie ascunsă (în criptografie), etc. Acest articol îşi propune să ilustreze foarte sumar cîteva dintre noile direcţii de acţiune.

Algoritmi; complexitate

În această secţiune vom face o scurtă recapitulare a principalelor noţiuni care ne sunt necesare în înţelegerea celorlalte părţi. Acestea sunt bine-cunoscute din studiul algoritmilor clasici, astfel încît cititorul informat le poate sări fără pierderi de informaţie. Tratarea va fi desigur sumară; cititorul ne-informat este invitat să parcurgă cărţi clasice în domeniu pentru o discuţie mai amplă. Pe de altă parte aceste noţiuni nu sunt simple, şi foarte arar sunt tratate într-adevăr riguros. Deşi expunerea de faţă va fi sumară, sper că nu va păcătui şi prin lipsă de corectitudine.

Limbajul de descriere

Un algoritm este o descriere a unui proces de calcul, care din nişte date iniţiale produce nişte rezultate interesante. Descrierea se face în termenii unor operaţii elementare (operaţii aritmetice, comparaţii, decizii, etc.).

Aparent modul în care rezolvăm problemele depinde de operaţiile pe care le avem la-ndemînă. În cazul acesta se iveşte natural întrebarea dacă anumite operaţii nu sunt mai expresive decît altele. Acest lucru este adevărat, după cum se vede şi din proliferarea limbajelor de programare; un astfel de limbaj defineşte practic o colecţie de operaţii elementare.

Se poate demonstra absolut riguros, că în oarecare măsură alegerea limbajului este irelevantă, pentru că, din momentul în care avem un limbaj suficient de expresiv, putem simula cu ajutorul lui operaţiile care se fac în toate celelalte limbaje cunoscute. Astfel, toate formalismele care exprimă procese de calcul au fost demonstrate ca fiind echivalente ca putere expresivă (limbajele de programare, lambda calculul, funcţiile recursive, gramaticile de tip 0, maşinile Turing: toate aceste metode de calcul pînă la urmă sunt echivalente).

Din acest motiv ne putem fixa asupra unui limbaj anume, fără a pierde nimic din generalitatea expunerii. Voi folosi pentru exemplele din acest articol un limbaj foarte simplu, asemănător cu limbajele obişnuite de programare. Limbajul (``guarded command language'') a fost introdus de Dijkstra, şi se bazează pe folosirea gărzilor, care sunt nişte simple expresii booleene. Gărzile sunt folosite pentru a descrie două construcţii: bucla do şi instrucţiunea if. Astfel:

do garda_1 -> instructiune_1
[] garda_2 -> instructiune_2
...
[] garda_n -> instructiune_n
od

funcţionează astfel: gărzile se evaluează; dacă:

toate sunt false, atunci ciclul do se termină.
dacă cel puţin o gardă este adevărată, atunci instrucţiunea corespunzătoare se execută, după care bucla se reia.
în caz că mai multe gărzi sunt adevărate, atunci una dintre instrucţiuni se va executa, dar care, nu se ştie.

Dacă programatorul vrea să fie sigur ce instrucţiune se execută, nu are decît să construiască programul în aşa fel încît două gărzi sa nu fie adevărate simultan.

Construcţia do este asemănătoare cu un while urmat de un switch din C, dar este mai uşor de folosit. Oricum, este evident că este la fel de expresivă.

Folosim apoi construcţia if pe post de switch (case din Pascal):

if garda_1 -> instructiune_1
[] garda_2 -> instructiune_2
...
[] garda_n -> instructiune_n
fi

Semnificaţia este foarte asemănătoare cu a lui do. Astfel:

Dacă nici o gardă nu este adevărată programul se termină imediat (eroare);
Dacă o gardă este adevărată instrucţiunea corespunzătoare se execută;
Cînd mai multe gărzi sunt adevărate, una dintre instrucţiunile care le corespund este executată, dar nu se precizează care.

Mai folosim şi atribuirea paralelă:

v_1, v_2, ..., v_n := e_1, e_2, ..., e_n

Prin care expresiile din dreapta sunt toate evaluate şi atribuite simultan variabilelor din stînga. Din cauza asta schimbul valorilor a două variabile se poate face cu

x, y := y, x

care operaţie nu este echivalentă nici cu

x := y 
y := x

şi nici cu

y := x
x := y

Un exemplu

Ca să ne familiarizăm cu limbajul, să scriem un mic algoritm, care, dîndu-se o valoare x şi un vector a cu n elemente, partiţionează vectorul în aşa fel încît valorile mai mici ca x ajung în stînga, cele mai mari în dreapta, iar toate cele egale cu x sunt contigue, undeva între celelalte două (acesta este un fragment din quicksort):

l, r, m := 1, n, 1
do a[m] = x -> m := m+1
[] a[m] < x -> a[l], a[m], l, m := a[m], a[l], l+1, m+1
[] (a[m] > x) and (m < r) -> a[r], a[m], r := a[m], a[r], r-1
[] a[r] > x -> r := r-1
od

Acest algoritm operează asupra vectorului a menţinînd următorul invariant (o relaţie care este întotdeauna adevărată):

|     <     |        =      |         ?       |      >    | a
-----------------------------------------------------------
 1           ^               ^                 ^         n
             l               m                 r

Variabilele l, m şi r sunt indici în vectorul a. Tot ce e la stînga lui l e mai mic decît x, tot ce este cuprins între l (inclusiv) şi m (exclusiv) este egal cu x, iar tot ce se află la dreapta lui r este mai mare ca x. Elementele dintre m şi r sunt încă ne-explorate. Această relaţie este adevărată atunci cînd algoritmul începe, din modul în care se iniţializează variabilele, şi rămîne adevărată la fiecare parcurgere a buclei do, după cum se poate verifica. Bucla se termină cînd toate gărzile sunt adevărate, ceea ce se poate doar dacă m = r, deci dacă zona ne-explorată s-a redus la 0.

Limbajul acesta nu este foarte eficace pentru a scrie sisteme de operare, dar pentru a exprima algoritmi este foarte succint şi elegant. Invariantul anterior se reduce, în cazul terminării, deci cînd m = r la

|     <          |        =         |      >              | a
-----------------------------------------------------------
 1                ^                  ^                   n
                  l                  m=r

ceea ce implică şi corectitudinea algoritmului, pentru că acesta este rezultatul pe care trebuia să-l obţinem.

Ca să demonstrăm ca algoritmul se termină întotdeauna, independent de valorile lui x, n şi a, observaţi că ori toate gărzile sunt false (şi atunci gata), ori cel puţin o gardă este adevărată, şi atunci fie m creşte, fie r scade. Cum întotdeauna trebuie să avem m < r, bucla se poate parcurge de cel mult n ori înainte de terminare.

Observaţi că acest algoritm este nedeterminist, pentru că dacă a[r] > x poate face două alegeri. Interesant este că rezultatul final nu depinde de care operaţie este făcută, pentru că ambele operaţii păstrează invariantul indicat şi reprezintă un progres. De asemenea, observaţi că algoritmul rămîne corect dacă eliminăm ultima linie din do, şi în acest caz devine şi determinist!

Instanţe şi probleme

O distincţie foarte importantă pe care trebuie s-o facem este între clasa de probleme pe care o rezolvă un algoritm, şi instanţele specifice ale acelei probleme. De exemplu, algoritmul descris mai sus rezolva toate problemele care conţin un vector de n elemente şi o valoare x, aducînd vectorul la forma indicată. Cînd rulăm acest algoritm însă, o facem cu o instanţă particulară a problemei: de exemplu vectorul cu n=5 elemente a = [1, 2, 5, 3, 2], şi cu x = 2.

Distincţia este esenţială, mai ales cînd vrem să evaluăm eficacitatea unui algoritm. Măsurarea performanţei unui algoritm cu ceasul în mînă nu este o operaţie foarte semnificativă, dacă algoritmul va rezolva şi alte instanţe ale problemei decît cea măsurată. Dacă algoritmul de mai sus, implementat pe un anumit calculator, rezolvă instanţa indicată în 5 milisecunde, asta nu spune absolut nimic despre viteza lui pentru o cu totul altă instanţă. Dacă vrem să evaluăm calitatea algoritmilor trebuie să găsim o metodă care nu depinde de instanţe, ci de problema însăşi.

Complexitate asimptotică

O întrebare pe care ne-o putem imediat pune este: cît de bun este un algoritm? Nu se poate scrie un altul mai bun (care să rezolve aceeaşi problemă, fireşte)? Pentru a putea răspunde, trebuie să cădem de acord asupra unei metode prin care măsurăm calităţile unui algoritm; putem măsura timpul lui de execuţie pentru o anumită problemă, sau cantitatea de memorie folosită, sau numărul de instrucţiuni care descriu programul, sau poate o altă dimensiune.

Dacă am doi algoritmi pentru aceeaşi problemă, atunci poate pentru anumite instanţe ale problemei unul este mai rapid, iar pentru alte instanţe celălalt. Dintre algoritmii de sortare sortarea prin selecţie este preferată pentru vectori mici, iar quicksort sau heapsort pentru vectori mari. Dacă valorile din vector sunt mici, atunci le bate pe amîndouă radixsort. Şi atunci, cum comparăm doi algoritmi?

Există un răspuns relativ unanim acceptat la această întrebare, dar, înainte de a-l prezenta, trebuie încă odată să spunem că acesta este doar un punct de vedere în comparaţie, şi că în practică se pot prefera algoritmii şi din alte motive. Cel mai interesant atribut al performanţei a fost judecat a fi timpul de execuţie al unui algoritm. Timpul este apoi asimilat cu numărul de operaţii elementare pe care le efectuează un algoritm pentru a rezolva o problemă.

Din păcate, chiar pentru o instanţă fixată a unei probleme, numărarea instrucţiunilor executate este o sarcină foarte dificilă. Din această cauză se socoteşte suficient a se măsura de cîte ori se repetă instrucţiunea care se execută cel mai mult. Aceasta este instrucţiunea dominantă, şi se găseşte de regulă în interiorul tuturor buclelor. Numărul de repetiţii al instrucţiunii dominante este o aproximaţie rezonabilă pentru numărul total de instrucţiuni executat de algoritm. Oricum, din moment ce nici o instrucţiune nu se mai execută atît de mult, dacă înmulţim lungimea programului cu numărul de repetiţii al instrucţiunii dominante avem imediat o margine superioară pentru timpul de execuţie. Vom vedea mai jos că folosirea pentru a indica complexitatea a ordinului de mărime a unei funcţii face neimportant un factor multiplicativ (anume lungimea programului).

Observaţi că pentru instanţe diferite ale unei aceleiaşi probleme, numărul de instrucţiuni executat este în general diferit. De exemplu, acest scurt program, care caută un număr x în vectorul a:

i = 1
do (i <= n) and not (a[i] = x) -> i := i + 1
od

va avea un timp de execuţie egal cu 1 dacă x = a[1] sau cu n dacă x nici nu apare în vector.

Este de asemenea evident că timpul de execuţie depinde adesea de cantitatea datelor de intrare; în exemplele date mai sus el depinde de numărul de elemente din vectorul a.

Să recapitulăm deci: avem un algoritm care rezolvă o clasă de probleme. Pentru fiecare instanţă, complexitatea algoritmului se măsoară în numărul de instrucţiuni executate pentru a rezolva acea instanţă.

Noi ne dorim însă o măsură unică, globală a unui algoritm, care să-l caracterizeze, şi nu complexitatea pentru fiecare instanţă. Atunci procedăm astfel: alegem o valoare arbitrară care o numim mărimea datelor de intrare. Cînd algoritmul lucrează pe un vector (ca în exemplul de mai sus), o alegere posibilă este numărul de elemente. În general valoarea care caracterizează mărimea datelor de intrare arată cît de multă informaţie este prezentă în datele de intrare. Acesta este un lucru normal, pentru că ne putem aştepta ca atunci cînd avem mai multe date la intrare algoritmul să lucreze mai multă vreme.

În acest fel partiţionăm mulţimea intrărilor în mulţimi (disjuncte) de ``mărimi'' egale. Pentru algoritmul precedent vom avea astfel probleme de ``mărime 1'': cele care au vectorul dintr-un singur element. Vom avea probleme de ``mărime k'', cu vectori de lungime k, ş.a.m.d. Fireşte, există mai multe instanţe cu mărimea k.

Mai departe există două metode răspîndite pentru a decide complexitatea unui algoritm pentru date de mărime fixată. Cea mai comună se cheamă: ``cel mai rău caz'' (worst-case complexity). Pe scurt: fixăm mărimea, măsurăm numărul de instrucţiuni pentru fiecare instanţă de această mărime, şi apoi luăm maximumul.

T(n) = max_{marime(P) = n} timp(P)

Complexitatea T pentru mărimea fixată n este maximumul timpilor pentru toate problemele de mărime n.

De exemplu, pentru algoritmul de căutare expus mai sus, complexitatea pentru vectori de mărime n este n, pentru instanţele în care x nu se regăseşte în vector.

În acest fel complexitatea unei probleme se exprimă ca o funcţie de mărimea problemei.

   date de intrare P
------------------------
| instante de marime 1 |     -> max timp(P) = T(1)
------------------------ 
| instante de marime 2 |     -> max timp(P) = T(2)    
------------------------
....
------------------------
| instante de marime n |     -> max timp(P) = T(n)
------------------------
....

A doua metodă de a evalua complexitatea problemelor pentru o mărime fixată este de a pune o distribuţie de probabilitate peste instanţele de o anumită mărime (de exemplu toate pot fi egal probabile) şi de a evalua apoi valoarea medie a variabilei aleatoare care descrie timpul de rulare. Considerînd numai problemele de mărime n, dacă rezolvarea problemei x va dura un timp t(x) iar problema se va ivi cu probabilitatea p(x), atunci complexitatea algoritmului va fi

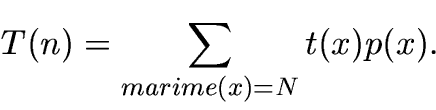
$\begin{displaymath}T(n) = \sum_{marime(x) = N} t(x) p(x).\end{displaymath}$

O astfel de evaluare se numeşte ``cazul mediu'': ``average case complexity''.

Această tehnică este mult mai rar folosită, pentru că:

Este greu de argumentat o distribuţie de probabilitate pentru un set de date de intrare (practic distribuţia afirmă ce şansă are fiecare instanţă de a fi întîlnită cînd se rulează algoritmul). De exemplu, pentru un algoritm pe grafuri, care este probabilitatea de a primi un arbore? Nu există un răspuns natural la această întrebare.
În general este mult mai greu de evaluat analitic formula obţinută decît în cazul folosirii maximumului.

Metoda cu distribuţia de probabilitate a fost în general aplicată la algoritmi de căutare şi sortare, dar chiar şi în aceste cazuri simple rezultatele nu sunt întotdeauna facile.

De aici înainte vom presupune că folosim complexitate ``worst case''.

Cînd cineva spune ``acesta este un algoritm de complexitate n², de fapt vrea să spună: ``pentru anumite de intrare de mărime n algoritmul execută instrucţiunea dominantă de cel mult n² ori.'' Acest n este implicit deci dimensiunea datelor de intrare. Vom folosi şi noi această literă liber, fără a mai indica sursa ei de provenienţă.

Simbolul lui Landau

Pentru că de fapt noi socotim numai numărul de repetiţii al instrucţiunii dominante, şi nu toate instrucţiunile executate, nu are foarte mult sens să comparăm între un algoritm cu complexitatea n şi unul cu complexitate n+1. Toate instrucţiunile care nu au fost măsurate au o contribuţie care să facă algoritmul cu n să dureze în realitate mai mult decît cel cu n+1. Ceea ce trebuie să comparăm de fapt este ordinul de mărime al complexităţii, care pune în evidenţă creşteri substanţial diferite. Pentru a face evident acest lucru se foloseşte o notaţie pentru ordinul de mărime al unei funcţii, introdus de fizicianul Lev Davidovich Landau. Notaţia foloseşte simbolul O (``o mare'') pentru a indica mulţimea funcţiilor care cresc mai repede decît o funcţie dată. Această notaţie compară numai funcţii la limită, în creşterea lor spre infinit. Pentru a putea compara complexitatea a doi algoritmi care rezolvă o aceeaşi problemă în acest fel, trebuie ca ei să poată lucra cu probleme de mărimi arbitrar de mari!

Definiţie: fie dată o funcţie f : N --> N, astfel încît de la un rang încolo f(n) > 0; atunci mulţimea funcţiilor dominate de f se notează cu O(f) şi se defineşte astfel:

În cuvinte, o funcţie este în mulţimea O(f) dacă la ``creşte mai încet'' decît f la infinit. De exemplu, funcţia g(n) = n este în mulţimea O(n²), pentru că $g(n)/n^2 \rightarrow 0$ . În general, un polinom de grad mai mic decit k este în mulţimea O(n^k).

Din păcate notaţia se foloseşte în uzajul comun în mod greşit, scriindu-se f = O(g) în loc de $f \in O(g)$ : O(g) este o mulţime de funcţii, toate dominate de g.

Din considerentele indicate, metoda preferată pentru a indica complexitatea unui algoritm este de a o face prin ordinul de mărime al funcţiei sale de complexitate. Din cauza că analizează această comportare spre infinit complexitatea algoritmilor se numeşte ``complexitate asimptotică''.

Ce înseamnă deci că un algoritm ``are o complexitate O(n log n)''? Înseamnă că pe măsură ce datele de intrare cresc în mărime ca n, numărul de operaţii făcut de algoritm în raport cu mărimea datelor de intrare este mai mică de n log n ori.

Astfel complexitatea asimptotică exprimă concis o limită superioară a timpului de execuţie a unui algoritm. O grămadă de informaţie se pierde din descrierea complexităţii unui algoritm dînd numai ordinul de mărime:

În primul rînd funcţia al cărei ordin de mărime este evaluată era obţinută luînd maximumul peste toate instanţele de o anumită mărime.
În al doilea rînd, dacă $f \in O(g)$ asta înseamnă numai că de la un rang încolo f e ``mai mică'' decît g; rangul acesta ar putea foarte bine fi mai mare decît numărul de atomi din univers, deci mai mare decît al oricărei probleme practice pe care vrem s-o rezolvăm.
Notaţia cu O indică numai limita superioară a unei funcţii; observaţi că atît $f(n) = n \in O(n^2)$ cît şi $g(n) = n^2 \in O(n^2)$ . Numai informaţia că f şi g sunt în aceeaşi clasă nu ne permite de fapt să le comparăm între ele. Pentru a indica şi faptul că limita se atinge, se foloseşte o altă notaţie, cu $\Omega$ ¹. De exemplu, dacă ştiu despre un algoritm doar că este O(n², asta spune ceva. Dar dacă mi se spune şi că există o serie de instanţe, crescătoare în mărime, pe care algoritmul face c n² + ..., atunci ştiu mult mai mult; ştiu de exemplu că algoritmul este ``mai prost'' decît un algoritm O(n), iar complexitatea lui poate fi indicată cu semnul $\Omega(n^2)$ .

Cu toate aceste dezavantaje, notaţia cu O s-a impus, şi s-a dovedit în general destul de eficace pentru a caracteriza algoritmii. Proprietăţile notaţiei O sunt foarte interesante, dar depăşesc cadrul acestui articol; în general sunt destul de intuitive (de exemplu: dacă f = O(g) şi g = O(h), atunci f = O(h)$, etc.

În final, reluînd o observaţie de la începutul secţiunii, să observăm că într-adevăr n = O(n+1) şi n+1 = O(n), aşa că într-adevăr notaţia cu O aruncă termenii nesemnificativi, şi faptul că am numărat numai instrucţiuni dominante nu are nici o importanţă. Mai exact, este foarte uşor de arătat că timpul real de execuţie a unui algoritm este O(numărul de repetiţii al instrucţiunii dominante).

Complexitatea revizuită

Am admis tacit că toate operaţiile elementare se pot efectua în timp unitar, dar acest lucru poate adesea să ne inducă în eroare. De exemplu, atunci următorul algoritm, care calculează numărul 2^{2^...²}, funcţionează în n paşi:

x, i := 2, 1
do i <= n -> x, i := x * x, i+1
od

Numărul care se obţine în acest fel este extrem de lung, şi este mult mai rezonabil să presupunem că operaţiile cu numere iau un timp care depinde de lungimea numărului în biţi.

Vom ignora însă aceste considerente uşor ezoterice, şi ne vom mulţumi să presupunem că în algoritmii noştri toate operaţiile pot fi făcute în timp constant.

Complexitatea unei probleme

Un algoritm rezolvă o problemă. Adesea pentru a rezolva o aceeaşi problemă putem folosi mai mulţi algoritmi, poate cu complexităţi diferite. Există cel puţin 30 de metode de a sorta un şir de valori, de exemplu! Putem vorbi deci de complexitatea unui algoritm, dar şi de complexitatea unei probleme. Complexitatea unei probleme este complexitatea celui mai ``rapid'' algoritm care o poate rezolva. Complexitatea unei probleme este deci o limită inferioară a eficacităţii cu care putem rezolva o problemă: orice algoritm care va rezolva acea problemă va fi mai complex decît complexitatea problemei.

În general este extrem de dificil de evaluat complexitatea unei probleme, pentru că rareori putem demonstra că un algoritm este cel mai bun posibil. Tabloul arată cam aşa:

limita inferioara          complexitatea          cel mai bun 
      dovedita             problemei              algoritm cunoscut
---------|------------------?----------------------|----------------
         f                                         g

Cu alte cuvinte, putem spune: ``problema asta nu se poate face mai repede de f, şi noi ştim s-o rezolvăm în g''. Dar care este complexitatea reală, şi care este algoritmul care rezolvă problema optim, asta foarte rar se poate spune.

Pentru o problemă atît de banală ca înmulţirea a două numere, considerînd numerele scrise în baza 2, iar mărimea lor numărul total de biţi n, complexitatea celui mai bun algoritm de înmulţire cunoscut este de O(n log n log log n), dar limita inferioară dovedită este de n. Sau pentru înmulţirea a două matrici de n*n elemente: se găsesc încontinuu algoritmi din ce în ce mai buni (asimptotic vorbind), dar limita inferioară de n² este încă departe de cel mai bun (şi foarte sofisticat algoritm), care este aproximativ O(n^2,3) (comparaţi cu algoritmul ``naiv'' imediat, care este O(n³)).

Clasa P; alte clase deterministe

Unele probleme se pot rezolva, altele nu. De exemplu, o problemă notorie, a cărei imposibilitate este riguros demonstrată în anii '30 de către matematicianul englez Alan Turing, este de a decide dacă un program se va opri vreodată pentru o anumită instanţă a datelor de intrare.

Pe de altă parte, chiar între problemele care pot fi rezolvate, teoreticienii trag o linie imaginară între problemele care au rezolvări ``rezonabil'' de rapide, şi restul problemelor, care se numesc ``intratabile''.

În mod arbitrar, dar nu ne-justificabil, o problemă se numeşte ``intratabilă'' dacă complexitatea ei este exponenţială în mărimea datelor de intrare. (Nu uitaţi, este vorba de complexitate ``worst-case'' asimptotică.) O problemă este ``tratabilă'' dacă putem scrie complexitatea ei sub forma unui polinom, de un grad oricît de mare.

Mulţimea tuturor problemelor de decizie (adică a problemelor la care răspunsul este da sau nu) cu complexitate polinomială se notează cu P (de la polinom). De exemplu, problema de a găsi dacă o valoare se află într-un vector este în clasa P; algoritmul exhibat mai sus este un algoritm în timp linear (O(n)) pentru a răspunde la această întrebare.

Un exemplu de problemă cu complexitate exponenţială (ne-polinomială)? Iată unul: dacă se dă o formulă logică peste numerele reale, cu cuantificatori existenţiali ( $\exists$ ) şi universali ( $\forall$ ), care foloseşte numai operaţii de adunare, comparaţii cu < şi conectori logici ( $\land, \lor, \Rightarrow, \ldots$ ), este formula adevărată? (Un exemplu de formulă: `` $\forall x \exists y \forall z \; (x + z < y) \land (2x - z > y)$ ''). Decizia se poate face numai într-un timp exponenţial în lungimea formulei (pentru anumite instanţe), dar demonstraţia nu este de loc simplă.

(Ca o curiozitate: există şi probleme cu o complexitate ``ne-elementară'', care este mai mare decît complexitatea oricărei probleme exponenţiale. O astfel de problemă este cea de decizie a adevărului unei formule în teoria numită S1S, sau ``teoria monadică a succesorilor de ordinul 2''. Nu vă lăsaţi intimidaţi de terminologie: aceasta este practic o teorie logică peste numerele naturale, în care avem voie să scriem formule cu cuantificatori şi conectori logici, ca mai sus, dar avem şi dreptul să cuantificăm peste mulţimi. Complexitatea deciziei unei formule logice într-o astfel de teorie este mai mare decît $\underbrace{2^{2^{\ldots^n}}}_k$ pentru orice k natural!)

Clasa NP; algoritmi nedeterminişti; NP-completitudine

Algoritmii cu care suntem obişnuiţi să lucrăm zi de zi sunt determinişti. Asta înseamnă că la un moment dat evoluţia algoritmului este unic determinată, şi ca instrucţiunea care urmează să se execute este unic precizată în fiecare moment. Am văzut însă că limbajul pe care l-am folosit ne permite scrierea unor algoritmi care au mai multe posibilităţi la un moment dat; construcţia if din limbajul cu gărzi permite evaluarea oricărei instrucţiuni care are garda adevărată.

Acest tip de algoritmi este surprinzător de bogat în consecinţe cu valoare teoretică. Aceşti algoritmi nu sunt direct aplicabili, însă studiul lor dă naştere unor concepte foarte importante.

Surprinzătoare este şi definiţia corectitudinii unui astfel de algoritm. Un algoritm nedeterminist este corect dacă există o posibilitate de executare a sa care găseşte răspunsul corect. Pe măsură ce un algoritm nedeterminist se execută, la anumiţi paşi se confruntă cu alegeri nedeterministe. Ei bine, dacă la fiecare pas există o alegere, care făcută să ducă la găsirea soluţiei, atunci algoritmul este numit corect.

Astfel, un algoritm nedeterminist care caută ieşirea dintr-un labirint ar arăta cam aşa:

do not iesire(pozitie_curenta) ->
    if not perete(nord(pozitie_curenta)) -> 
            pozitie_curenta := nord(pozitie_curenta)
    [] not perete(est(pozitie_curenta)) -> 
            pozitie_curenta := est(pozitie_curenta)
    [] not perete(sud(pozitie_curenta)) -> 
            pozitie_curenta := sud(pozitie_curenta)
    [] not perete(vest(pozitie_curenta)) -> 
            pozitie_curenta := vest(pozitie_curenta)
    fi
od

Pe scurt algoritmul se comportă aşa: dacă la nord nu e perete mergi încolo, sau, poate, dacă la sud e liber, mergi încolo, sau la est, sau la vest. În care dintre direcţii, nu se precizează (este ne-determinat). Este clar că dacă există o ieşire la care se poate ajunge, există şi o suită de aplicări ale acestor reguli care duce la ieşire.

Utilitatea practică a unui astfel de algoritm nu este imediat aparentă: în definitiv pare să nu spună nimic util: soluţia este fie spre sud, fie spre nord, fie spre este, fie spre vest. Ei şi? Este clar că aceşti algoritmi nu sunt direct implementabili pe un calculator real.

În realitate existenţa un astfel de algoritm deja înseamnă destul de mult. Înseamnă în primul rînd că problema se poate rezolva algoritmic; vă reamintesc că există probleme care nu se pot rezolva deloc.

În al doilea rînd, se poate arăta că fiecare algoritm nedeterminist se poate transforma într-unul determinist într-un mod automat. Deci de îndată ce ştim să rezolvăm o problemă într-un mod nedeterminist, putem să o rezolvăm şi determinist! Transformarea este relativ simplă: încercăm să mergem pe toate drumurile posibile în paralel, pe fiecare cîte un pas. (O astfel de tehnică aplicată în cazul labirintului se transformă în ceea ce se cheamă ``flood fill'': evoluez radial de la poziţia de plecare în toate direcţiile).

Clasa tuturor problemelor care se pot rezolva cu algoritmi nedeterminişti într-un timp polinomial se notează cu NP (Nedeterminist Polinomial). Este clar că orice problemă care se află în P se află şi în NP, pentru că algoritmii determinişti sunt doar un caz extrem al celor determinişti: în fiecare moment au o singură alegere posibilă.

Din păcate transformarea într-un algoritm determinist se face pierzînd din eficienţă. În general un algoritm care operează în timp nedeterminist polinomial (NP) poate fi transformat cu uşurinţă într-un algoritm care merge în timp exponenţial (EXP). Avem deci o incluziune de mulţimi între problemele de decizie: P $\subseteq$ NP $\subseteq$ EXP.

Partea cea mai interesantă este următoarea: ştim cu certitudine că P $\not=$ EXP. Însă nu avem nici o idee despre relaţia de egalitate între NP şi P sau între NP şi EXP. Nu există nici o demonstraţie care să infirme că problemele din NP au algoritmi eficienţi, determinist polinomiali! Problema P=NP este cea mai importantă problemă din teoria calculatoarelor, pentru că de soluţionarea ei se leagă o grămadă de consecinţe importante.

Problema aceasta este extrem de importantă pentru întreaga matematică, pentru că însăşi demonstrarea teoremelor este un proces care încearcă să verifice algoritmic o formulă logică (cum am văzut mai sus de pildă); teoremele la care există demonstraţii ``scurte'' pot fi asimilate cu problemele din mulţimea NP (la fiecare pas dintr-o demonstraţie putem aplica mai multe metode de inferenţă, în mod nedeterminist; un algoritm trebuie să ghicească înşiruirea de metode aplicate pentru demonstrarea enunţului); dacă orice problemă din NP este şi în P, atunci putem automatiza o mare parte din demonstrarea de teoreme în mod eficient!

Problema P=NP este foarte importantă pentru criptografie: decriptarea este o problemă din NP (cel care ştie cheia ştie un algoritm determinist polinomial de decriptare, dar cel care nu o ştie are în faţa o problemă pe care nedeterminist o poate rezolva în timp polinomial). Dacă s-ar demonstra că P=NP acest lucru ar avea consecinţe extrem de importante, iar CIA si KGB ar fi într-o situaţie destul de proastă, pentru că toate schemele lor de criptare ar putea fi sparte în timp polinomial (asta nu înseamnă neapărat foarte repede, dar oricum, mult mai repede decît timp exponenţial)!

Mai mult, în 1971 Cook a demonstrat că există o problemă specială în NP (adică pentru care se poate da un algoritm eficient nedeterminist), numită problema satisfiabilităţii (notată cu SAT). Problema este foarte simplă: dacă se dă o formulă booleană care cuprinde mai multe variabile, poate fi formula făcută adevărată dînd anumite valori variabilelor? De pildă formula $(x_1 \land x_2) \lor (x_1 \land \lnot x_2)$ devine adevărată pentru x₁=adevărat şi x₂ arbitrar. SAT este foarte importantă, pentru că Cook a demonstrat că dacă SAT poate fi rezolvată în P (adică folosind un algoritm determinist polinomial), atunci orice problemă din NP poate fi rezolvată în timp polinomial! Problema satisfiabilităţii este cumva ``cea mai grea problemă'' din NP, pentru că rezolvarea oricărei alte probleme din NP se poate face ``mai repede'' decît a ei. Din cauza asta SAT se numeşte o problemă NP-completă.

De la Cook încoace s-au mai descoperit cîteva sute de probleme NP-complete. Unele probleme care se ivesc foarte adesea în practică s-au dovedit NP-complete! Acesta este un alt motiv pentru care clasa atît de abstractă NP a problemelor cu algoritmi nedeterminişti este atît de importantă: foarte multe probleme practice au algoritmi polinomiali nedeterminişti, dar cei mai buni algoritmi determinişti iau un timp exponenţial!

Iată cîteva exemple de probleme NP-complete:

Problema comis-voiajorului (turneu Hamiltonian de cost minim): dîndu-se o reţea de oraşe, o reţea de drumuri între oraşe şi o lungime k, există un traseu de cost mai mic decît k trecînd prin fiecare oraş o singură dată şi revenind la punctul de plecare?
Dîndu-se o mulţime de numere naturale, se poate împărţi în două mulţimi de numere de sume egale²?
``Clica'': dîndu-se un graf G şi un număr k, are G un subgraf complet cu k vîrfuri (adică o mulţime de k vîrfuri unite fiecare cu fiecare)?
``Acoperire'': dîndu-se un graf G şi un număr k, pot alege k vîrfuri în aşa fel încît toate muchiile din G au un capăt ales?

O cantitate enormă de efort şi ingeniozitate a fost risipită pentru a încerca să se demonstreze că P=NP sau opusul acestei afirmaţii, dar nici un rezultat concret nu a fost obţinut. Credinţa cvasi-unanimă este că P $\not=$ NP, dar numai matematica poate oferi vreo certitudine...

Din cauză că foarte multe probleme practice sunt în NP, şi ca aparent nu putem avea algoritmi determinişti eficace pentru ele, cercetătorii şi-au îndreptat atenţia asupra unor clase noi de algoritmi, care vor face obiectul secţiunilor următoare.

Algoritmi aproximativi

În secţiunile care urmează folosim tot timpul premiza nedemonstrată că P $\not=$ NP. Dacă P=NP, atunci problemele pe care ne batem capul să le rezolvăm prin metode ciudate pot fi de fapt rezolvate exact şi eficient, aşa că restul articolului cade şi nu se mai ridică.

Optim şi aproximare

Foarte multe probleme de optimizare se dovedesc a fi NP-complete³: probleme în care vrem să calculăm maximumul sau minimumul a ceva. Bine, dar dacă de fapt mă mulţumesc să obţin o valoare care nu este chiar optimă, dar este ``suficient de aproape''? Poate în acest caz complexitatea problemei poate fi redusă, şi sunt în stare să scriu un algoritm eficient... (polinomial). Avem deci de a face cu un compromis:

solutie optima;                         solutie sub-optima:
                      <-------------->
algoritm NP sau                         algoritm polinomial
algoritm exponential

Într-adevăr, această metodă se bucură de un oarecare succes, dar nu de unul general. Algoritmii care rezolvă o problemă de optimizare în speranţa unui rezultat sub-optimal se numesc ``algoritmi aproximativi''.

Există o sumedenie de rezultate în ceea ce priveşte problemele de optimizare şi aproximările lor. Se demonstrează că unele probleme pot fi foarte bine aproximate (putem obţine soluţii cît dorim de aproape de optim în timp polinomial), altele pot fi aproximate numai în anumite limite (de exemplu putem obţine soluţii de 2 ori mai slabe, dar deloc mai bune), sau altele nu pot fi aproximate deloc (în ipoteza că P $\not=$ NP).

Teoria algoritmilor aproximativi este relativ recentă (deşi ideea există de multă vreme), iar unele rezultate sunt extrem de complicate. Ne vom mulţumi să dăm nişte exemple pentru a ilustra algoritmi aproximativi în acţiune, şi tipul de rezultate care se pot obţine.

Vom ilustra două rezultate diferite din teoria algoritmilor aproximativi: algoritmi de aproximare relativă, algoritmi de aproximare absolută a soluţiei (lămurim terminologia imediat).

Să notăm o instanţă a unei probleme cu I. Fie OPT(I) valoarea soluţiei optime pentru acea instanţă (care există, dar pe care nu ştim s-o calculăm eficient), şi fie A(I) valoarea calculată de algoritmul nostru aproximativ. Numim aproximaţia absolută dacă există un număr K, independent de instanţa I, care are proprietatea că |OPT(I) - A(I)| < K. Numim aproximaţia relativă dacă există un R (numit ``performanţă'') astfel ca pentru orice instanţă I avem (A(I) / OPT(I)) < R (dacă problema caută un maximum, atunci fracţia din definiţie trebuie inversată).

Problema rucsacului

Iată o variantă a problemei rucsacului care este NP-completă (nu am discutat deloc în acest articol despre cum se demonstrează aşa ceva, aşa că trebuie să mă credeţi pe cuvînt), dar pentru care se poate obţine cu foarte mare uşurinţă un algoritm aproximativ relativ eficient.

Se dau o mulţime (mare) de rucsaci de capacitate egală (cunoscută, un număr natural). Se mai dă o mulţime finită de obiecte, fiecare de un volum cunoscut (număr natural). Întrebarea este: care este numărul minim de rucsaci necesari pentru a împacheta toate obiectele?

Problema rucsacului are un algoritm de aproximare relativă cu performanţă 2.

Algoritmul este banal: metoda ``greedy'': pune de la stînga fiecare greutate în primul rucsac liber:

Date de intrare: nrobiecte, capacitate, marime[1..nrobiecte]

Initializari:
o, folositi := 1, 0
do o <= nrobiecte -> liber[o] := capacitate od

Algoritm:
o := 1
do o <= nrobiecte -> 
    r := 1
    do (liber[r] < marime[o]) -> r := r+1
    od
    folositi, liber[r], o := 
        max(r, folositi), liber[r] - marime[o], o+1
od

Cum demonstrăm că performanţa relativă este 2? Foarte simplu: să observăm că la sfîrşitul algoritmului nu pot exista doi rucsaci folosiţi pe mai puţin de jumătate amîndoi, pentru că atunci conţinutul celui de-al doilea ar fi fost vărsat în primul. Cu alte cuvinte, la terminare avem: liber[r] < 1/2 capacitate. Dar dacă însumăm pentru toţi rucsacii, vom avea că spaţiul liber este mai puţin de jumătate din cel disponibil, deci cel ocupat este mai mult de jumătate. Dar dacă obiectele au mărime totală M, atunci orice-am face nu putem folosi mai puţin de M spaţiu total pentru a le împacheta. Dar noi am folosit mai puţin de M + M = 2M, deci algoritmul are performanţă 2. QED.

Performanţa absolută; un rezultat negativ

Vom folosi o altă problemă NP-completă, pentru care avem imediat un algoritm de aproximare relativă de performanţă 2, dar pentru care vom demonstra că nu există nici un algoritm de aproximare absolută.

Problema este cea a acoperirii unui graf, enunţată mai sus. Ca problemă de optimizare, ea se enunţă astfel: ``care este numărul minim de vîrfuri care trebuie ``acoperite'' astfel ca toate muchiile dintr-un graf să fie atinse?''

Pentru această problemă algoritmul greedy nu face multe parale ca algoritm de aproximare. Există însă un algoritm relativ simplu, cu performanţă 2, care se foloseşte însă de un alt algoritm clasic, cel al ``cuplării'' (matching). Fără a intra în detalii, există un algoritm polinomial relativ sofisticat pentru a calcula cuplări maximale pe grafuri⁴. Calculăm o cuplare maximală, după care luăm capetele tuturor muchiilor care o formează: astfel obţinem o acoperire (uşor de demonstrat) care e cel mult dublă ca mărime faţă de optim (pentru că în optim trebuie să se găsească cel puţin cîte un vîrf pentru fiecare muchie din cuplare, iar noi am luat cîte două).

Iată şi un rezultat negativ interesant: pentru orice K fixat, nu există nici un algoritm care să dea pentru problema acoperirii o soluţie aproximativă absolută la distanţa K de cea optimă pentru orice instanţă. Demonstraţia este foarte simplă, odată ce ai văzut ideea, şi se bazează pe ``tehnica amplificării''. Iată cum se face, prin reducere la absurd:

Să presupunem că avem un algoritm A care calculează pentru orice graf o acoperire care este cu cel mult K noduri mai mare ca cea optimă (K e fixat). Cu alte cuvinte |OPT(G) - A(G)| < K. Să luăm o instanţă arbitrară a problemei cuplării, G. Formăm un nou graf G₁ din G, care nu este conex, şi care constă din K+1 copii ale lui G, alăturate. Aceasta este o instanţă perfect corectă a problemei acoperirii, aşa că rulăm pe ea algoritmul nostru A. Acesta va oferi o acoperire care are cel mult cu K noduri mai mult decît acoperirea optimă. (Vă reamintesc notaţiile: OPT(G) este valoarea optimă: numărul minim de noduri pentru a acoperi muchiile, iar A(G) este valoarea calculată de algoritmul nostru.

Datorită faptului că cele K+1 copii ale lui G sunt neconectate, optimumul pentru G₁ este reuniunea a K+1 optimumuri pentru G. Din cauza asta avem relaţia OPT(G₁) = (K+1) OPT(G). Fie acum H copia lui G pe care A a marcat cele mai multe vîrfuri; atunci A(G₁) <= (K+1) A(H). Dar din proprietăţile lui A avem: |OPT(G₁) - A(G₁)| < K, sau |(K+1) OPT(H) - (K+1) A(H)| < K, ori |OPT(H) - A(H)| < K/(K+1) < 1. Însă ştim că OPT(H) şi A(H) sunt numere naturale, deci am obţinut OPT(H) = A(H)!

Asta înseamnă că dacă avem un algoritm aproximativ absolut pentru problema acoperirii, putem imediat construi un algoritm exact la fel de rapid. Ori asta ar însemna că P=NP, ceea ce am presupus fals.

Exemplele pe care le-am ales sunt în mod deliberat simple; teoria algoritmilor aproximativi este în plină dezvoltare şi are rezultate foarte spectaculoase şi în general complicate. În orice caz, aplicabilitatea ei este imediată, pentru că multe probleme practice care nu pot aştepta au numai rezolvări aproximative.

Algoritmi Monte Carlo

O tehnică foarte spectaculoasă pentru rezolvarea problemelor este cea a folosiri numerelor aleatoare. Practic algoritmii aleatori sunt identici cu cei obişnuiţi, dar folosesc în plus o nouă instrucţiune, care s-ar putea chema ``dă cu banul''. Această instrucţiune generează un bit arbitrar ca valoare.

În mod paradoxal, incertitudinea ne poate oferi mai multă putere...

La ce se foloseşte aleatorismul? Să ne amintim că în general complexitatea unei probleme este definită luînd în considerare cea mai defavorabilă instanţă. De exemplu, pentru problema comis voiajorului, faptul că această problemă este NP-completă nu înseamnă că nu putem rezolva nici o instanţă a ei, ci că există instanţe pentru care algoritmii cunoscuţi nu au prea multe şanse să termine în curînd.

Acest lucru este adevărat şi pentru alte clase de algoritmi; de pildă algoritmul quicksort are pentru majoritatea vectorilor de intrare o comportare O(n log n). Dacă însă datele de intrare sunt prost distribuite, atunci quicksort poate face n² comparaţii. Pentru n=100 asta înseamnă de 10 ori mai mult! Numărul de instanţe pentru care quicksort este slab este mult mai mic decît numărul de instanţe pentru care merge bine. Ce te faci însă dacă într-un anumit context lui quicksort i se dau numai date rele? (Datele preluate din măsurători reale sunt foarte rar complet uniform distribuite). O soluţie paradoxală constă în a amesteca aleator vectorul înainte de a-l sorta.

Complexitatea medie (average case) a lui quicksort este O(n log n). Complexitatea în cazul cel mai rău (worst case) este O(n²). Dacă datele vin distribuite cu probabilitate mare în zona ``rea'', atunci amestecîndu-le putem transforma instanţe care pică în zona ``worst-case'' în instanţe de tip ``average-case''. Fireşte, asta nu înseamnă ca nu putem avea ghinion, şi ca amestecarea să producă tot o instanţă ``rea'', dar probabilitatea ca acest lucru să se întîmple este foarte mică, pentru că quicksort are puţine instanţe rele⁵.

Acesta este un caz de folosire a aleatorului pentru a îmbunătăţi performanţa medie a unui algoritm.

Cîteodată cîştigul este şi mai mare, pentru că putem rezolva probleme NP-complete foarte rapid folosind aleatorismul. De obicei avem însă un preţ de plătit. Cînd folosim algoritmi din clasa prezentată mai jos, putem risca să nu primim răspunsul corect.

Algoritmi Las Vegas

Evoluţia unui algoritm care foloseşte numere aleatoare nu mai depinde numai de datele de intrare, ci şi de numerele aleatoare pe care le generează. Dacă are ``noroc'' algoritmul poate termina repede şi bine; dacă dă prost cu zarul, ar putea eventual chiar trage o concluzie greşită. (În cazul quicksort de mai sus răspunsul este întotdeauna corect, dar cîteodată vine mai greu. Aceasta este diferenţa dintre algoritmii Monte Carlo, mereu corecţi, şi cei Las Vegas, care pot uneori, rar, greşi.)

Vom defini acum algoritmii probabilişti pentru probleme de decizie (ţineţi minte, la care răspunsul este Da sau Nu). Majoritatea problemelor pot fi exprimate în forma unor probleme de decizie, deci simplificarea nu este prea drastică.

Există două clase de algoritmi probabilişti, dar ne vom concentra atenţia numai asupra uneia dintre ele, pentru care vom da şi două exemple simple şi spectaculoase. Vom defini totodată clasa problemelor care pot fi rezolvate probabilist în timp polinomial, numită RP (Random Polinomial).

Observaţi că dacă indicăm de la început care sunt numerele aleatoare care vor fi generate, evoluţia algoritmului este perfect precizată.

Definiţie: O problemă de decizie este în RP dacă există un algoritm aleator A care rulează într-un timp polinomial în lungimea instanţei (n^c pentru un c oarecare), şi care are următoarele proprietăţi:

Dacă răspunsul la o instanţă I este ``Da'', atunci cu o probabilitate mai mare de 1/2 algoritmul va răspunde ``Da''.
Dacă răspunsul la o instanţă I este ``Nu'', atunci cu probabilitate 1 algoritmul va răspunde ``Nu''.

De cine este dată ``probabilitatea'' de mai sus? De numărul de şiruri aleatoare. Cînd rulăm un algoritm aleator pentru o instanţă I avem la dispoziţie 2^{n^c} şiruri aleatoare de biţi; pentru unele dintre ele algoritmul răspunde ``Da'', pentru celelalte răspunde ``Nu''. Ceea ce facem este să numărăm pentru cîte şiruri algoritmul ar răspunde ``da'' şi să facem raportul cu 2^{n^c}. Aceasta este probabilitatea ca algoritmul să răspundă ``da''. Opusul ei este probabilitatea să răspundă ``nu''.

O tehnică foarte simplă de amplificare poate creşte nedefinit această probabilitate: dacă executăm algoritmul de 2 ori pe aceleaşi date de intrare, probabilitatea de a greşi pentru răspunsuri ``nu'' rămîne 0. Pe de altă parte, ajunge ca algoritmul să răspundă măcar odată ``da'' pentru a şti că răspunsul este ``da'' cu siguranţă! Din cauza asta, dacă probabilitatea de eroare este p pentru algoritm, executînd de k ori probabilitatea coboară la p^k (nu uitaţi ca p este subunitar, ba chiar sub 1/2). Această metodă se numeşte ``boost'' în engleză, şi face dintr-un algoritm probabilist slab ca discriminare o sculă extrem de puternică!

Pentru a scădea probabilitatea de eroare a unui algoritm care poate greşi cu probabilitatea p pînă sub o limită dorită siguranta, se procedează astfel:

raspuns, probabilitate = nu, 1
do (raspuns = nu) and (probabilitate > siguranta) ->
        raspuns, probabilitate := executa(algoritm), probabilitate * p
od

Iată un exemplu şi o aplicaţie al algoritmilor aproximativi.

Rădăcinile unui polinom

Fie un polinom de mai multe variabile, x₁, x₂, ... x_n. Acest polinom poate fi descris printr-o formulă aritmetică, de pildă: (x₁ + 1) (x₂ + 1) ... (x_n + 1). Întrebarea este: este acest polinom identic nul sau nu?

Desigur, o posibilitate este de a ``expanda'' acest polinom în formă canonică (sumă de produse), şi de a compara fiecare coeficient cu 0. Dar în general această operaţie poate lua un timp exponenţial! (De exemplu polinomul anterior generează 2ⁿ termeni!).

Soluţia este să ne bazăm pe două proprietăţi elementare ale polinoamelor:

Un polinom identic nul este 0 pentru orice combinaţie de valori a variabilelor;
Un polinom ne-nul are ``puţine'' rădăcini într-un corp⁶.

De aici rezultă că:

Dacă polinomul este nul, atunci evaluarea lui în orice punct va da 0;
Dacă polinomul este ne-nul, atunci probabilitatea de a obţine valoarea 0 într-un punct (v₁, v₂, ... v_n) ales arbitrar din Sⁿ este < d/|S|.

Pentru polinomul de mai sus gradul este n, şi putem alege pentru K de exemplu Z_p, unde p este un număr prim relativ mare în raport cu n (de două ori mai mare ajunge!).

Alegînd arbitrar numerele v₁, v₂, ..., v_n în Z_p şi evaluînd q(v₁, v₂, ..., v_n) mod p, putem imediat afirma cu probabilitate mare > 1 - n/p despre q dacă este nul sau nu! Observaţi că evaluarea polinomului nu este prea costisitoare, putîndu-se face în timp polinomial în lungimea expresiei care descrie polinomul.

Folosind metoda de ``boost'' putem creşte rapid siguranţa noastră despre rezultatul algoritmului.

Izomorfismul arborilor

Iată şi o aplicaţie imediată a acestei proprietăţi.

Se dau doi arbori, cu rădăcina precizată. Sunt aceşti doi arbori ``izomorfi'' (identici prin re-ordonarea fiilor)? Această problemă este surprinzător de dificilă pentru un algoritm determinist (am impresia chiar că este NP-completă). Iată însă o soluţie aproape imediată: construim pentru fiecare arbore cîte un polinom care nu depinde de ordinea fiilor unui nod, în aşa fel încît dacă şi numai dacă arborii sunt izomorfi polinoamele sunt egale. Apoi pur şi simplu testăm ca mai sus dacă polinomul diferenţă este nul.

O metodă de a asocia recursiv un polinom unui arbore este de pildă următoarea: fiecărui nod îi asociem o variabilă x_k, unde k este înălţimea nodului (distanţa pînă la cea mai depărtată frunză). Frunzele vor avea toate asociate variabila x₀. Apoi asociem nodului v de înălţime k cu fii v₁, ... v_l polinomul f_v = (x_k - f_v₁) (x_k - f_v₂) ... (x_k - f_{v_l}). Se arată uşor că polinoamele sunt egale pentru arbori izomorfi, bazîndu-ne pe unicitatea descompunerii în factori a unui polinom. Gradul polinomului asociat unui nod este egal cu suma gradelor fiilor, care la rîndul ei este egală cu numărul de frunze care se află sub acel nod (cum se demonstrează imediat prin inducţie după înălţime). Şi asta-i tot!

Pentru a încheia secţiunea, să observăm că singurul algoritm eficient cunoscut pentru a verifica primalitatea unui număr este tot probabilist⁷! Pentru că numerele prime mari stau la baza criptografiei cu cheie publică în sistemul RSA (probabil cel mai răspîndit la ora actuală), iată că unele dintre cele mai importante aplicaţii se bazează indirect pe algoritmi probabilişti. Nimeni nu va putea obiecta asupra utilităţii lor!

Algoritmi on-line

Adesea trebuie luate decizii cu informaţii incomplete. Un caz particular este luarea de decizii pe măsură ce datele devin disponibile. Deciziile afectează viitorul, dar sunt luate fără a avea cunoştinţe despre datele viitoare. Sa vedem în acţiune un exemplu foarte simplu:

Problema schiorului

Se pune problema: ce este mai bine: să închiriezi sau să cumperi schiuri? (Vom presupune că preţul schiurilor este constant de-a lungul timpului, ca să simplificăm problema). Dilema constă din faptul că în fiecare sezon, nu ştii dacă te vei mai duce odată. Dacă le cumperi şi nu te mai duci, ai dat banii degeaba. Dacă le tot închiriezi şi te duci des, s-ar putea să le plăteşti de mai multe ori. Totuşi, trebuie să iei o decizie. Pe care?

Există un răspuns foarte simplu, care promite nu că dă rezultatul cel mai ieftin în orice circumstanţă, ci doar că nu vei cheltui de două ori mai mult decît în cazul în care ai face decizia perfectă (decizia perfectă este cea care ştie precis dacă te vei mai duce, şi de cîte ori; ea nu este accesibilă decît ``post-factum'', deci este pur teoretică).

Algoritmul este: închiriezi schiuri pînă ai dat pe chirie costul schiurilor. După aceea dacă mai vrei să mergi le cumperi. Voi demonstra rapid că în felul ăsta orice s-ar întîmpla nu pierzi mai mult de jumate din banii pe care i-ai fi cheltuit în cazul ideal.

Avem 3 posibilităţi:

Te opreşti înainte de a le cumpăra: în cazul ăsta ai jucat perfect, pentru că ai schiat şi nu puteai ieşi mai ieftin nicicum;
Te opreşti imediat după ce le-ai cumpărat. În cazul ăsta ai dat de două ori preţul (odată pe închirieri, şi odată pe cumpărare), dar ai schiat cît ai fi putut schia dînd numai odată preţul (mai ieftin de odată nu puteai ieşi);
Te opreşti mai tîrziu: în cazul ăsta cel mai ieftin era tot să le cumperi din prima zi, deci iar ai cheltuit dublu.

Orice altă schemă foloseşti pentru a decide cumpărarea, există un scenariu în care poţi cheltui mai mult de dublu faţă de optim.

Algoritmii on-line apar foarte natural într-o mulţime de situaţii: de exemplu în reţele de calculatoare, algoritmii care decid traseul unui pachet cu informaţii sunt algoritmi on-line; dacă decid trasee proaste, reţeaua poate deveni supra-aglomerată în viitor; astfel de algoritmi nu au idee despre cererile viitoare, aşa că acţionează cu informaţie incompletă.

Un alt exemplu este în sistemele de operare: algoritmii după care cache-urile (sau sistemele de memorie virtuală) aleg paginile care trebuie înlocuite. Alegerea aceasta nu poate fi optimă în absenţa informaţiilor despre viitoarele cereri. Cu toate acestea, anumite alegeri sunt mai bune decît altele.

Un al treilea exemplu, tot din contextul sistemelor de operare, este al algoritmilor de planificare, care trebuie să stabilească în ce moment se execută fiecare proces pe un calculator (paralel). Acolo unde minutul de rulare costă o grămadă de bani, deciziile trebuie să risipească cît mai puţin timp. Însă job-uri pentru prelucrare sosesc dinamic, aşa că algoritmii trebuie să facă faţă unui mediu în continuă schimbare.

Algoritmii on-line sunt în general analizaţi comparîndu-i cu algoritmii off-line, care ar avea înainte de a face deciziile informaţii perfecte despre toate cererile viitoare. Este clar că informaţia aceasta este un mare avantaj, aşa că în general algoritmii on-line au performanţe mult mai proaste decît cei corespunzători off-line.

Cercetările în acest domeniu sunt doar la început; se explorează şi variante de algoritmi hibrizi on/off-line, în care algoritmul are o idee despre viitor, dar nu neapărat o vedere completă. Asta nu face întotdeauna sarcina algoritmului mai simplă, pentru că adesea problema cu informaţie completă este NP-completă...

Rezumat

În acest articol am trecut razant printr-o grămadă de probleme fascinante. Iată recapitulate sumar conceptele esenţiale întîlnite:

Orice algoritm se exprimă folosind un set de operaţiuni elementare;
Un algoritm poate rezolva o instanţă a unei probleme dintr-o clasă întreagă;
Complexitatea algoritmilor este o funcţie de mărimea instanţei şi măsoară operaţiile efectuate pentru a rezolva cel mai nefavorabil caz;
Complexitatea se exprimă concis prin ordinul de mărime al funcţiei complexitate spre infinit;
Invarianţii sunt o metodă foarte utilă pentru a demonstra corectitudinea unui algoritm;
Complexitatea unei probleme este complexitatea celui mai rapid algoritm care o poate rezolva;
Există probleme care au nevoie de un timp exponenţial (în mărimea problemei) sau chiar mai mult pentru a fi rezolvate; există probleme care nu se pot rezolva deloc cu algoritmi;
Clasa problemelor care au algoritmi nedeterminişti polinomiali include foarte multe probleme practice; nimeni nu ştie cum să rezolve aceste probleme în mod eficient;
Clasa problemelor NP-complete este un set de probleme care se rezolvă toate la fel de repede; un algoritm care ar rezolva deterministic polinomial una din ele ar cauza rezolvarea tuturor problemelor din NP rapid;
Algoritmii aproximativi încearcă să găsească mai repede soluţii sub-optimale la probleme grele;
Algoritmii aleatori folosesc aleatorismul pentru a forţa comportarea unor probleme mai curînd ca în cazul mediu decît ca în cazul cel mai rău;
Algoritmii probabilişti găsesc soluţiile cu mare probabilitate, dar nu întotdeauna, însă o fac repede;
Algoritmii on-line trebuie să ia decizii înainte de a avea toate informaţiile disponibile;
Multe domenii practice beneficiază masiv de noile tehnici, cea mai notabilă fiind criptografia.

Footnotes

... $\Omega$ ¹: Mai exact $f \in \Omega(g) \Leftrightarrow f \in O(g) \land g \in O(f)$ .
... egale ²: Problema este într-adevăr NP-completă, dacă socotim ca mărime de intrare lungimea tuturor numerelor în biţi; altfel există un algoritm de programare dinamică de complexitate S n, unde S este suma numerelor, iar n este numărul de numere. Observaţi însă că S este exponenţială în lungimea numerelor.
... NP-complete ³: Cititorul atent va observa că noţiunea de NP-completitudine a fost definită numai pentru probleme de decizie: cu răspuns Da/Nu, pe cînd problemele de optimizare au în general un răspuns numeric; cititorul poate însă să fie liniştit, pentru că putem re-formula o problemă de optimizare ca o problemă de decizie: în loc de ``care este drumul minim?'', întrebăm ``nu-i aşa că există un drum mai scurt de 100?''.
... grafuri ⁴: O cuplare este un set de muchii care nu are vîrfuri comune, iar o cuplare maximală este una care are un număr maxim de muchii.
... rele ⁵: Numărul de instanţe rele poate fi estimat din distribuţia variabilei aleatoare complexitate, şi este într-adevăr mic.
... corp ⁶: Aceasta este Teorema Lipton-Schwartz-Zippel: fie $S \subseteq K$ o submulţime a unui corp K, iar $q(\overline{x})$ un polinom de n variabile de grad d cu coeficienţi în K. Atunci ecuaţia $q(\overline{x}) = 0$ are cel mult d |S|^n-1 soluţii în S.
... probabilist ⁷: Aşa se generează numere prime: se generează un număr aleator şi se verifică primalitatea cu un astfel de algoritm.