Teoria complexităţii

Dintre ramurile informaticii, teoria complexităţii a fost întotdeauna pentru mine cea mai fascinantă, pentru că pune cele mai cutezătoare întrebări şi dă cele mai cuprinzătoare răspunsuri. La un moment dat intenţionam să îmi dedic chiar activitatea de cercetare acestui domeniu, dar paşii mei s-au păstrat pe o cărare mult mai practică. Am încercat însă să fiu un amator informat în ceea ce priveşte acest fascinant domeniu. Articolul de faţă va încerca să vă transmită cîteva dintre motivele fascinaţiei mele.

Pentru că subiectul acesta este foarte generos, mă văd din nou obligat în a face un articol cu mai multe episoade; îmi cer scuze cititorilor care nu vor cumpăra toate numerele revistei.

Am mai publicat în PC Report despre subiecte înrudite: un articol amplu în 1997 discuta despre direcţii noi de cercetare în algoritmi, iar cele două numere din PC Report anterioare celui de faţă au fost consacrate celei mai importante probleme nerezolvate din teoria complexităţii, problema satisfiabilităţii. Cititorii interesaţi pot găsi aceste texte în pagina mea de web.

Din păcate îndeletnicirea mea este oarecum ingrată: în primul rînd este dificil să vorbeşti despre ceva la care nu te pricepi cu adevărat; în al doilea rînd, substanţa însăşi a acestui domeniu este foarte formală; nu i se poate da dreptate fără a folosi o doză substanţială de matematică, ori acest gen de literatură nu este de loc pe potriva revistei PC Report.

Ca atare voi recurge la o practică reprobabilă: voi încerca să vă povestesc despre rezultatele cele mai remarcabile obţinute în acest domeniu, dar fără a oferi întotdeauna demonstraţii matematice, şi adesea chiar fără a exprima foarte precis noţiunile despre care vorbesc. Voi consuma cu neruşinare ``crema'' acestui domeniu, vînturînd în faţa ochilor dumneavoastră cele mai spectaculoase rezultate, dar fără a vă arăta toată sudoarea care stă în spatele lor. Dacă asta vă va trezi curiozitatea în a aprofunda domeniul, sau dacă doar veţi privi cu mai mult respect domeniul informaticii, nu ca pe o simplă meşteşugăreală, dar ca pe o ştiinţă în toată regula, mă voi putea declara satisfăcut.

Cititorul cu înclinaţii matematice poate însă să fie liniştit: toate lucrurile despre care pomenesc sunt de fapt foarte precis formalizate, şi suportate de demonstraţii în toată legea. În plus, matematica folosită în teoria complexităţii este relativ simplă: toate aceste lucruri ar trebui să fie accesibile unui elev de liceu care-şi dă (ceva mai multă) osteneală; cu certitudine, matematica studiată în facultate este mult mai complicată decît cea întîlnită în studiul teoriei complexităţii.

În mod interesant, asta nu înseamnă că teoria complexităţii este mai uşoară; dimpotrivă, minţi briliante au cucerit cu multă trudă rezultatele acesteia. Ceea ce e adevărat este că matematica folosită în teoria complexităţii are mult mai puţină structură, şi că obiectele manipulate sunt mult mai simple. Cel mai adesea avem de-a face cu obiecte finite, şi aproape întotdeauna cu obiecte numărabile, discrete. Obiectul fundamental este şirul de caractere formate din litere ale unui alfabet finit: o structură mult mai simplă decît cele întîlnite de pildă în analiza matematică.

Desigur, faptul că o problemă are un enunţ simplu nu înseamnă de loc că are şi o soluţie simplă; cea mai puternică mărturie este probabil Marea teoremă a lui Fermat, al cărei enunţ poate fi explicat şi unui şcolar, dar a cărei rezolvare a cerut trei sute de ani de eforturi încordate. De fapt, vom vedea că în teoria complexităţii există o sumă de probleme fundamentale nerezolvate; putem chiar spune că majoritatea problemelor fundamentale sunt încă nerezolvate.

Dar informatica este o ştiinţă exactă extrem de tînără; mult mai tînără decît matematica sau fizica. Sunt convins că cele mai interesante rezultate vor apărea abia în viitor; ceea ce ne minunează în ziua de astăzi este echivalentul uimirii pitagorenilor în faţa triunghiului dreptunghic: doar umbra unei colosale frumuseţi matematice.

Teoria complexităţii: o ştiinţă despre limitele inferioare

Teoria complexităţii (complexity theory) se ocupă cu studiul lucrurilor care se pot calcula atunci cînd resursele pe care le avem la dispoziţie sunt limitate. Resursele fundamentale în teoria tradiţională erau:

dar dezvoltările mai recente au arătat că alte genuri de resurse au un impact foarte important asupra lucrurilor care se pot calcula, cum ar fi:

Dintr-un anumit punct de vedere, teoria complexităţii este exact opusul teoriei algoritmilor, care probabil partea cea mai dezvoltată a informaticii teoretice: dacă teoria algoritmilor ia o problemă şi oferă o soluţie a problemei în limitele unor resurse, teoria complexităţii încearcă să arate cînd resursele sunt insuficiente pentru a rezolva o anumită problemă. Teoria complexităţii oferă astfel demonstraţii că anumite lucruri nu pot fi făcute, pe cînd teoria algoritmilor arată cum lucrurile pot fi făcute.

De exemplu, atunci cînd învăţăm un algoritm de sortare ca quicksort, demonstrăm că problema sortării a n numere se poate rezolva în timp proporţional cu n log n. Ştim deci că sortarea se poate face în timp cel mult n log n, sau mai puţin.

Pe de altă parte, teoria complexităţii ne arată că pentru a sorta n numere oarecare ne trebuie cel puţin timp n log n, şi că este imposibil să sortăm mai repede, dacă nu avem informaţii suplimentare despre valorile de sortat.

Combinînd aceste două rezultate, deducem că problema sortării are complexitatea exact n log n, pentru că:

Această stare de fapt este una extrem de fericită, şi din păcate foarte rară: pentru majoritatea problemelor pe care le cunoaştem, există o distanţă mare între cea mai bună posibilitate de rezolvare pe care o cunoaştem şi limita inferioară cea mai ridicată pe care o putem demonstra. Situaţia este ca în figura 1.

**Figura 1:** Existenţa unui algoritm pentru a rezolva o problemă oferă o limită superioară pentru complexitatea problemei: în regiunea albastră, din dreapta, putem rezolva problema. Teoria complexităţii găseşte limite inferioare: dacă ne plasăm în regiunea roşie, cu certitudine problema este insolvabilă. Foarte adesea, între cele două regiuni există o zonă (haşurată cu negru) despre care nu putem spune nimic. Din păcate, această zonă este adesea foarte mare ca întindere.
$\begin{figure}\centerline{\epsfxsize=12cm\epsffile{limite.eps}}\end{figure}$

Chiar pentru probleme aparent banale, complexitatea minimă este adesea necunoscută. De exemplu, algoritmul cel mai bun cunoscut pentru a înmulţi două numere de n cifre are complexitatea n log log n, dar limita inferioară oferită de teoria complexităţii este de n. Algoritmul învăţat în şcoala primară pentru înmulţire are complexitatea n². Nimeni nu ştie cît de jos poate fi împinsă această limită, dar teoria complexităţii ne garantează ca nu mai jos de n (de fapt în cazul de faţă nu e nevoie de nici o teorie pentru a ne spune asta: în timp mai puţin de n nu poţi nici măcar să citeşti toate cifrele numerelor de înmulţit).

Pentru foarte multe probleme importante, distanţa între limitele inferioară şi superioară cunoscute este enormă: de exemplu pentru problema satisfiabilităţii, căreia i-am consacrat ultimele mele două articole, limita superioară este o funcţie exponenţială (2ⁿ) iar cea inferioară este una polinomială (n^k), pentru un k constant, independent de problemă.

Într-un anume sens, teoria complexităţii are o sarcină mult mai grea decît cea a algoritmilor: teoria algoritmilor demonstrează propoziţii de genul: ``există un algoritm de complexitate n log n care înmulţeşte două numere''. Acest lucru este de obicei făcut chiar construind acel algoritm. Pe de altă parte, teoria complexităţii trebuie să demonstreze teoreme de genul ``Nu există nici un algoritm care rezolvă această problemă în mai puţin de n log n paşi''. Ori aşa ceva este nu se poate demonstra în mod direct: există un număr infinit de algoritmi, deci nu putem pur şi simplu să-i verificăm pe toţi.

Modele de calcul şi resurse

Am tot menţionat tot felul de limite (ex. n²), dar nu am spus ce înseamnă acestea. Atît teoria complexităţii, cît şi teoria algoritmilor, măsoară complexitatea în acelaşi fel, şi anume asimptotic. Asta înseamnă că măsurăm numărul de operaţii făcute ca o funcţie de cantitatea de date care ne este oferită spre prelucrare, şi că împingem această cantitate spre infinit. Atunci complexitatea este exprimată ca o funcţie pe mulţimea numerelor naturale: pentru fiecare mărime de intrare, avem o complexitate. Dacă putem avea mai multe date de intrare cu aceeaşi mărime (de exemplu, cînd sortăm putem avea mai mulţi vectori de lungime n), atunci complexitatea pentru intrarea n este luată ca fiind maximumul dintre toate valorile: max_(|i|=n) f(i), unde f este complexitatea şi i sunt datele de intrare (simbolul | | reprezintă mărimea datelor).

Calculatoarele: procesoare de limbaje

Cum măsurăm datele de intrare şi cum măsurăm resursele? Întrebarea este perfect legitimă, şi merită o clarificare.

În primul rînd, toate datele pe care le vom prelucra sunt exprimate folosind literele unui alfabet. Nu contează prea tare care este alfabetul, atîta vreme cît are cel puţin două semne diferite.

Dacă fixăm un alfabet, putem vorbi de şiruri de caractere (strings) din acel alfabet. Putem de asemenea vorbi de limbaje: un limbaj este o mulţime de şiruri. Definiţia aceasta pare foarte simplă, dar este foarte utilă: de aici înainte putem enunţa absolut toate procesările făcute de un calculator în termeni de operaţii pe limbaje.

De exemplu, putem considera limbajul format din mulţimea şirurilor care încep cu semnul + sau -, urmate de un şir de cifre, urmate eventual de o virgulă, de alte cifre, şi eventual nişte cifre între paranteze. Acest limbaj poate descrie numerele raţionale, inclusiv pe cele periodice, în notaţia pe care am învăţat-o în şcoala primară; de exemplu -312,413(3) este un şir din această mulţime. Putem de asemenea caracteriza alte limbaje foarte interesante, ca: limbajul tuturor expresiilor aritmetice corecte, limbajul Pascal, format din toate şirurile de caractere care sunt programe Pascal corecte, etc.

Un calculator va primi deci la intrare un şir finit de caractere, şi va produce la ieşire un altul. Putem măsura foarte precis lungimea unui şir de caractere prin numărul de caractere care-l compun. Aceasta este definiţia ``mărimii'' datelor de intrare.

Un algoritm se va aştepta ca datele de intrare să fie dintr-un anumit limbaj; în acest caz, el va transforma fiecare cuvînt de la intrare într-un cuvînt dintr-un alt limbaj. De pildă, un algoritm care sortează un şir de numere se aşteaptă ca la intrare datele să fie un şir de numere separate de spaţii; pentru fiecare astfel de şir de numere, el va produce la ieşire un alt şir de numere. Limbajul datelor de intrare este format din şirurile de numere separate de spaţii, limbajul de la ieşire este acelaşi, dar toate numerele dintr-un şir la ieşire vor fi sortate. Ce face algoritmul dacă datele de intrare nu sunt un şir de numere, ci nişte gunoaie? Putem spune că nu ne interesează comportarea algoritmului în astfel de cazuri.

Vedeţi, aparent desfacem firul în patru: cine are nevoie de nişte definiţii atît de amănunţite, încît sunt aproape lipsite de sens? Matematicienii au nevoie: după ce am clarificat exact noţiunile cu care operăm, avem foarte multă libertate în a le manipula în mod precis.

Operaţii cu limbaje

Adesea vom specifica limbajele pornind de la limbaje mai simple, cu ajutorul unor operaţii. De exemplu, putem construi limbaje intersectînd două limbaje, sau luînd reuniunea lor: doar avem de-a face cu mulţimi de cuvinte. De exemplu, dacă intersectăm limbajul tuturor cuvintelor din limba româna -- să-l notăm cu R, un limbaj format din toate cuvintele din DEX şi derivatele lor -- cu limba latină vom obţine un nou limbaj, care constă din toate cuvintele moştenite din latină.

Alte operaţii pe care le putem face sunt: complementarea unui limbaj (complementul unui limbaj L este cel format din toate cuvintele care nu sunt în L) sau concatenarea a două limbaje (L1 concatenat cu L2 este un limbaj format din cuvinte pentru care prima parte e un cuvînt din L1 iar a doua din L2). De exemplu, limbajul propoziţiilor româneşti de două cuvinte este un subset al limbajului R concatenat cu el însuşi.

Decidabilitate

Un loc aparte în studiul complexităţii îl au maşinile care dau totdeauna un răspuns ``da'' sau ``nu''. Cu alte cuvinte, limbajul de ieşire are doar două elemente. Spunem despre astfel de maşini că decid un limbaj: limbajul decis este format din cuvintele de la intrare pentru care maşina răspunde ``da''. Toate problemele pentru care aşteptăm un răspuns ``da'' sau ``nu'' se numesc ca atare probleme de decizie; problema SAT, a satifiabilităţii, căreia i-am dedicat două numere în PC Report, este un exemplu de problemă de decizie.

Problemele de decizie sunt o subclasă foarte interesantă a tuturor problemelor, pentru că adesea putem enunţa orice problemă ca o colecţie de probleme de decizie. Această noţiune a fost prezentată în căzut problemei SAT ca ``autoreducere''. Ideea este însă destul de simplă.

De exemplu, să considerăm problema ``care sunt factorii primi ai numărului n?''. Putem reduce această problemă la mai multe probleme de decizie, care ne dau exact aceeaşi informaţie: ``este 2 un factor prim al lui n'', ``este 3 ...'', etc. Dacă ştim răspunsurile la toate aceste probleme de decizie, putem obţine răspunsul şi la problema iniţială.

Maşina Turing

Am clarificat cum arată datele; cum măsurăm însă resursele consumate? Consumate de fapt de cine?

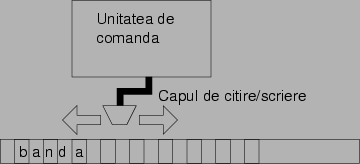
Aveţi perfectă dreptate: ne trebuie un model precis de calcul. Cel mai folosit este un model propus în anii treizeci de marele matematician englez Alan Turing: maşina Turing. Maşina Turing este un calculator redus la esenţe, abstractizat. Maşina Turing (figura 2) este compusă din următoarele piese:

**Figura 2:** Maşina Turing este un model de calcul abstract propus de matematicianul Alan Turing. Ea constă dintr-o bandă infinită, pe care pot fi scrise simboluri, un cap de scriere-citire, care poate fi plimbat pe suprafaţa benzii, şi o unitate de control, care cuprinde un număr finit de reguli care indică maşinii ce să facă la fiecare mişcare în funcţie de litera curentă de pe bandă şi starea în care maşina se află. În pofida simplităţii ei, maşina Turing poate calcula orice poate fi calculat cu cele mai performante supercomputere.
$\begin{figure}\centerline{\epsfxsize=8cm\epsffile{turing.eps}}\end{figure}$

Şi asta-i tot! Un algoritm de calcul este descris de o astfel de maşină, prin toate stările posibile, şi toate aceste reguli, numite reguli de tranziţie, care indică cum se trece de la o stare la alta.

``Ce e prostia asta?'' aţi putea exclama, ``ce poţi face cu maşina asta handicapată?'' Ei bine, poţi face...totul. Alegeţi limbajul dumneavoastră favorit, să zicem C; ei bine, se poate descrie o maşină Turing care să interpreteze (adică să execute) orice program C care i s-ar da scris pe bandă. Putem mima intrarea şi ieşirea unui calculator cerînd ca datele de intrare să fie scrise de la început pe bandă, iar ca datele de ieşire să apară pe bandă cînd maşina termină de calculat¹.

Orice alte modele de calcul care au fost propuse de-a lungul timpului, au fost dovedite a fi mai puţin expresive, sau tot atît de expresive cît maşina Turing. Nimeni nu a fost în stare, pînă acum, să zică: ``eu cred că de fapt maşina Turing e prea limitată; iată care zic eu că sunt operaţiile elementare pe care le avem la dispoziţie, din care ar trebui să exprimăm orice algoritm'', şi să ofere ceva care să fie construibil, şi care să poată face lucruri pe care maşina Turing nu le poate face.

Din cauza asta logicianul Alonzo Church a emis ipoteza că maşina Turing este modelul cel mai general de calcul care poate fi propus; acest enunţ, care nu este demonstrabil în sens matematic, se numeşte ``Teza lui Church''. Acesta este un postulat asupra căruia trebuie să cădem de acord înainte de a putea conversa orice lucru privitor la teoria complexităţii.

Dacă avem un model de calcul, putem defini foarte precis ce înţelegem prin complexitate:

Clase de complexitate robuste

Cînd spun că maşina Turing este la fel de puternică ca orice alt model de calcul, nu înseamnă că poate calcula la fel de repede ca orice alt model de calcul, ci că poate calcula aceleaşi lucruri.

Putem să ne imaginăm tot felul de modificări minore ale maşinii Turing, care o vor face să poată rezolva anumite probleme mai repede. De exemplu, putem să ne imaginăm că maşina are dreptul să mute capul la orice căsuţă dintr-o singură mişcare, fără să aibă nevoie să meargă pas-cu-pas; atunci banda s-ar comporta mai asemănător cu o memorie RAM obişnuită.

Atunci cum de putem discuta despre complexitate, dacă timpul de rezolvare depinde de modelul de execuţie?

Aici teoria complexităţii se desparte de teoria algoritmilor; teoria algoritmilor foloseşte de regulă modelul RAM pentru a evalua complexitatea unui algoritm. Teoria complexităţii face nişte diviziuni mai grosolane.

Şi anume, există nişte clase de complexitate care sunt complet invariante la variatele definiţii ale maşinii Turing: că are două capete de acces la bandă, că poate sări oriunde, complexitatea rămîne aceeaşi. O astfel de clasă de complexitate este clasa tuturor problemelor care se pot rezolva în timp polinomial, o alta este cea a tuturor problemelor care se pot rezolva în spaţiu polinomial, etc. Aceste clase de complexitate sunt numite ``robuste'', pentru că definiţia lor nu depinde de modelul de maşină. Acest lucru se poate demonstra arătînd că o maşină de un anumit model poate simula pe cele diferite fără a cheltui prea multe resurse suplimentare.

Teoria complexităţii mai decretează şi că toate problemele care se pot rezolva în timp polinomial sunt rezolvabile, iar toate cele care au nevoie de mai mult timp sunt intractabile. Această definiţie este în general adevărată din punct de vedere practic, dar trebuie luată cu un grăunte de sare: cîteodată un algoritm n³ este inacceptabil, dacă problema este prea mare, altădată unul de timp chiar exponenţial este tolerabil, dacă maşina cu care-l rulăm este foarte rapidă. Din punct de vedere teoretic, separaţia însă este perfect acceptabilă, pentru că întotdeauna ne gîndim la probleme pentru care mărimea datelor de intrare tinde spre infinit.

Aş vrea să mai fac o observaţie foarte importantă: o problemă este foarte strîns legată de limbajul în care o exprimăm. Iată un exemplu: să considerăm problema înmulţirii a două numere. Dacă limbajul în care lucrăm exprimă numerele în baza 2 (sau orice altă bază mai mare de 2), atunci se cunosc algoritmi de complexitate n log n pentru a face înmulţirea. Pe de altă parte, dacă insistăm să scriem numerele în baza 1 (adică numărul 5 este reprezentat de cinci ``beţişoare'', ca la clasa I), atunci, în mod evident, complexitatea înmulţirii a două numere de lungime totală n este n²: chiar rezultatul înmulţirii lui n cu n este scris cu n² beţişoare, deci nu are cum să ne ia mai puţin timp, pentru că trebuie să scriem rezultatul!

Şi mai spectaculoasă este diferenţa pentru algoritmul care verifică dacă un număr este prim: dacă limbajul de intrare exprimă numerele în baza 2, cel mai bun algoritm cunoscut are complexitatea 2ⁿ, exponenţială, dar dacă scriem numerele în baza 1, complexitatea este n². Acest lucru se întîmplă pentru că un număr scris în baza 1 este mult mai lung decît scris în baza 2 n este scris în baza 2 cu log n cifre).

Deci, cînd enunţaţi o problemă pentru rezolvare cu calculatorul, trebuie să specificaţi şi limbajul în care problema este descrisă; abia apoi puteţi discuta despre complexitatea rezolvării.

Simulări; maşina Turing universală

Oare cum au reuşit matematicienii să demonstreze că maşina Turing este atît de puternică încît este echivalentă cu orice alt model propus de calcul? De pildă, un model extrem de faimos, care este folosit încă foarte ades în teoria limbajelor de programare, este modelul lambda-calculului. Acest model manipulează nişte formule simple conform unor reguli de re-scriere.

Ce sens are să spunem că maşina Turing este la fel de puternică precum lambda-calculul?

Răspunsul stă în simulare: putem arăta că, orice am face cu lambda-calculul, putem efectua şi cu o maşină Turing. Există deci o corespondenţă între fiecare transformare efectuată de regulile lambda-calculului şi un set de transformări pe care maşina Turing le poate face cu simbolurile de pe bandă.

De fapt maşina Turing este atît de puternică încît putem construi o maşină Turing care să simuleze orice altă maşina Turing posibilă.

Pentru a înţelege cum este posibil aşa ceva, trebuie să realizăm două lucruri:

Dacă vă gîndiţi puţin veţi realiza că de fapt aceste lucruri nici măcar nu sunt prea surprinzătoare: de fapt un interpretor de BASIC face acelaşi lucru: primeşte descrierea unei maşini (programul BASIC) şi apoi simulează execuţia acestei maşini pe nişte date de intrare.

calculabilitate

Teorema găurii; diagonalizarea

O întrebare pe care un matematician şi-o pune imediat este: are vreo importanţă cîte resurse dăm unei maşini Turing? Nu cumva totul se poate calcula cu aceeaşi cantitate de resurse?

Există nişte teoreme deosebit de interesante din acest punct de vedere. O teoremă arată că dacă dăm unei maşini mai mult timp (sau spaţiu), atunci ea poate efectua lucruri pe care nici una din maşinile care au mai puţin timp nu le poate efectua. Această teoremă se numeşte ``teorema găurii'' (gap theorem), pentru că arată că între feluritele clase de complexitate există diferenţe: clasa limbajelor care se pot decide în timp n³ este diferită de clasa limbajelor care se pot decide în timp n⁴.

Enunţul teoremei este de fapt destul de încîlcit, şi se bazează pe nişte detalii tehnice, pe care o să le trec sub tăcere. Demonstraţia este însă relativ simplă, şi se bazează pe o tehnică ades folosită în teoria complexităţii, numită diagonalizare. Această tehnică a fost folosită în demonstraţia lui Cantor, pentru a arăta că numerele reale nu sunt numărabile.

Ideea de bază este următoarea: maşina cu mai multe resurse îşi poate permite să facă orice face maşina cu mai puţine resurse, iar după aceea să mai şi prelucreze rezultatul. Cu alte cuvinte, putem construi o maşină cu resurse mai multe, care dă un rezultat diferit de orice maşină mai simplă. Rezultă ca maşina cu mai multe resurse calculează o funcţie diferită de toate celelalte!

Numărabilitate

Teorema găurii se bazează în mod explicit pe faptul că nu există prea multe maşini Turing! Din moment ce fiecare maşină Turing poate fi descrisă printr-un şir de caractere finit, înseamnă că putem enumera toate maşinile Turing. Există astfel un număr numărabil de maşini Turing (deci cu mult mai puţine decît există numere reale!).

O consecinţă interesantă a acestui fapt este că calculatoarele nu pot manipula numerele reale. Există mai multe numere reale decît algoritmi posibili! Limbajele care operează cu numere reale, de fapt manipulează nişte aproximări cu cîteva zeci sau zecimale ale acestora. Nu putem face mai bine de atît nici dacă operăm cu reprezentări simbolice ale numerelor reale (vom putea manipula unele numere reale, dar nu pe toate; vor exista întotdeauna operaţii cu numere reale care nu sunt calculabile).

Există şi alte consecinţe interesante ale acestui fapt. De exemplu, pute privi maşinile Turing ca pe nişte aparate care calculează funcţii de la numerele naturale (N) la N. Ei bine, există $2^{\vert\mbox{\bf N}\vert}$ astfel de funcţii, adică puterea continuului (adică tot atîtea cît numere reale). Dar maşinile Turing sunt doar în număr de $\vert\mbox{\bf N}\vert$ , deci mult mai puţine. Asta înseamnă că există o sumedenie de funcţii N $\rightarrow$ N care nu se pot calcula cu calculatoarele!

Ce dacă, veţi spune, poate toate funcţiile care ne interesează în practică se pot de fapt calcula. Vom vedea de fapt că există funcţii extrem de importante care nu sunt calculabile, oricît de multe resurse am pune la bătaie!

Problema opririi (the halting problem)

Ramura extremă a teoriei complexităţii, care se ocupă cu lucrurile care nu se pot calcula, nici dacă avem o cantitate nelimitată de resurse, se numeşte teoria calculabilităţii.

Teoria calculabilităţii are o sumedenie de rezultate foarte interesante, şi implicaţii foarte mari pentru teoria compilatoarelor (dar nu numai).

Am văzut că putem descrie orice maşină Turing folosind un şir de caractere; putem apoi face prelucrări asupra acestui şir de caractere, pentru a calcula tot felul de proprietăţi ale maşinii Turing codificate astfel. De fapt exact asta face şi un compilator: primeşte un program într-un limbaj (adică descrierea unei maşini Turing), şi generează un alt program ``optimizat'', care face acelaşi lucru, dar mai eficient.

Asta e foarte frumos: putem folosi chiar maşinile Turing pentru a transforma şi calcula lucruri despre maşini Turing. Din păcate optimismul nostru trebuie temperat: sunt foarte multe lucruri pe care nu le putem calcula.

De pildă ne putem pune, poate cea mai naturală, întrebare: dacă bag anumite date de intrare într-o maşina Turing, după cît timp îmi dă rezultatul? Îmi dă rezultatul vreodată, sau intră într-o buclă infinită?

La această întrebare putem răspunde enunţînd cea mai faimoasă teoremă din teoria calculabilităţii, ``teorema opririi'': nu există o maşină Turing, care primind la intrare descrierea unei alte maşini Turing T şi un şir de date de intrare x, să poată spune dacă T se opreşte vreodată cînd primeşte pe x la intrare. Figura 3 ilustrează problema opririi.

**Figura 3:** Problema opririi: o ipotetică maşină care ar putea rezolva problema opririi ar primi descrierile altei maşini pe bandă sîa intrărilor lor, şi ar oferi un răspuns ``da'' sau ``nu'', după cum maşina evaluată termină vreodată execuţia sau nu.
$\begin{figure}\centerline{\epsfxsize=10cm\epsffile{oprire.eps}}\end{figure}$

Teorema asta a fost demonstrată de Alan Turing, în 1936, deci cu mult înainte să existe calculatoarele în sensul modern al cuvîntului.

Demonstraţia teoremei opririi este extrem de simplă, şi se face prin reducere la absurd. Demonstraţia este extrem de înrudită cu celebrul paradox al mincinosului, cunoscut de grecii antici, care spune că fraza ``Eu mint'' nu poate fi nici adevărată, nici falsă, pentru că în orice caz s-ar auto-contrazice.

Să presupunem că există o maşină H, care rezolvă problema opririi. Atunci vom construi o nouă maşină, să-i spunem H1, care face următorul lucru:

Din moment ce H1 este o maşină Turing, putem să o descriem şi pe ea însuşi folosind un şir de caractere. Ce se întîmplă însă dacă pornim maşina H1 avînd pe banda de la intrare chiar propria ei descriere, de două ori, o dată pe post de M şi o data pe post de x?

Ei bine, dacă H1 se opreşte cu această intrare, atunci înseamnă că H1 va executa pasul (3) de mai sus, deci intră într-o buclă infinită, contradicţie!

Dacă H1 nu se opreşte niciodată, atunciH1 va executa pasul (4), deci se va opri imediat, altă contradicţie!

Aceste comportări sunt aberante, deci presupunerea noastră că H1 există trebuie să fie falsă; dar H1 este construită folosind H şi cîteva piese banale, deci H nu există!

Acest rezultat este extrem de important pentru practică. Aceasta ne spune că nu vom putea niciodată să verificăm automat corectitudinea oricărui algoritm, pentru că în general nu putem spune dacă un algoritm se va termina vreodată.

Consecinţe ale teoremei opririi

De asemenea, rezultă o serie întreagă de consecinţe foarte importante. Iată unele dintre ele, din perspectiva teoriei compilatoarelor:

Atenţie: nu vreau să spun că aceste lucruri sunt nedecidabile pentru orice program: e clar că două programe Pascal identice sunt echivalente. Ceea ce această teoremă spune, este că există programe pentru care aceste lucruri nu pot fi determinate.

Dacă restrîngem setul de programe pe care-l putem scrie, atunci putem desigur demonstra mai multe lucruri despre programele noastre. De exemplu, în limbajul Java, suntem asiguraţi de faptul că un program nu va accesa niciodată memorie nealocată, pentru că înainte de a verifica orice acces la memorie, maşina virtuală Java verifică dacă aceasta a fost alocată sau nu.

Dar e vorba de limbaje diferite de intrare: programele scrise în Java sunt un subset al tuturor programelor.

Semi-decidabilitate

După cum am văzut, există probleme pentru care nu putem niciodată calcula răspunsul.

Putem însă identifica printre problemele indecidabile o submulţime, a problemelor semi-decidabile, acele probleme pentru care putem calcula ``jumătate'' de răspuns: putem răspunde întotdeauna corect cînd suntem întrebaţi de o instanţă ``da'', dar cînd suntem întrebaţi de o instanţă ``nu'' s-ar putea să dăm răspunsul corect, sau s-ar putea să nu terminăm niciodată de calculat.

Problema opririi este de fapt o problema semi-decidabilă: dacă ni se dă o maşină M şi un şir x pentru care maşina se opreşte, vom fi capabili să descoperim acest lucru simulînd funcţionarea maşinii M cu intrarea x pînă atinge starea finală. Dacă M însă nu se opreşte cînd primeşte pe x, nici simularea nu se va termina niciodată.

Oracole

O întrebare interesantă este următoarea: sunt tot felul de probleme indecidabile; dar sunt cumva unele dintre ele mai grele decît altele? Poate să pară ciudat că întrebăm astfel de lucruri despre probleme pe care oricum nu le putem rezolva, dar răspunsul este şi mai surprinzător.

Contextul matematic pentru a formula aceste întrebări este numit al ``oracolelor''. Putem găsi o interpretare filozofică interesantă pentru acest gen de construcţii: să zicem că facem un pact cu diavolul, care ne va răspunde corect la anumite întrebări nedecidabile. De pildă, ne va da întotdeauna răspunsul corect la întrebări despre oprirea unei maşini Turing. Vedeţi, răspunsul există, orice maşină fie se opreşte, fie nu se opreşte, ceea ce nu există este o metodă de a calcula răspunsul. Să zicem că Mefistofel însă ne poate da răspunsul, folosind puterile sale supranaturale.

Vom vedea că noţiunea de oracol este foarte utilă nu numai atunci cînd vrem răspunsuri la întrebări nedecidabile, ci şi atunci cînd vrem răspunsuri la întrebări pentru care nu avem destule resurse. Mai multe despre asta în partea a doua a acestui articol, în numărul viitor al revistei.

Matematic, un oracol este o a doua bandă pentru maşina noastră, pe care sunt scrise dinainte răspunsurile (corecte!) la întrebările pe care maşina le pune (vedeţi figura 4).

**Figura 4:** Maşini cu Oracole: un oracol este o anumită funcţie pe care maşina nu o poate calcula, dar de care se poate folosi. Matematic modelăm oracolul printr-o bandă infinită, pe care sunt dinainte scrise răspunsurile corecte la toate întrebările pe care maşina le-ar putea pune. În general ne interesează să vedem ce ar putea face în mod suplimentar o maşina Turing dacă ar putea răspunde unor anumite întrebări (dar nu *oricărei* întrebări); atunci o echipăm cu un oracol care ştie toate răspunsurile la întrebările în chestiune.
$\begin{figure}\centerline{\epsfxsize=10cm\epsffile{oracol.eps}}\end{figure}$

Ierarhia aritmetică

Dacă avem un oracol, mai există lucruri pe care nu le putem calcula? Exista alte întrebări la care nu putem răspunde?

Ei bine, da. Există întrebări care sunt în continuare ne-decidabile. De exemplu, întrebarea ``este limbajul acceptat de maşina M finit'' nu poate fi elucidată nici în prezenţa unui oracol pentru problema opririi.

Dar dacă presupunem că avem un oracol care ne răspunde şi la această întrebare? Mai există şi altceva care nu se poate calcula? Din nou, răspunsul este ``da'': de exemplu nu putem răspunde nici acum la întrebarea ``este limbajul acceptat de maşina M co-finit'' (adică şirurile ne-acceptate sunt în număr finit).

Şi aşa mai departe: există o ierarhie infinită maşini de oracole din ce în ce mai puternice, care pot răspunde la aceste întrebări, dar care sunt neputincioase în faţa unor întrebări mai complicate. Această ierarhie de probleme ne-decidabile se numeşte ierarhia aritmetică.

Concluzii

Voi încheia aici prima parte a acestui articol. Subiectele prezentate aici pot fi caracterizate ca făcînd parte din pre-istoria teoriei complexităţii: sunt fapte cunoscute începînd din anii 1920 pînă prin deceniul şase al secolului nostru. În numărul următor din PC Report îmi voi apleca atenţia asupra evoluţiilor recente din domeniu, care sunt extrem de spectaculoase, şi voi privi cu mai multă atenţie problemele care se pot ataca avînd resurse limitate.

În textul de faţă am studiat mai mult problemele care nu se pot rezolva, oricît de multe resurse computaţionale am avea la dispoziţie, numite probleme indecidabile. Am văzut că foarte multe probleme practice sunt indecidabile; mai ales problemele care privesc programele însele.

Dar importanţa acestui articol constă mai ales în faptul că arată cum se pot formaliza foarte precis noţiunile de proces de calcul şi funcţie calculată de un program, în aşa fel încît să le putem supune ochiului scrutător al matematicii.

Alte surse de informaţie

Cititorilor care doresc să aprofundeze aceste subiecte le recomand următoarele cărţi:

Introduction to Automata Theory, Languages and Computation, J. E. Hopcroft and J. D. Ullman, Addison-Wesley, 1979.

Teoria clasică a complexităţii

Acest text este partea a doua a unui foileton despre teoria complexităţii, cea mai abstractă ramură a informaticii. Deşi încerc ca fiecare articol din serie să fie de sine-stătător, o vedere de ansamblu poate fi obţinută parcurgîndu-le pe toate; textele anterioare sunt disponibile (pe lîngă revista PC Report) şi din pagina mea de web.

Am consacrat acestei teme două texte în lunile octombrie şi noiembrie, despre problema satisfiabilităţii boolene, şi numărul din decembrie al revistei, care introducea obiectele de bază cu care operează teoria complexităţii, după care discuta despre calculabilitate.

Cu această ocazie vreau să fac şi o corectură: teorema pe care am prezentat-o în numărul anterior ca ``teorema găurii'' este de fapt numită teorema ierarhiei; enunţul teoremei găurii este altul, dar nu o să-l prezint aici.

Recapitulare

Voi reaminti cititorilor că teoria complexităţii discută despre ceea ce se poate calcula şi nu se poate calcula atunci cînd avem anumite resurse la dispoziţie. Teoria calculabilităţii discută cazul extrem al lucrurilor care nu se pot calcula deloc, chiar dacă avem la dispoziţie o cantitate infinită de resurse. În mod surprinzător, există foarte multe lucruri care nu se pot calcula, aşa cum am arătat în articolul anterior.

Pentru a putea discuta precis despre ce se poate calcula, teoria complexităţii operează cu nişte modele matematice ale maşinilor de calcul, descrise sub forma unor automate simple, care comunică cu lumea exterioară folosind nişte benzi pe care sunt scrise litere, şi care au o unitate de control cu un număr finit de reguli, care indică automatului care este pasul următor de făcut în fiecare circumstanţă.

Modelul cel mai ades folosit este cel al maşinii Turing, numite în cinstea marelui matematician englez, Alan Turing. Turing a fost unul dintre pionierii acestei teorii; el este însă mai cunoscut prin activitatea lui din al doilea război mondial, cînd a contribuit la spargerea cifrurilor maşinii Enigma, care cripta comunicaţiile Germaniei naziste. Munca lui Turing a permis aliaţilor să intercepteze informaţii foarte importante despre mişcările maşinii de război germane.

Turing era un matematician de excepţie, care studiase la Princeton cu Albert Einstein, şi colaborase cu John von Neumann, părintele american al calculatoarelor. Din nefericire soarta lui Turing a fost tragică: contribuţiile sale militare din al doilea război mondial au rămas confidenţiale pentru multă vreme; după război a fost condamnat pentru homosexualitate, şi forţat să urmeze un tratament hormonal, despre care autorităţile timpului credeau că poate ``vindeca'' această ``boală''. Influenţa medicamentelor şi umilirea îndurată însă au fost prea mult pentru Turing, care s-a sinucis înghiţind cianura, în 1954, la doar 42 ani. În cinstea sa, cel mai important premiu care recunoaşte contribuţiile în domeniul informaticii, decernat anual de prestigioasa asociaţie ACM (Association for Computing Machinery), este numit premiul Turing.

În mod interesant, deşi maşina Turing este un mecanism foarte ``primitiv'', nimeni nu a reuşit să sugereze un model de calcul mai puternic. În măsura în care funcţionarea neuronilor din creierul uman este cea descrisă de neurofiziologi, creierul însuşi poate fi simulat cu o maşină Turing (dar există mult mai multe necunoscute decît certitudini în ceea ce priveşte funcţionarea creierului). Dacă acceptăm această ipoteză (numită şi teza lui Church), putem privi rezultatele teoriei complexităţii ca pe nişte reguli universale, care privesc toate ``aparatele'' care procesează informaţie în univers.

Să ne mai amintim că obiectele procesate de maşinile Turing sunt limbaje, adică mulţimi de cuvinte. O maşină Turing primeşte la intrare un cuvînt dintr-un anumit limbaj, şi produce la ieşire un cuvînt dintr-un alt limbaj, care este răspunsul aşteptat. Dacă răspunsurile sunt doar ``da'' sau ``nu'' (adică un singur bit), atunci spunem că maşina Turing decide limbajul format din toate cuvintele pentru care răspunsul este ``da''.

Pietre de hotar

Putem împărţi istoria teoriei complexităţii, de la origini pînă în prezent, în cinci etape mari. Iată-le descrise pe scurt:

Programul formalist al lui Hilbert

Putem considera ca părinte al teoriei complexităţii pe marele matematician german David Hilbert (1862-1943). Hilbert a încercat să fundamenteze matematica pe baze axiomatice; el a recunoscut faptul că între logică şi matematică există o relaţie foarte strînsă; el a observat că demonstrarea oricărei probleme din matematică se poate reduce la verificarea satisfiabilităţii unei formule din calculul predicativ².

Hilbert vedea ca încununare a matematicii producerea unui algoritm care ar putea să rezolve problema satisfiabilităţii, care ar putea fi atunci folosit pentru a demonstra în mod mecanic orice teoremă.

Teorema lui Gödel şi teorema lui Turing

Visele lui Hilbert au fost însă spulberate de matematicianul Kurt Gödel şi faimoasa sa teoremă de incompletitudine. Gödel a arătat că un algoritm de decizie pentru satisfiabilitate nu există, pentru orice sistem axiomatic care este suficient de cuprinzător pentru a descrie mulţimea numerelor naturale şi operaţiile aritmetice pe ea. Dacă operăm cu structuri mai simple, ca algebra booleană, introdusă în articolul nostru despre satisfiabilitate, problema este decidabilă; dacă însă structura matematică este suficient de bogată, (şi mulţimea numerelor naturale este în definitiv o structură foarte simplă, fără de care cu greu putem vorbi de matematică evoluată), există propoziţii adevărate care nu pot fi demonstrate matematic. Voi clarifica într-un alt episod semnificaţia acestui enunţ.

O altă problemă fundamentală, propusă de Hilbert, era de a verifica dacă un sistem dat de axiome este consistent sau nu (cu alte cuvinte, dacă axiomele nu se contrazic între ele). De exemplu, ştim din liceu că axioma paralelelor a lui Euclid, din geometria plană, este independentă de celelalte axiome ale geometriei, şi că putem construi geometrii în care această axiomă este adevărată, precum şi geometrii perfect coerente în care axioma este falsă. Hilbert îşi dorea posibilitatea de a verifica dacă nu cumva un sistem ales de axiome se contrazice pe sine. A doua teoremă de incompletitudine a lui Gödel a sfărîmat şi acest vis al lui Hilbert, demonstrînd că este imposibil de demonstrat consistenţa unui sistem de axiome raţionînd doar în interiorul sistemului (cu alte cuvinte, nu putem demonstra consitenţa axiomelor pornind doar de la acele axiome); dacă vrem să facem acest lucru, trebuie să raţionăm într-un sistem mai cuprinzător decît cel studiat. Avem astfel o reducere infinită, pentru că putem pune apoi chestiunea consistenţei sistemului mai cuprinzător, etc.

Teorema lui Cook şi NP-completitudinea

Cu timpul oamenii s-au obişnuit cu ideea ca sunt lucruri care nu se pot calcula. Despre cele care se puteau calcula însă erau convinşi că sunt la-ndemînă. Teoria complexităţii însă a arătat că fiecare problemă are o complexitate inerentă; anumite probleme se pot rezolva repede, altele mai greu. Există probleme care au o complexitate exponenţială: dacă creşti datele de intrare cu o constantă, timpul de calcul se dublează. Astfel de probleme devin foarte repede intractabile: dacă creştem problema de 100 de ori, complexitatea creşte de 2¹⁰⁰ ori, depăşind astfel vîrsta estimată a universului! Chiar dacă începeam să calculăm la Big Bang, astăzi tot n-am fi terminat!

Teorema lui Cook, demonstrată în 1971, a turnat şi mai mult gaz peste foc: există foarte multe probleme care au soluţii simple, şi uşor de verificat (adică putem verifica foarte eficient dacă o pretinsă soluţie este corectă), dar pentru care nimeni nu ştie cum să găsească o soluţie suficient de rapid!

Din acel moment, problema centrală a teoriei complexităţii s-a mutat în această zonă: am renunţat să mai rezolvăm problemele inerent grele, putem oare măcar rezolva acest gen de probleme, ale căror soluţii se pot verifica uşor? Aceste probleme formează o clasă numită NP, despre care vom vorbi mai mult în cuprinsul acestui articol. Întrebarea centrală a teoriei complexităţii este dacă P=NP. (P este clasa problemelor pe care le putem rezolva rapid.)

S-au publicat mai multe demonstraţii eronate ale ambelor aserţiuni: P=NP şi P $\not=$ NP. Deocamdată răspunsul rămîne un mister. Teoreticienii au atacat problema din tot felul de perspective, încercînd să demonstreze că pentru problemele din NP sunt necesare strict mai multe resurse decît pentru cele din P; atunci am şti că cele două clase sunt diferite. Desigur, doar existenţa unei diferenţe între cele două clase nu este totul pentru practicieni, dacă nu ştim şi cît de mare este această diferenţă. Tot ce ştim este că NP este cuprinsă între P şi EXP; P este clasa problemelor cu o complexitate polinomială, iar EXP cea a problemelor cu complexitate exponenţială; între aceste două clase există o sumedenie de clase intermediare, de exemplu cea a problemelor cvasi-polinomiale, care sunt mai mari decît cele polinomiale, dar mai mici decît cele exponenţiale (de exemplu funcţia n^{log n}). Chiar un rezultat care ar separa NP de EXP ar fi grozav, pentru că ne-ar da soluţii pentru problemele din NP mai bune decît cunoaştem la ora actuală.

Teoreticienii aveau practic două scule fundamentale în repertoriu pentru a raţiona despre complexitate: diagonalizarea şi simularea, ambele prezentate pe scurt în prima parte a acestui articol, în numărul anterior al revistei.

Simularea se foloseşte de faptul că o maşină Turing adesea se poate comporta ca o altă maşină Turing, ``simulîndu-i'' execuţia. Această tehnică se numeşte în viaţa de zi cu zi ``interpretare'', şi este exact ceea ce se întîmplă cu limbajele interpretate: BASIC, Lisp, etc: interpretorul de BASIC simulează execuţia programelor scrise în BASIC.

Diagonalizarea este o tehnică foarte ingenioasă pentru a arăta că un obiect nu este într-o mulţime, pentru că este diferit de fiecare obiect din mulţime printr-o anumită trăsătură.

Teoreticienii au încercat să demonstreze că P $\not=$ NP arătînd că maşinile din NP sunt diferite de toate maşinile din P. Dar aceste încercări au fost brusc curmate de un rezultat şocant.

Teorema lui Solovay; relativizare

În 1977 logicianul Solovay a demonstrat o teoremă foarte importantă, care a arătat că orice metodă bazată pe diagonalizare şi simulare este sortită eşecului. Este deci un fel de meta-teoremă, care arată că o întreagă clasă de metode de demonstraţie sunt neputincioase în a diferenţia P de NP. Acest rezultat a paralizat complet cercetarea din domeniu pentru cîţiva ani. Voi încerca să prezint aici esenţa argumentului.

În episodul anterior am introdus noţiunea de maşină Turing echipată cu un oracol. Un oracol este un mecanism (fictiv) care permite unei maşini Turing să rezolve anumite probleme instantaneu. Putem vedea un oracol ca pe o subrutină, care se termină instantaneu, şi care poate calcula răspunsul la o anumită întrebare. De exemplu, un oracol pentru problema primalităţii unui număr este un dispozitiv care ne spune instantaneu dacă numărul este prim sau nu.

În acelaşi fel, un oracol pentru clasa NP este un dispozitiv care răspunde instantaneu la orice întrebare din clasa NP. Dacă vă deranjează această abstracţie matematică, imaginaţi-vă că este o subrutină oricît de complicată, dar al cărei timp de execuţie nu se cronometrează. Deşi abstracte, oracolele sunt nişte scule foarte utile pentru teorie, după cum vom vedea din teorema lui Solovay.

Mai introducem o notaţie: dacă o maşină Turing M are un oracol pentru problema X, atunci notăm maşina cu M^X. Asta înseamnă deci că M poate calcula ca orice maşină Turing obişnuită, dar în plus poate răspunde imediat la orice întrebare din X.

Teorema lui Solovay arăta că există două oracole A şi B care au următoarele proprietăţi: P^A = NP^A, dar ${\bf P}^B \not= {\bf NP}^B$ . Asta înseamnă că există oracole care fac maşinile din NP mai puternice decît cele din P, şi există oracole care fac ambele tipuri de maşini la fel de puternice.

De ce este această teoremă catastrofală? Pentru că s-a arătat că orice argument bazat pe diagonalizare sau simulare rămîne adevărat atunci cînd maşinilor li se aplică oracole. Cu alte cuvinte, dacă arătăm prin diagonalizare că o maşină X nu este într-o anumită clasă C, atunci pentru orice oracol Q vom şti sîcă X^Q nu este în clasa C^Q. Acest fenomen se numeşte relativizare: teoremele care sunt demonstrate prin diagonalizare sau simulare sunt adevărate şi atunci cînd maşinile din teoremă capătă oracole, deci teoremele sunt adevărate relativ la orice oracol.

Acum este clar de ce teorema a fost o veste foarte proastă: nu avem nici o şansă să arătăm cu aceste tehnici că P = NP, pentru că aplicînd oracolul B de mai sus, am arăta automat că P^B = NP^B, ceea ce e nu poate fi adevărat, conform teoremei lui Solovay. La fel stau lucrurile şi pentru propoziţia opusă: ${\bf P}\not= {\bf NP}$ nu poate fi demonstrată prin aceste tehnici, pentru că oracolul A ar contrazice acest rezultat.

Teorema lui Razborov-Rudich; demonstraţii naturale

Mulţi cercetători au fost foarte descurajaţi de acest rezultat, şi au abandonat studiul teoriei complexităţii cu totul. Toate sculele pe care le aveau la dispoziţie erau inutile! Încetul cu încetul însă comunitatea şi-a ieşit din apatie, şi o nouă tehnologie de demonstraţie a fost dezvoltată. Ultima parte a acestui articol va discuta despre această tehnologie mai pe larg, dar o să o introduc aici pe scurt.

Este clar că metoda care este folosită nu trebuie să sufere de relativizare, pentru că atunci conform teoremei lui Solovay ea este neputincioasă în a diferenţia P şi NP.

Cercetătorii au început atunci să opereze cu un alt model computatîonal, cel al circuitelor neuniforme. Acestea nu sunt altceva decît nişte circuite combinaţionale, precum cele folosite în construcţia calculatoarelor, formate din porţi logice ``sau'', ``şi'', ``nu''. Circuitele acestea primesc datele la intrare, şi generează răspunsul la ieşire. Pentru fiecare mărime de date de intrare avem de-a face cu un alt circuit: pentru datele de intrare de mărime 2 vom avea un circuit cu două intrări, pentru datele de mărime 3 vom avea un circuit cu 3 intrări, etc³.

Cercetarea părea să fie pe calea cea bună; cercetătorii vroiau să demonstreze că P $\not=$ NP arătînd că circuitele pentru probleme NP au nevoie de nişte proprietăţi suplimentare pentru a putea calcula, comparat cu cele din clasa P; de exemplu sperau să arate că orice problemă din P se poate rezolva cu circuite de o anumită ``adîncime'', pe cînd pentru NPeste nevoie de mai mult de atît.

Rezultatele curgeau unul după altul, aparent apropiindu-se de ţină. O lovitură de teatru însă a urmat în 1994: matematicianul rus Razborov şi americanul Steven Rudich au demonstrat o a doua teoremă de relativizare, care a avut un şoc comparabil cu cel al teoremei lui Solovay. Această teoremă este tehnic mai complicată decît cea a lui Solovay, dar voi încerca să expun aici esenţa ei.

Teorema Razborov-Rudich introduce noţiunea de demonstraţii ``naturale'' (natural proofs), care manipulează circuitele boolene într-un anumit fel. Apoi cei doi trec în revistă toate rezultatele majore şi arată că demonstraţiile folosite sunt naturale, sau echivalente cu demonstraţii naturale.

Apoi cei doi demonstrează un rezultat foarte interesant, pe care îl voi parafraza simplificat: dacă există probleme în NP mai grele decît cele din P (adică P $\not=$ NP), atunci nu exista demonstraţii naturale că P $\not=$ NP! Cu alte cuvinte, dacă faptul pe care vrei să-l demonstrezi este adevărat, atunci nu poţi să-l demonstrezi, cel puţin nu în acest fel!

Situaţia actuală

Aceasta este situaţia la ora actuală în teoria complexităţii. Cel puţin pe frontul P=NP, activitatea este din nou înţepenită: în lipsa unei tehnici noi de demonstraţie, orice efort este sortit dinainte eşecului!

Desigur, aşa cum arată teorema de incompletitudine a lui Gödel, în orice sistem axiomatic există teoreme adevărate care nu pot fi demonstrate. Este posibil ca chiar teorema P $\not=$ NP să fie o astfel de teoremă! Mai precis, este posibil ca acest enunţ să fie independent de teoria axiomatică a mulţimilor Zermelo-Frankel. Atunci clar nu există nici o demonstraţie a acestui fapt (ori a opusului lui), şi singurul lucru pe care-l putem face este să luăm un astfel de enunţ ca pe o axiomă!

Mulţi cercetători însă cred că această problemă nu este independentă, şi speră în continuare să găsească un răspuns. Pe ce cale se va face aceasta, la ora actuală este complet neclar.

Reduceri şi completitudine

În restul acestui articol ne vom ocupa de a doua perioadă din istoricul de mai sus; vom vedea o sumă de rezultate obţinute de teoreticieni, vom studia impactul a trei tipuri de resurse asupra calculului: spaţiul, timpul şi oracolele, şi vom vedea o serie întreagă de probleme nerezolvate, unele de o mare importanţă practică.

Vom introduce pentru început două noţiuni fundamentale în teoria complexităţii: cea de reducere între probleme şi cea de completitudine a unei probleme într-o clasă de complexitate.

Reduceri

Am întîlnit noţiunea de reducere şi în textul meu anterior despre problema satisfiabilităţii. De data asta vom studia însă un caz mai general.

Noţiunea de reducere este foarte ades folosită în matematică, unde spunem în mod frecvent că ``o problemă transformată într-un anume fel se reduce la o alta''. În teoria complexităţii reducerea este însă tot un proces de calcul, care transformă instanţe ale unui probleme în instanţe ale alteia. Ca orice procesare făcută de automatele de care ne interesăm, reducerile transformă un limbaj într-altul.

În teoria complexităţii ne interesează foarte mult şi cît de multe resurse consumă procesul de reducere. În general vrem ca reducerea însăşi să fie mai simplă decît problema iniţială sau cea finală; degeaba reducem o problemă de complexitate polinomială la alta dacă reducerea consumă un timp exponenţial!

Dacă problema A se reduce la problema B folosind o reducere de complexitate m, notăm acest fapt cu $A \leq_{m} B$ . Folosirea semnului $\leq$ (mai mic sau egal) nu este întîmplătoare: în general o reducere induce o relaţie de ordine pe mulţimea problemelor, fiind reflexivă (o problemă se reduce la sine însăşi) şi tranzitivă (dacă $A \leq_m B$ şi $B \leq_m C$ , atunci $A \leq_m C$ ). Dacă două probleme se reduc una la alta, spunem că sunt la fel de grele: $A \leq_m B$ şi $B \leq_m A$ , atunci A e la fel de grea ca B (aceasta este proprietatea de antisimetrie a relaţiei). În general proprietatea de simetrie nu este adevărată: dacă A se reduce la B, B nu se reduce neapărat la A; B poate să fie mai grea decît A.

Odată ce avem o noţiune de reducere, putem defini completitudinea unei probleme referitoare la o clasă. Dacă avem colecţia de probleme X, şi o problemă $A \in X$ , atunci spunem că A este completă în X, sau A este X-completă, vis-a-vis de o reducere cu complexitatea m, dacă pentru orice problemă $B \in X$ , $B \leq_m A$ .

**Figura 5:** În această figură mulţimea de probleme A are un set de probleme C care sunt A-complete. Asta înseamnă că rezolvarea oricărei probleme din A se reduce la o problemă din C. Dacă A include o sub-clasă B, atunci dacă B se intersectează cu C, atunci B=A, în sensul că ambele clase sunt la fel de grele. Singura posibilitate ca B sa fie diferit de A este ca B sa nu se intersecteze cu C. Aceste relaţii stau la baza multor încercări de a demonstra ca P = NP(sau opusul).
$\begin{figure}\centerline{\epsfxsize=2.3cm\epsffile{completitudine.eps}}\end{figure}$

Clase de complexitate importante

Deocamdată punem deoparte noţiunea de reducere, şi discutăm clasele de complexitate cele mai importante studiate. Pentru fiecare din aceste clase se cunosc probleme complete. Vom prezenta clasele în ordinea crescătoare a complexităţii lor; cel mai adesea însă relaţia reală între clase consecutive este necunoscută.

Spaţiu constant

Prima clasă interesantă de complexitate este cea a maşinilor care folosesc o cantitate fixă de spaţiu pentru a-şi face calculele, care cantitate este independentă de mărimea datelor de intrare. Chiar cînd datele de intrare tind la infinit, maşina foloseşte la fel de puţin spaţiu.

Un fapt interesant despre această clasă este că, de fapt, dacă dai unei maşini spaţiu constant, nu are ce face cu el: există o altă maşină care face acelaşi lucru fără nici un fel de spaţiu suplimentar. Există un nume special pentru maşinile Turing care nu folosesc nici un fel de spaţiu pe bandă (în afară de a citi şirul de la intrare): ele se numesc automate finite.

Toate limbajele care se pot decide în spaţiu constant se numesc limbaje regulate. Aceste limbaje sunt extrem de importante în practică; există o seamă întreagă de medii de programare care manipulează limbaje regulate. Programe şi interpretoare faimoase care manipulează limbaje regulate sunt Perl, Lex, grep, awk, sed, etc. Perl este de pildă limbajul preferat pentru a scrie extensii pentru serverele de web de pe Internet.

Limbajele regulate sunt atît de utile pentru că se demonstrează că ele pot fi acceptate în timp linear: cu alte cuvinte pentru orice limbaj regulat există o maşină Turing care decide un cuvînt de lungime n în timp O(n). Acest timp este practic cel mai mic timp posibil, pentru că în mai puţin de O(n) nu putem nici măcar citi toate literele de la intrare!

Un exemplu de limbaj regulat ne-trivial: adunarea. Dacă primim trei numere, a, b, c, scrise întreţesut pe bandă (adică o cifră de la a, una de la b, una de la c, atunci putem verifica folosind un automat finit dacă c = a+b.

Spaţiu logaritmic

O clasă foarte interesantă de complexitate este cea a limbajelor care pot fi acceptate folosind spaţiu logaritmic în lungimea cuvîntului de intrare. Pentru orice cuvînt de lungime n maşina foloseşte nu mai mult de O(log n) celule de memorie pentru a procesa cuvîntul.

Clasa aceasta se notează cu L, de la Logaritm. Se arată că această clasă este strict mai cuprinzătoare decît cea a limbajelor regulate: există limbaje ne-regulate în L.

De ce folosim tocmai logaritmul? În spaţiu logaritmic maşina poate manipula un număr finit de contoare a căror valoare este cuprinsă între 1 şi n (fiecare contor are log n cifre). Putem spune deci că clasa L este cea a maşinilor care au nevoie doar să ţină minte cîteva poziţii din şirul de intrare, şi nimic mai mult.

Ce putem face în spaţiu logaritmic? O mulţime de lucruri! De pildă putem înmulţi două numere: folosim contoare pentru a parcurge numerele de înmulţit, şi pentru a face adunarea de la dreapta la stînga.

O altă problemă foarte importantă pe care o putem rezolva doar în spaţiu logaritmic este de a calcula valoarea unei formule boolene, atunci cînd cunoaştem valorile tuturor variabilelor care o compun.

Timp polinomial

Cea mai folosită clasă de complexitate este cea a timpului polinomial, notată cu P. Putem defini foarte precis P matematic folosind următoarea notaţie TIME(f(n))= clasa problemelor care se pot decide în timp f(n). Atunci ${\bf P}\ = \cup_{k \in N} TIME(n^k)$ .

Se arată imediat că orice se poate calcula în spaţiu logaritmic, nu are niciodată nevoie de mai mult decît timp polinomial, sau altfel spus, ${\bf L}\ \subseteq {\bf P}$ .

Practic toţi algoritmii eficace învăţaţi în şcoală sunt din clasa P; teoreticienii consideră că dacă o problemă nu este în P, atunci nu poate fi rezolvată practic, pentru că resursele cerute sunt prea multe. De exemplu, programarea lineară, algoritmul Gauss-Seidel de inversare a unei matrici, sau algoritmul care calculează ieşirea unui circuit combinaţional cînd intrarea este dată, sunt toţi algoritmi de timp polinomial.

De fapt ultima problemă este chiar P-completă, vis-a-vis de reduceri în spaţiu logaritmic. Deci orice altă problemă din P se poate reduce la problema evaluării unui circuit boolean! Observaţi că evaluarea unui circuit boolean este mai dificilă decît a unei formule boolene, deşi orice formulă boolean poate fi scrisă ca un circuit.

Relaţia exactă dintre L şi P nu este cunoscută; nu se ştie dacă L este strict inclusă în P sau cele două clase sunt de fapt egale. Dacă cineva ar găsi o metodă de a rezolva problema valorii unui circuit boolean folosind un algoritm din L, atunci am demonstra automat că L = P, datorită completitudinii problemei.

Această întrebare este foarte importantă pentru practică, pentru că algoritmii din L pot fi asimilaţi cu algoritmii care se pot executa foarte eficient pe o maşină masiv paralelă. Chestiunea L = P se poate deci interpreta ca întrebarea: ``poate orice algoritm din P fi executat foarte eficient în paralel?''.

Spaţiu polinomial

În general este uşor de văzut că dacă o problemă are nevoie de timp t atunci nu consumă mai mult de spaţiu t, pentru că în fiecare unitate de timp poate consuma cel mult o unitate nouă de spaţiu. Dacă notăm cu PSPACE clasa problemelor care consumă spaţiu polinomial în mărimea datelor de intrare, atunci avem deci imediat P $\subseteq$ PSPACE.

Ce putem rezolva avînd la dispoziţie spaţiu polinomial? Ei bine, putem rezolva toate jocurile cu informaţie perfectă. Mai mult decît atît, aceste probleme sunt PSPACE-complete vis-a-vis de reduceri în timp polinomial. Ce sunt jocurile cu informaţie perfectă? Sunt toate jocurile gen Go sau dame pe table de mărime n x n (aceasta este mărimea datelor de intrare). Aş spune şah, dar este destul de greu de generalizat şah-ul pentru table arbitrar de mari.

Aşa cum ştim din teoria jocurilor (sau dacă nu ştim, vă spun eu), orice joc de acest gen are o strategie perfectă pentru fiecare jucător, care obţine cel mai bun rezultat, independent de mişcările celuilalt. Problema de a afla dacă primul la mutare poate cîştiga mereu este cea a jocurilor cu informaţie perfectă.

În mod surprinzător (sau poate v-aţi obişnuit cu aceste întrebări nerezolvate, şi vi se pare naturală ignoranţa noastră în acest domeniu), nimeni nu ştie dacă P= PSPACE. Ceea ce ştim cu siguranţă este că L $\subset$ PSPACE este o incluziune strictă.

Interesant, anumite probleme practice foarte utile sunt de asemenea PSPACE-complete; de exemplu problemele de planificare care apar în inteligenţa artificială, cum ar fi programarea traseului unui robot. O altă problemă importantă care este completă pentru PSPACE este problema pe care o întîlnesc cei care scriu compilatoare atunci cînd analizează un program cu pointeri pentru un limbaj ca C, care permite crearea de pointeri către funcţii: determinarea la compilare a informaţiei ``points-to'', care spune spre care obiecte un pointer poate arăta, este şi ea completă pentru PSPACE.

Timp exponenţial

Deşi nu am arătat cum, acelaşi gen de demonstraţie care arată că L $\subseteq$ P poate fi folosit pentru a arăta că PSPACE $\subseteq$ EXP. EXP este definită ca fiind clasa tuturor problemelor care se rezolvă în timp exponenţial: ${\bf EXP}= \cup_{k \in N} TIME(2^{n^k})$ .

Nu avem habar dacă incluziunea PSPACE $\subseteq$ EXP este strictă sau nu.

Spaţiu exponenţial

Dacă putem folosi timp exponenţial, putem folosi şi spaţiu exponenţial. Această clasă monstruoasă este puţin întîlnită în practică, deşi există probleme practice care pot fi plasate aici.

Dincolo de spaţiu exponenţial

Există şi clase de complexitate mai mari decît acestea. Vom prezenta o astfel de clasă în ultima parte a acestui text, într-un număr ulterior, cînd discutăm despre complexitatea de decizie a feluritelor teorii logice.

Complexitatea nedeterministă; maşini alternante

Modelul de maşină cu care am lucrat pînă acum este destul de realist, în sensul că pare imediat construibil în practică. Singura ciudăţenie abstractă au fost oracolele.

Dar aşa cum modelul ezoteric al oracolelor, deşi ne-implementabil, a fost de o enormă importanţă metodologică, permiţindu-ne să tragem nişte concluzii foarte importante, teoreticienii au mai elaborat două variaţiuni la modelul maşinilor Turing, care se dovedesc extrem de importante în practică.

Modelele pe care le voi introduce acum pot fi simulate cu maşini Turing obişnuite, cu o pierdere oarecare de eficacitate. Dar prezenţa acestor maşini ne permite să facem nişte diviziuni mai fine în interiorul feluritelor clase de complexitate, şi să punem nişte întrebări foarte importante.

Maşini nedeterministe

Vă reamintiţi că definiţia maşinii Turing spunea exact ce trebuie să facă automatul în fiecare stare, în funcţie de simbolul de pe bandă. Ei bine, acum vom permite o oarecare ambiguitate: maşina noastră va avea posibilitatea să facă nu una, ci mai multe mişcari la un moment dat.

Trebuie să redefinim conceptul de acceptare: înainte maşina accepta dacă secvenţa ei de stări parcurse se termina cu o stare anumită, numită ``acceptare''. Dar acum, cînd maşina poate urma mai multe trasee, care este criteriul de acceptare? Vom spune că maşina acceptă atunci există cel puţin o cărare care duce la o acceptare.

**Figura 6:** O maşină deterministă, de îndată ce are un şir pe banda de intrare, are o traiectorie fixată în spaţiul stărilor: putem spune oricînd în ce stare maşina se va afla. Prin contrast, maşinile nedeterministe se pot afla în stări cu mai mulţi succesori, în care pot alege traiectoria. O maşină deterministă acceptă dacă cel puţin o traiectorie a ei accepta.
$\begin{figure}\centerline{\epsfxsize=11cm\epsffile{nedeterminism.eps}}\end{figure}$

Intuitiv putem să ne imaginăm astfel de maşini în două feluri; alegeţi-l pe cel preferat:

Maşinile nedeterministe le generalizează pe cele deterministe; par de asemenea mai puternice: e clar că orice problemă care se poate executa în timp determinist T se poate executa şi în timp nedeterminist T, pentru că orice maşina deterministă este un caz particular de maşină nedeterministă.

Apar astfel clasele de complexitate prefixate cu litera N: NL, NP, NPSPACE, NEXP. De asemenea, o clasă nedeterministă este mai slabă decît clasa deterministă superioară: avem ierarhia: $\L \subseteq {\bf NL}\subseteq {\bf P}\subseteq {\bf NP}\subseteq {\bf PSPACE}\subseteq {\bf NPSPACE}\subseteq {\bf EXP}\subseteq {\bf NEXP}$ . Despre majoritatea incluziunilor din acest lanţ nu ştim dacă sunt stricte.

Un singur rezultat pozitiv luminează aceste incertitudini: în mod surprinzător în 1970 Savitch a demonstrat că PSPACE= NPSPACE, deci nedeterminismul nu ajută cu nimic puterea computaţională pentru acest gen de probleme.

În plus mai ştim adesea că anumite incluziuni între clase distante sunt stricte: de exemplu avem teoreme de genul ``fie L $\not=$ P, fie P $\not=$ PSPACE'', sau, mai simplu spus, ${\bf L}\not= {\bf PSPACE}$ .

Aşa cum am mai menţionat, clasa asupra căreia s-au aplecat cei mai mulţi cercetători este NP. Articolele mele anterioare arătau că problema satisfiabilităţii boolene (``are un circuit boolean intrări pentru care ieşire este 1'') este completă pentru NP vis-a-vis de reduceri polinomiale.

O să menţionez în final o problemă completă pentru NEXP: jocul de poker generalizat în trei adversari (jocuri în mai multe persoane, cu aleatorism şi informaţie ascunsă).

Clase complementare

O întrebare naturală este: dacă putem generaliza maşina Turing să aibă astfel de stări în care poate face o alegere, nu putem crea şi nişte stări speciale în care orice alegere să trebuiască să ducă la o stare acceptoare? În modelul paralel, cu fire de execuţie, cerem ca toate firele lansate în paralel să termine cu succes, şi nu unul singur dintre ele.

Vom distinge deci două tipuri de stări: stările existenţiale: cel puţin o cărare care iese din ele trebuie să ducă la o acceptare (acestea sunt stările din maşinile nedeterministe, introduse mai sus), şi stările universale: toate cărările plecînd din acea stare trebuie să ducă la o acceptare.

Într-adevăr, aceste maşini recunosc alte clase de limbaje. O maşina care are doar stări universale recunoaşte anumite clase de limbaje interesante. Se poate arăta că aceste limbaje sunt complementele limbajelor acceptate de maşinile nedeterministe, de aceea numele lor se prefixează cu ``Co''. De exemplu, avem clasa limbajelor CoL, care pot fi acceptate de o maşină cu stări universale în spaţiu logaritmic. Avem CoNP, limbajele care pot fi acceptate de maşinile polinomiale cu stări universale.

Din nou, maşinile perfect deterministe sunt un caz particular de maşini cu stări universale, în care în fiecare stare avem o singură decizie posibilă. De aici rezultă imediat o serie de incluziuni: ${\bf L}\subseteq {\bf NL}\cap Co{\bf NL}$ , ${\bf P}\subseteq {\bf NP}\cap Co{\bf NP}$ , etc.

Ca să fim mai concreţi, să vedem o problemă care este în CoNP. Problema este foarte interesantă: dacă am două hărţi, sunt ele ne-izomorfe? Adică, oricum aş asocia ţările dintr-una cu ţările din cealaltă, nu voi obţine niciodată aceeaşi relaţie de vecinătate (dacă sunteţi familiari cu terminologia grafurilor, aceasta este de fapt problema non-izomorfismului grafurilor).

Această problemă este în CoNP, pentru că vreau să verific că orice permutare a unei hărţi este diferită de cealaltă. Putem deci construi o maşină cu o stare universală, din care se explorează în paralel toate permutările posibile.

Vedeţi, problema cealaltă, a izomorfismului grafurilor este în NP: ``sunt două grafuri izomorfe?'' se poate rezolva în timp nedeterminist polinomial. Complementul acestei probleme este însă în CoNP. E interesant de observat că adesea o problemă nu este la fel de grea ca problema complementară. De pildă, e uşor să demonstrezi că nu a plouat peste noapte: străzile sunt uscate. Dar dacă străzile sunt ude, nu poţi să ştii dacă nu cumva au spălat strada. Un lucru şi complementul lui nu sunt la fel de uşor de demonstrat.

De fapt aici nu am exprimat decît o credinţă: relaţia dintre clasele de complexitate şi complementele lor este cel mai adesea necunoscută; singurul rezultat concret este dat teorema Immerman-Szelepcsényi, din 1988, care arăta că NL= CoNL.

Întrebarea NP= CoNP este o întrebare cu consecinţe foarte importante pentru practică; dacă aceste clase sunt egale (ceea ce lumea crede foarte puţin probabil), atunci există demonstraţii scurte pentru non-izomorfismul grafurilor: poţi scrie o dovadă sumară că două grafuri nu sunt identice.

Maşini alternante, ierarhia polinomială

Putem generaliza şi mai departe maşinile Turing, permiţindu-le să aibă simultan stări existenţiale şi universale. În acest fel obţinem noi clase de complexitate. Ceea ce caracterizează aceste maşini nu este numărul de stări de fiecare fel, ci numărul de alternanţe de stări pe fiecare cărare. De exemplu, dacă avem o stare existenţială, urmată apoi pe fiecare ramură de stări universale, şi doar atît, avem o alternanţă 2. Cu cît permitem mai multe alternanţe, cu atît maşina pare mai puternică.

În mod interesant, putem modela aceste maşini şi folosind oracole. O maşină care face o alternanţă existenţială urmată de una universală poate fi modelată de o maşină din NP care are un oracol din CoNP. Oracolul poate răspunde la orice întrebare universală, iar maşina ia doar o decizie existenţială. Putem nota această maşină cu ${\bf NP}^{Co{\bf NP}}$ .

Se definesc astfel clasele $\Pi_k = Co{\bf NP}^{\Pi_{k-1}}$ şi $\Sigma_k = {\bf NP}^{\Sigma_{k-1}}$ ; punctul de pornire este $\Sigma_1 = {\bf NP}$ . Figura 7 ilustrează relaţia dintre aceste probleme. O problemă din $\Pi_k$ are un număr de k alternanţe, şi prima stare este peste tot una universală. O problemă din $\Sigma_k$ are tot k alternanţe, dar prima stare pe orice cărare este una existenţială. Figura 7 ilustrează această ierarhie de dificultăţi, numită ``ierarhia polinomială''.

Din nou, nu se cunoaşte nimic despre stricteţea incluziunilor. Se ştie însă că dacă pentru un k anume $\Sigma_k = \Sigma_{k+1}$ , atunci acest lucru este adevărat pentru oricare număr mai mare decît k: ierarhia se prăbuşeşte la nivelul k: $\Sigma_j = \Sigma_k \forall j > k$ . Totalitatea tuturor acestor clase pentru k constant se notează cu PH $=\cup_i \Sigma_i$ . Dacă mergem mai departe, şi îi permitem şi lui k să varieze odată cu dimensiunea problemei, atingem PSPACE.

Pentru fiecare dintre aceste clase de complexitate există probleme care sunt complete prin reduceri polinomiale. De exemplu, iată un limbaj complet pentru $\Pi_2$ : limbajul format din descrierea tuturor circuitelor booleene care au numărul minim de porţi care implementează o anumită funcţionalitate.

**Figura 7:** Ierarhia polinomială PH. Aproape nici una dintre incluziunile din această figură nu sunt demonstrate a fi stricte. Lumea crede că într-adevăr relaţia este cea din figură. ER sunt limbajele regulate, L=spaţiu logaritmic, P=timp polinomial. Celelalte clase sunt definite in text.
$\begin{figure}\centerline{\epsfxsize=11cm\epsffile{polinomiala.eps}}\end{figure}$

Concluzii

În acest text am văzut ca nu tot ce se poate calcula în mod necesar se poate calcula repede: există clase de complexitate foarte ``grele''.

Am mai văzut că modelele matematice abstracte ale maşinilor cu oracole, maşinilor nedeterministe şi maşinilor alternante sunt nişte scule foarte puternice pentru a explora structura diferitelor probleme din punct de vedere al complexităţii. Am mai văzut că există clase de complexitate extrem de variate, şi populate de probleme foarte interesante: am văzut de pildă clasa problemelor care se pot paraleliza foarte eficient, L, clasa PSPACE a jocurilor, care este (probabil) mult mai grea decît clasa problemelor tractabile, şi clase nedeterministe şi alternante, care formează o ierarhie infinită de obiecte din ce în ce mai greu de calculat.

În episodul următor vom ataca subiecte şi mai stranii: vom vorbi despre complexitatea circuitelor ne-uniforme, şi vom vedea cum se pot formaliza foarte precis noţiunile de criptare, pseudo-aleatorism şi calcul bazat pe întîmplare. Pe luna viitoare!

Aleatorism şi complexitate

Acest text este un al treilea episod consacrat teoriei complexitătii. În oarecare măsură el este independent de episoadele anterioare sau ulterioare, dar pentru cititorul doritor de o privire de ansamblu, celelalte părţi sunt disponibile din pagina mea de web.

Teoria complexităţii este ramura cea mai abstractă a informaticii teoretice, care studiază ce se poate şi nu se poate calcula, atunci cînd punem tot felul de constrîngeri asupra resurselor de calcul pe care le avem la dispoziţie.

În primul text din această serie, am discutat despre teoria extremă a calculabilităţii, care investighează lucruri care nu se pot calcula oricît de multe lucruri am avea la dispoziţie. În mod surprinzător, există mult mai multe lucruri ne-calculabile decît calculabile; există deci o infinitate de lucruri pe care nu le vom putea dovedi niciodată.

Al doilea episod a investigat cum se schimbă peisajul lucrurilor calculabile dacă restrîngem timpul pe care i-l punem la dispoziţie unui calculator, respectiv spaţiul de memorie pe care-l poate folosi. Am văzut că există probleme deosebit de interesante pentru care este necesară o cantitate foarte mare de resurse, de exemplu jocurile între doi jucători. Am văzut însă că se pot calcula lucruri foarte interesante chiar dacă avem 0 resurse de memorie, şi foarte puţin timp la dispoziţie: acestea sunt limbajele regulate⁴, care au foarte multe aplicaţii practice.

Acest al treilea episod are drept personaj central un tip foarte surprinzător de resursă de calcul: aleatorismul. Toate clasele de complexitate prezentate în acest text sunt bazate în mod fundamental pe aleatorism.

Aleatorism (randomness) şi amplificare (boosting)

Ce este aleatorismul în teoria complexităţii, şi cum îl putem modela? Cum putem introduce în modelul simplu de calcul pe care l-am folosit, al maşinii Turing, aleatorism?

Despre ce e aleatorismul în viaţa de zi cu zi, şi cum poate fi el produs, sunt încă dezbateri aprinse între filozofi. Noi vom lua drept bună o sursă foarte simplă de aleatorism: un ban cu două feţe (diferite). Vom presupune că banul este perfect echilibrat, şi că odată aruncat, poate ateriza cu aceeaşi probabilitate, de 1/2, pe oricare dintre feţele sale. Astfel, o fisă ne oferă de fiecare dată cînd este aruncată un bit aleator: un ``0'' sau un ``1'', fiecare cu probabilitate 1/2. Presupunem de asemenea ca între aruncări independente ale banului nu există nici o relaţie (adică ele sunt independente): presupunem că faptul că banul a aterizat de zece ori la rînd cu faţa ``1'' în sus nu face mai probabilă apariţia ulterioară a unei feţe ``0''. Unii filozofi şi ``bunul simţ'' al foarte multor inşi nu vor fi de acord cu aceste presupuneri, dar acesta este luxul matematicii: putem face orice presupuneri, atîta vreme cît le enunţăm clar.

Atunci cînd modelăm matematic aleatorismul pentru o maşină Turing, ne imaginăm că cineva a dat dinainte cu banul şi a înscris pe o bandă infinită rezultatele aruncărilor. Această bandă este disponibilă maşinii Turing, care de fiecare dată cînd are nevoie de un bit aleator, citeşte un bit de pe această bandă. Această bandă, cu biţi aleatori, nu poate fi decît citită, iar capul de citire nu se poate niciodată întoarce înapoi. Aşa cum am zis, biţii de pe bandă sunt uniform distribuiţi (adică 0 şi 1 apar fiecare cu probabilitate 1/2) şi independenţi unul de altul.

În general, atunci cînd introducem aleatorism în calcul, pierdem certitudinea. Putem pierde certitudinea în două feluri diferite: în primul fel, s-ar putea ca rezultatele calculate de algoritm să fie eronate. În al doilea fel, s-ar putea ca rezultatele să fie sigur corecte, dar să nu fie clar cît de repede algoritmul termină execuţia. Cum de putem tolera aşa ceva? Ce ne facem cu calculatoarele, dacă întrebăm cît fac 7*9 şi din cînd în cînd primim răspunsul 62? Ce încredere mai putem avea în algoritmi, atunci cînd ei nu sunt 100% fiabili?

Acestea sunt întrebări foarte legitime; avem însă la dispoziţie o tehnică remarcabil de simplă prin care putem spori arbitrar certitudinea unui rezultat. Această tehnică se numeşte aplificare (boosting), şi constă în repetarea de mai multe ori a unui calcul incert⁵.

Ideea este destul de simplă şi uşor de demonstrat matematic. Voi argumenta insă în cuvinte: să presupunem că facem un experiment care are şansa să iasă prost cu o probabilitate mică, dar ne-nulă (neapărat mai mică de 1/2). Atunci, dacă repetăm experimentul de 20 de ori, probabilitatea ca mai mult de 10 experimente să iasă prost este foarte mică. Soluţia este deci de a repeta experimentul, şi de a considera răspunsul corect pe cel care apare majoritar. Probabilitatea de a greşi în acest fel scade în mod exponenţial cu numărul de repetiţii. Scăderea aceasta foarte rapidă este esenţială: este suficient să facem un număr relativ mic de repetiţii pentru a reduce probabilitatea la o valoare infimă. Un lucru foarte important este că adesea numărul de repetiţii pe care trebuie să-l facem nu depinde de mărimea problemei pe care o rezolvăm. Vă reamintesc că timpul de execuţie al unui algoritm depinde practic întotdeauna de mărimea datelor de intrare; dacă însă probabilitatea de eşec a unui algoritm aleator este independentă de mărimea datelor de intrare (şi cel mai adesea, este), atunci numărul de repetiţii este constant, acelaşi, indiferent de cît de mare este problema!

Din punct de vedere practic algoritmii aleatori sunt perfect tolerabili: putem reduce probabilitatea de eroare atît de mică încît să fie mai probabil ca între timp calculatorul însuşi să se strice, sau astfel încît să fie mai probabil că se va produce o calamitate de mari proporţii, după care rezultatele calculului vor mai interesa pe foarte puţină lume.

Complexitate probabilistică; RP, ZPP şi BPP

În ultimii douăzeci de ani cercetătorii din teoria complexităţii şi a algoritmilor au găsit aplicaţii surprinzătoare ale aleatorismului în rezolvarea de probleme. Aşa cum avem clasa de complexitate a problemelor care se pot rezolva în timp polinomial, avem şi clase de complexitate pentru probleme care se pot rezolva în timp polinomial dacă folosim aruncarea cu banul ca resursă.

Am văzut în episodul anterior al acestui foileton complex (adică ``foileton despre complexitate'') că despre foarte multe clase de complexitate nu se ştie dacă sunt identice sau doar incluse una într-alta. Astfel, nu se ştie daca P=NP, sau dacă P=PSPACE, etc. Din păcate la fel stau lucrurile şi în ceea ce priveşte aleatorismul: nu e clar dacă avînd aleatorism la-ndemînă putem calcula rapid lucruri pe care altfel nu le putem face decît foarte greu.

Vom discuta mai jos în text despre relaţia dintre aleatorism şi dificultatea problemelor. Pînă atunci să notăm că, la ora actuală, există o mulţime de probleme la care singurele soluţii eficiente cunoscute sunt probabilistice: nimeni nu cunoaşte soluţii deterministe de timp polinomial, dar există soluţii probabiliste de timp polinomial. Mai mult de atît: problemele de acest gen sunt extrem de importante în viaţa de zi cu zi; una dintre cele mai importante probleme pe care nu ştim s-o rezolvăm decît în mod aleator este criptarea.

Pînă atunci să aruncăm o privire asupra unor clase mari de probleme care se pot rezolva probabilistic. Ca şi în cazul maşinilor obişnuite, deterministe, teoreticienii consideră că problemele care se pot rezolva în timp polinomial în dimensiunea datelor de intrare sunt rezolvabile. De aceea lumea este interesata mai ales de clase de complexitate aleatoare pentru care timpul de găsire al soluţiei este de asemenea polinomial. De aceea trebuie să vă aşteptaţi (dacă aţi uitat cumva cum se cheamă această secţiune) ca numele acestora să se termine toate cu litera P, de la ``polinomial''.

Monte Carlo şi Las Vegas

Cum spuneam, există două clase de algoritmi aleatori, care pot greşi răspunsul, sau care pot depăşi timpul de execuţie. Ambele sunt numite după localităţi faimoase prin jocurile de noroc. Algoritmii care pot da rezultate greşite ocazional se numesc Monte-Carlo. Algoritmii care sunt întotdeauna corecţi în rezultat, dar pot depăşi un timp rezonabil de execuţie se numesc Las Vegas.

Trebuie să atragem atenţia că pentru cele două clase de algoritmi de obicei se măsoară lucruri diferite: pentru algoritmii Monte-Carlo masurăm, ca de obicei, cel mai mare timp de execuţie (worst case): cînd spunem că pentru date de intrare de mărime n un algoritm Monte-Carlo termină în timp O(f(n)), înseamnă că, indiferent de cum dăm cu banul, cel mai lung dintre timpii de execuţie pentru feluritele date de intrare de această mărime este mai mic de f(n).

Dimpotrivă, pentru algoritmii Las Vegas măsurăm ceea ce se numeşte timp mediu de execuţie pentru cazult cel mai rău (worst-case expected running time). Asta pentru că timpul de execuţie este o variabilă aleatoare; asta înseamnă că dacă dăm cu banul ceva, timpul e unul, dacă dam cu banul altceva, timpul e altul, chiar pentru aceleaşi date de intrare. Fiecare secvenţă de aruncări cu banul are o anumită probabilitate: secvenţa 00000 apare cu probabilitatea 2^-5, pentru că vrem să apară cinci zerouri consecutive, deci avem 1/2 * 1/2 * 1/2 * 1/2 * 1/2. Timpul mediu de execuţie este valoarea medie a variabilei aleatoare ``timp de execuţie'': $\Sigma_i p_i T(i, x)$ . În această formulă suma se face dupa toate şirurile aleatoare posibile i; p_i este probabilitatea ca şirul i să apară, iar T(i, x) este timpul de execuţie pentru date de intrare x cînd şirul aleator a fost i⁶

Iată un exemplu foarte simplu de algoritm Las Vegas de sortare: primim un şir de numere de lungime n, îl amestecăm în mod aleator, după care aplicăm QuickSort. Rezultatul va fi întotdeauna corect sortat, dar timpul de execuţie variază între n log n şi n². Din fericire, există foarte puţine şiruri aleatoare pentru care timpul de rulare este n², aşa încît timpul mediu de execuţie este n log n.

Aparent n-am făcut mare brînză, pentru că ştim deja că QuickSort în general sortează în timp n log n$. Dar acest lucru era valabil dacă datele de intrare se presupuneau egal probabile în orice ordine. Ori, în anumite circumstanţe, s-ar putea ca datele de intrare să apară mereu într-o ordine defavorabilă (de exemplu dacă datele de intrare vin de la un echipament de monitorizare a reţelei, s-ar putea ca fluctuătiile diurne regulate să facă ca datele să aibă mereu o formă nefavorabilă pentru un QuickSort simplu. Dar dacă noi amestecăm datele înainte de a le prelucra, în aşa fel încît orice şir de intrare să devină egal probabil, am distrus ne-uniformitatea din datele de intrare, permiţînd algoritmului să opereze în cazul său mediu!

BPP şi RP

Dacă ne restrîngem atenţia la probleme de decizie (adică la algoritmi care trebuie să dea mereu doar unul din răspunsurile ``da'' sau ``nu'')⁷, atunci putem distinge două clase de complexitate printre algoritmii Monte-Carlo.

Prima clasă de complexitate se numeşte RP, de la Randomized Polynomial time (timp aleator polinomial). Aceşti algoritmi pot face erori doar pentru unul din răspunsuri; mai exact, dacă răspunsul pentru nişte date de intrare trebuie să fie ``nu'', algoritmul răspunde 100% corect; dac'a r'aspunsul trebuie s'a fie ``da'', algoritmul ar putea cu probabilitate <1/4 să dea din greşeală răspunsul ``nu''. O problemă extrem de importantă practică este în clasa RP: testarea primalităţii unui număr. La ora actuală se cunosc numai algoritmi care vor recunoaşte întotdeauna corect un număr prim, dar care ar putea declara (eronat) că anumite numere compuse sunt de fapt prime, însă cu probabilitate mică (adică doar dacă sunt ghinioniste în aruncarea cu banul). Acesta este în sine un fapt foarte important, pentru că toţi algoritmii importanţi de criptografie cu cheie publică se bazează în construirea cheii pe generarea de numere prime, care la rîndul ei se bazează pe testarea primalităţii. Asta înseamnă de fapt că toată lumea care foloseşte RSA (o metodă foarte răspîndită de criptare; de exemplu atît Netscape cît şi Internet Explorer folosesc această metodă pentru anumite comunicaţii criptate prin Internet) are şansa să folosească o cheie care poate fi ``spartă'' uşor, pentru că nu e compusă din produsul a două numere prime! Din fericire, folosind tehnica amplificării, lumea reduce probabilitatea acestui eveniment la o valoare suficient de mică pentru a face algoritmul foarte folositor în practică.

A doua clasă de complexitate de algoritmi Monte-Carlo poate greşi cu probabilitate mică în oricare sens: dacă răspunsul e ``da'', atunci ar putea zice ``nu'' cu probabilitate <1/4, sau invers. Această clasă se numeşte BPP, de la Bounded-error Probabilistic Polynomial time. Amplificarea unui astfel de algoritm se face repetînd execuţia sa, şi luînd drept corect răspunsul care apare cel mai des.

Am văzut în numărul anterior al revistei că pentru fiecare clasă de complexitate putem vorbi de complementul său. Astfel avem clasele CoRP: clasa limbajelor pentru care dacă răspunsul este ``da'', atunci algoritmul îl găseşte întotdeauna, iar dacă răspunsul este ``nu'', algoritmul poate greşi cu probabilitate <1/4 (am inversat în definiţia lui RPpe ``da'' cu ``nu''). La fel se defineşte CoBPP, dar, din cauză că definiţia lui BPP este simetrică, CoBPP = BPP. Pe de altă parte, RP $\not=$ CoRP.

Mai mult de atît, intersecţia RP $\cap$ CoRP = ZPP se numeşte Zero-error Probabilistic Polynomial time. Se poate uşor arăta că de fapt ZPP este chiar clasa algoritmilor Las Vegas cu timp mediu polinomial.

Se cunosc anumite relaţii între aceste clase de complexitate şi cele clasice, dar, ca de obicei, nu se ştie dacă relaţiile de incluziune sunt sau nu stricte: ${\bf P}\subseteq {\bf RP}\subseteq {\bf NP}$ , şi ${\bf RP}\subseteq {\bf BPP}$ .

Nota: revista PC Report şi-a exprimat dezinteresul pentru articole pe teme atît de teoretice, ca atare acest articol este neterminat.

Teoria complexităţii

Note