Mihai Budiu -- mihaib+@cs.cmu.edu
http://www.cs.cmu.edu/~mihaib/
18 august 1999
Articolul de faţă atacă o problemă foarte importantă în informatică, din mai multe puncte de vedere (din mai multe puncte de vedere este atît importanţa cît şi atacul meu). Problema aceasta este extrem de importantă pentru practicieni, pentru că apare în extrem de multe contexte în viaţa ``reală'', sau foarte multe alte probleme reale se pot reduce la ea (definim precis noţiunea de ``reducere'' undeva mai jos).
Problema este însă şi mai importantă pentru teoreticieni, din mai multe motive. În primul rînd, nu se cunoaşte nici o soluţie eficace pentru această problemă, în cazul ei cel mai general. Toate metodele de calcul sunt extrem de costisitoare, făcînd imposibilă rezolvarea unor instanţe de dimensiuni mari. Pe de altă parte, complexitatea algoritmilor cunoscuţi îndepărtează speranţa că vreodată vom avea suficiente resurse pentru a rezolva instanţe mari ale acestei probleme; chiar creşteri ale performanţei calculatoarelor de milioane de ori ar permite creşterea numărului de variabile din cu doar cîteva zeci de unităţi (iar problemele practice pot avea zeci de mii de variabile).
În fine, mult mai interesant, problema aceasta este într-un anume sens ``cea mai grea problemă din clasa ei de probleme''. Sunt extrem de multe alte probleme practice care sunt echivalente, sau mai uşoare, decît această problemă. Teoreticienii au demonstrat că dacă, putem soluţiona problema de faţă în mod eficient, atunci toate celelalte probleme echivalente sau mai uşoare se pot rezolva extrem de eficient, în mod imediat. O consecinţă surprinzătoare a acestui fapt ar fi că criptografia ar fi inexistentă, pentru că orice metodă de criptare ar putea fi spartă în mod eficient.
În fine, problema aceasta are implicaţii interesante pentru filozofie, pentru că, într-un anume sens, ne ajută să măsurăm diferenţa dintre geniu şi normalitate, dintre creativitate şi simpla înţelegere pasivă. Existenţa unei soluţii eficace pentru această problemă ar avea de pildă consecinţa surprinzătoare că pentru fiecare teoremă din matematică există o metodă foarte eficace de a o demonstra cu calculatorul; asta ar transforma întreaga muncă de creaţie a matematicienilor într-o treabă de rutină, pe care o poate face o maşină de calcul.
Problema aceasta este piatra de temelie a unei ramuri a informaticii numită ``teoria complexităţii'', căreia intenţionez să-i consacru în viitor un întreg articol. Existenţa unei soluţii eficace pentru problema din acest articol este considerată aproape unanim cea mai importantă problemă nerezolvată din ştiinţa calculatoarelor.
Şi acum, că v-am trezit curiozitatea, să purcedem să vedem cum se înlănţuie toate aceste fapte.
Trebuie dintru început să facem distincţie dintre o clasă de probleme şi instanţele problemei. O clasă de probleme este o colecţie de instanţe înrudite.
În general, un program pentru calculator (un algoritm) rezolvă orice instanţă dintr-o clasă. De exemplu, în procesorul Pentium se află o unitate aritmetică folosită pentru a efectua adunări. Această unitate aritmetică rezolvă următoarea clasă de probleme: ``care este rezultatul adunării a două numere mai scurte de 32 de biţi?'' O instanţă a acestei probleme este ``cît face 3+7?''. Observaţi că unitatea aritmetică poate rezolva orice instanţă. Nu ar fi foarte folositor dacă ar putea rezolva numai întrebarea ``cît e 3+7?''.
În general nu avem nevoie să rezolvăm chiar toate instanţele, dar pentru că e prea complicat să construim maşini speciale pentru fiecare instanţă (şi nu prea practic), facem maşini care rezolvă clase întregi de probleme (adică pot rezolva orice instanţă).
Observaţi că clasa de probleme: ``fiind dat un număr n, care este rezultatul adunării a oricare două numere de n biţi'' este o clasă mai largă decît cea rezolvată de Pentium, pentru care n=32. Putem scrie un program care să calculeze în principiu suma oricăror două numere, oricît de lungi ar fi ele. Cum arată programul, am învăţat cu toţii în şcoala primară, folosind tabla adunării. Folosind această tablă putem aduna numere oricît de lungi (dacă nu obosim).
În general, teoreticienii studiază astfel de clase de probleme, în care ``dimensiunea'' datelor de intrare nu este limitată apriori de nici o valoare. Ei sunt interesaţi să afle dacă putem scrie programe care să funcţioneze şi atunci cînd nu se cunoaşte această dimensiune dinainte.
Este de altfel o idee foarte bună ca algoritmii pe care îi implementaţi să fie proiectaţi în aşa fel încît să poată trata probleme oricît de mari. Orice limitare arbitrară impusă datelor de intrare se poate dovedi extrem de neplăcută mai tîrziu; în definitiv din asta a şi provenit celebrul bug Y2K: programatorii nu au permis programelor să manipuleze decît date într-un interval de 100 de ani, ceea ce are consecinţe economice uriaşe la ora actuală (companiile cheltuiesc acum zeci de miliarde de dolari să descopere şi corecteze astfel de imperfecţiuni).
Definim un algoritm astfel: o procedură de calcul efectiv, care rezolvă orice instanţă dintr-o anumită clasă de probleme. Nu uitaţi că întotdeauna algoritmul este legat de clasă; pentru clase diferite putem avea algoritmi diferiţi, chiar dacă clasele sunt înrudite. De exemplu, pentru clasa de probleme: ``care este suma a două numere mai mici ca 100?'' putem face un algoritm foarte simplu, care pre-calculează toate sumele posibile, după care caută rezultatul într-o tabelă bidimensională de 100*100 de numere. Desigur, algoritmul risipeşte o mulţime de spaţiu, dar răspunde practic instantaneu. Este clar că acest algoritm nu se poate generaliza pentru a face orice adunare, în care lungimea numerelor nu este limitată dinainte.
Voi introduce acum clasa de probleme care constituie subiectul principal al acestui articol. Pentru început însă voi trece în revistă rapid funcţiile boolene, pentru că problema noastră este legată de ele.
Georges Boole a trăit între 1815 şi 1864. În istoria ştiinţei el este cunoscut mai ales prin rezultatele sale matematice, ca creator al algebrei boolene (numită, evident, în cinstea sa). Aceasta este o algebră extrem de simplă, care operează cu numai două valori, 0 şi 1.
Dar Boole este extrem de important şi în istoria filozofiei, pentru că algebra lui a fost creată în încercarea de a formaliza în limbajul matematicii logica aristotelică clasică. Georges Boole este considerat de unii părintele logicii matematice. Boole era interesat să reformuleze legile gîndirii umane în termeni matematici.
Algebra booleană operează cu valori de adevăr, din care avem numai două: adevărat şi fals. Orice variabilă are la un moment dat exact una dintre aceste două valori. 0 este folosit pentru a denota falsul, iar 1 pentru adevărat.
Boole a introdus anumite operaţii pentru manipularea valorilor
boolene: operaţiile de ``şi'' logic (![]() ), ``sau'' logic
(
), ``sau'' logic
(![]() ) şi negaţie logică (
) şi negaţie logică (![]() ). (Putem introduce şi alte
operaţii, dar acestea sunt cele mai importante.)
). (Putem introduce şi alte
operaţii, dar acestea sunt cele mai importante.)
Putem combina valori boolene folosind aceste operaţii, şi putem calcula valoarea de adevăr a unor propoziţii complicate într-un mod foarte limpede.
De exemplu, dacă avem două propoziţii logice oarecare, a şi b,
putem vorbi de propoziţia ![]() (a şi b), care este
adevărată numai cînd ambele propoziţii sunt adevărate. Modul de
operare al lui
(a şi b), care este
adevărată numai cînd ambele propoziţii sunt adevărate. Modul de
operare al lui ![]() poate astfel fi descris în acelaşi fel ca cel
al operaţiilor aritmetice obişnuite, cu o tabelă (cum e tabla
adunării), aşa cum arată figura 1.
poate astfel fi descris în acelaşi fel ca cel
al operaţiilor aritmetice obişnuite, cu o tabelă (cum e tabla
adunării), aşa cum arată figura 1.
De exemplu, dacă avem propoziţiile ``Afară plouă'' şi ``E ora 7'', propoziţia formată din conjuncţia acestora (adică legarea celor două cu ``şi'') este ``E ora 7 şi afară plouă''. În mod evident, această propoziţie este adevărată doar dacă ambele enunţuri mai simple sunt adevărate, justificînd tabela operaţiei ``şi''.
| ||||||||||||||||||||||||||||||||||||||
O altă operaţie logică este cea numită ``sau'': rezultatul este adevărat dacă măcar una dintre valorile combinate este adevărată1.
În fine, avem operaţia de negare (``nu''), care inversează valoarea de adevăr a unei propoziţii2.
Operaţiile boolene sunt asociative şi comutative. Putem astfel scrie prescurtat formule boolene complicate, de genul:
Algebra booleană este enorm de importantă în calculatoare; componentele electronice de bază din care este construit un calculator sunt ``porţile logice'', care implementează exact aceste operaţii, manipulînd curenţi electrici pentru a reprezenta valori boolene (anumite potenţiale fiind alese în mod convenţional pentru a reprezenta valorile 0 şi 1). Altfel de dispozitive sunt foarte uşor de construit din tranzistoare, care apoi se pot construi la o scara minusculă, înghesuind milioane pe o pilulă de siliciu.
Dacă ni se dă o formulă booleană şi o serie de valori pentru variabilele care o compun, putem scrie un algoritm foarte simplu şi eficient care evaluează formula. Acesta este chiar algoritmul bine-cunoscut folosit pentru evaluarea expresiilor aritmetice, cu diferenţa că operează doar cu valori boolene.
Acum suntem în măsură să formulăm problema care ne interesează, numită problema satisfiabilităţii, (satisfiability), pe scurt SAT: ``fiind dată o formulă booleană, există o atribuire a variabilelor care o compun care face formula adevărată?''.
Îmi aduc aminte de un banc: ``Cică un inginer şi un matematician dimineaţa îşi făceau ceaiul, aplicînd următorul algoritm: <<Ia ibricul, umple-l cu apa, pune-l pe foc, fierbe apa, pune plicul, toarnă în cană>>. Dar într-o zi, nevestele lor le lasă ibricul cu apă înauntru. Ce fac cei doi? Ei bine, inginerul aplică algoritmul de la al doilea pas: pune-l pe foc, fierbe apa, pune plicul, toarnă în cană. În schimb matematicianul varsă apa în chiuvetă şi reduce problema la cea precedentă.''
Bancul este amuzant (găsesc eu), dar conceptul de reducere este cu adevărat util. Cel puţin în calculatoare, are extrem de multe aplicaţii. Aici ne vom uita la doar una dintre ele.
Adesea putem abstractiza o problemă şi o putem enunţa într-un alt fel; de fapt, chiar pentru a rezolva probleme practice, în general le abstractizăm în termeni matematici, după care aplicăm tehnici din domeniul matematicii.
Figura 1 ilustrează noţiunea de reducere pentru probleme în teoria complexităţii.
Ei bine, se întîmplă că problema SAT este o problemă extrem de expresivă; putem enunţa o mulţime de alte probleme sub forma SAT.
 |
Voi ilustra aici aici o reducere foarte simplă, între o problemă numită ``colorarea unei hărţi cu două culori'' şi SAT.
Să presupunem că avem o hartă pe care vrem să o colorăm în aşa fel încît oricare două ţări alăturate să aibă culori diferite.
Asociem fiecărei ţări o variabilă booleană. Apoi pentru fiecare
vecinătate dintre două ţări creăm o clauză3:
dacă ţara A este vecină cu ţara B, atunci creăm clauza
![]() . Vom folosi valoarea 0 pentru a denota o culoare, şi
valoarea 1 pentru cealaltă. Formula de mai sus spune că ţările
A şi B nu pot avea aceeaşi culoare simultan, pentru că dacă
variabilele A şi B au aceeaşi valoare, atunci clauza de mai sus
va fi falsă.
. Vom folosi valoarea 0 pentru a denota o culoare, şi
valoarea 1 pentru cealaltă. Formula de mai sus spune că ţările
A şi B nu pot avea aceeaşi culoare simultan, pentru că dacă
variabilele A şi B au aceeaşi valoare, atunci clauza de mai sus
va fi falsă.
Formula booleană pe care vrem s-o satisfacem este conjuncţia tuturor acestor clauze.
Dacă formula este satisfiabilă, culorile ţărilor corespund valorilor variabilelor boolene respective. Dacă formula nu este satisfiabilă, atunci nici problema originală nu are soluţie.
Deci dacă rezolvăm problema satisfiabilităţii, atunci putem rezolva şi problema colorării unei hărţi cu două culori. Aceasta este deci o reducere de la una la cealaltă.
Iată nişte exemple de probleme cu însemnătate foarte mare pentru activitatea umană, care se pot reduce la SAT cu uşurinţă:
Şi lista ar putea continua cu multe alte probleme.
Vedeţi, faptul că aceste probleme sunt toate reductibile la SAT ne spune două lucruri:
Din păcate, vom vedea puţin mai jos că speranţele noastre de a rezolva aceste probleme sunt foarte reduse.
Aparent SAT este o problemă banală, şi algoritmul pentru a o rezolva este foarte simplu:
Într-adevăr, algoritmul de mai sus este corect; dacă există o distribuţie de valori pentru care formula este adevărată, o va găsi. Dacă nu este nici una, atunci va da corect răspunsul ``nu'' odată ce a examinat toate posibilităţile. Acest algoritm este corect, dar nu este şi eficient. Dacă nu credeţi acest lucru, atunci încercaţi să executaţi algoritmul pentru o formulă cu 64 de variabile.
Din modul în care am expus algoritmul deficienţa este vizibilă: dacă avem k variabile, atunci trebuie să incrementăm de la 0 la valoarea maximă un contor cu k cifre. Ori acest contor trebuie incrementat de 2k ori. Pentru 64 de pildă putem aproxima 210 = 103, deci 264 = 1018 * 16 = 1019. Dacă un calculator execută o instrucţiune la o nanosecundă (adică are un ceas de un gigahertz), îi vor trebui 1019/109 = 1010 secunde pentru a efectua doar incrementarea. Un an are cam 3 * 107 secunde, deci durata calculului ar fi de circa 30 de ani!
Dacă asta vi se pare o bagatelă, atunci încercaţi să rezolvaţi o problemă doar puţin mai mare, să zicem cu 70 de variabile (10% mai mare). Ei bine, asta o să dureze de 64 de ori mai mult, adică 1800 de ani!
Desigur, timpul acesta de rulare va fi petrecut doar dacă formula pe care o verificaţi nu este satisfiabilă, pentru că atunci contorul trebuie să treacă prin toate valorile.
Teoria complexităţii măsoară timpul de execuţie al unui algoritm ca o funcţie de cantitatea de date oferite spre prelucrare. Dacă măsurăm formula SAT de la intrare după numărul de variabile n, atunci algoritmul de mai sus se poate executa pentru o durată proporţională cu 2n, pentru anumite formule.
Cea mai ades folosită metodă de măsurare a complexităţii unui
algoritm consideră cel mai defavorabil caz posibil. De exemplu,
printre formulele SAT de lungime 2 exista multe care se pot rezolva
imediat, pentru că din prima încercare putem spune că formula este
satisfiabilă (de exemplu formula
![]() ). Dar există cel
puţin o formulă de lungime 2 pentru care algoritmul trebuie să
facă toate cele 4 încercări posibile. Din cauza aceasta, spunem
că complexitatea algoritmului de mai sus este de ordinul 2n, unde
în mod implicit cu n se notează dimensiunea datelor de
intrare5.
). Dar există cel
puţin o formulă de lungime 2 pentru care algoritmul trebuie să
facă toate cele 4 încercări posibile. Din cauza aceasta, spunem
că complexitatea algoritmului de mai sus este de ordinul 2n, unde
în mod implicit cu n se notează dimensiunea datelor de
intrare5.
Vedeţi, am spus că complexitatea este ``proporţională cu'', şi nu ``exact'' 2n. Această caracterizare este destul de precisă, însă, pentru că, indiferent care este coeficientul de proporţionalitate, (care de altfel depinde de viteza procesorului şi de alţi factori), modul în care acest algoritm se comportă pentru probleme foarte mari este acelaşi: este complet ne-practic.
Teoria complexităţii consideră că orice clasă de probleme pentru care complexitatea unui algoritm este proporţională cu un o funcţie polinomială este eficace; prin contrast, atunci cînd complexitatea este proporţională cu o funcţie exponenţială (ca mai sus), problema este considerată nerezolvabilă.
Pentru ilustraţie, algoritmii cei mai buni care sortează în ordine crescătoare un şir de n numere, au un timp de execuţie proporţional cu n log n, care este o funcţie mai mică decît polinomul n2 (pentru că funcţia logaritmică creşte mai încet decît orice polinom). Problema sortării are deci o soluţie eficace.
Deci algoritmul de mai sus pentru SAT nu este prea eficace, cel puţin dacă avem intenţia de a rezolva probleme foarte mari. Înseamnă asta că problema este practic nerezolvabilă?
Desigur, nu. Dacă am face această afirmaţie, ar fi ca şi cum am zice că nu putem ajunge la Ploieşti de la Bucureşti decît după 10 zile, pentru că aşa am ajuns la un moment dat mergînd prin Japonia.
Faptul că avem un algoritm lent pentru o problemă nu înseamnă că problema este grea. Poate există un alt algoritm, care rezolvă problema mult mai bine!
Algoritmul de mai sus nu exploatează în nici un fel înfăţişarea
formulei. De pildă, dacă formula conţine următoarele două
clauze: a şi ![]() , putem spune imediat că formula nu este
satisfiabilă, pentru că, orice valoare ar avea a, şi independent
de valorile tuturor celorlalte variabile, rezultatul formulei va fi
tot 0.
, putem spune imediat că formula nu este
satisfiabilă, pentru că, orice valoare ar avea a, şi independent
de valorile tuturor celorlalte variabile, rezultatul formulei va fi
tot 0.
E adevărat că putem scrie tot felul de algoritmi mai inteligenţi, dar pînă la ora actuală nimeni nu a reuşit să găsească un algoritm eficace pentru SAT, care, pentru orice instanţă a problemei să ofere răspunsul într-un timp mai scurt decît cel exponenţial.
Mai mult decît atît, sunt dovezi foarte convingătoare (dar nu şi o demonstraţie exactă) că SAT nu admite o soluţie eficientă. Poate să pară intuitiv clar că SAT are nevoie de foarte mult timp, dar nu există nici demonstraţia inversă, cum că SAT nu poate fi rezolvată rapid.
``Ei, şi ce?'' o sa întrebaţi. Cine are nevoie de SAT? Din păcate, foarte multă lume.
Am văzut mai sus că foarte multe probleme se pot reduce la SAT. Asta înseamnă că dacă am găsi o soluţie eficientă pentru SAT, am putea rezolva eficace şi aceste probleme practice.
Toate problemele de mai sus au o trăsătură foarte interesantă: nu ştie nimeni cum să le găsească o soluţie, dar de îndată ce cineva ne-ar da un răspuns pentru o instanţă, am putea verifica foarte repede dacă acela este răspunsul corect.
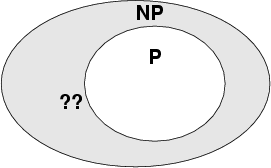
Teoria complexităţii defineşte astfel o mulţime de probleme numită NP (de la Nedeterminist-Polinomial, o denumire tradiţională, care are o justificare despre care nu vom discuta acum): clasa NP este compusă din toate problemele pentru care putem verifica foarte eficient dacă un anumit răspuns este o soluţie corectă (eficient înseamnă, din nou, că verificarea durează un timp polinomial în mărimea problemei pe care o avem de rezolvat). SAT şi toate problemele de mai sus fac parte din NP.
Se defineşte de asemenea clasa tuturor problemelor pentru care ştim să calculăm răspunsul exact într-un timp scurt, polinomial în lungimea datelor de la intrare. Această clasă este denumită simplu, P6.
De exemplu, problema circuitului hamiltonian este în clasa NP pentru că, dacă cineva ne dă o listă de oraşe putem verifica foarte rapid dacă această listă formează sau nu un circuit hamiltonian. Pentru a face asta verificăm că fiecare oraş apare o singură dată în listă, că toate oraşele de pe hartă apar, şi că între fiecare două oraşe consecutive din listă chiar există un drum direct. Prin definiţie deci, această problemă este în clasa NP. Nimeni nu cunoaşte însă un algoritm eficient pentru a decide dacă un ciclu hamiltonian există, deci nu ştim dacă această problemă este în clasa P.
Ei bine, toate problemele din P fac parte şi din clasa NP. Asta pentru că dacă ni se dă răspunsul la o problemă din P, pentru a verifica dacă este corect nu facem decît să executăm algoritmul eficace pentru a găsi soluţia, şi să comparăm soluţia oferită cu cea calculată. Figura 2 rezumă starea cunoştinţelor noastre la ora actuală.
 |
Ar fi minunat dacă am putea găsi soluţii eficiente pentru toate problemele care sunt în NP, mai ales că multe dintre ele sunt probleme de o mare importanţă economică şi practică.
În 1971 Stephen Cook a demonstrat7 o teoremă celebră, care arată că orice problemă din NP se reduce la SAT. Am văzut mai sus că anumite probleme sunt reductibile la SAT; Cook a arătat printr-un argument ingenios că orice altă problemă am avea (chiar cele ne-formulate încă), dacă putem verifica soluţiile acelei probleme într-un mod eficace (deci dacă problema este în clasa NP), atunci problema este reductibilă la SAT.
Asta înseamnă că, dacă ni se dă o instanţă a unei probleme oarecare din NP, putem construi în mod automat o instanţă a unei probleme SAT. Construcţia aceasta însăşi se poate face într-un mod foarte eficace (adică putem face construcţia în timp polinomial). Construcţia garantează faptul că orice soluţie a problemei SAT construite corespunde unei soluţii a problemei reale. Astfel, putem acum rezolva problema SAT în locul problemei originale, şi apoi putem ``decodifica'' răspunsul.
Ce ne spune teorema lui Cook?
Ne spune în primul rînd că SAT este problema ``cea mai importantă'' din clasa NP, pentru că, dacă o putem rezolva eficient, putem rezolva toate celelalte probleme din NP. De fiecare dată cînd găsim o problemă în NP, nu avem decît să facem o reducere a problemei la SAT, să rezolvăm problema SAT, şi apoi să convertim înapoi răspunsul în termenii problemei originare. Acest lucru este întotdeauna posibil.
Pe de altă parte, dificultatea găsirii răspunsului la problema originară este clar mai mică decît dificultatea rezolvării problemei SAT (avînd un răspuns la SAT obţinem un răspuns la problema originară, dar nu neapărat şi invers).
Putem deci considera în acest sens SAT ca fiind cea mai grea problemă din NP. Din aceste motive, SAT este numită o problemă NP-completă. Acesta este un rezultat deosebit de important, pentru că ne spune că mai curînd vom găsi algoritmi eficienţi pentru oricare altă problemă din NP decît pentru SAT. Pentru că foarte multe din celelalte probleme sunt încă nerezolvate, nu sunt prea multe şanse să rezolvăm SAT.
Deci SAT este cea mai grea problemă. Partea proastă este că în decursul vremii oamenii au reuşit să arate că există o sumedenie de alte probleme din NP care... sunt mai grele ca SAT!
Pentru a demonstra că o problemă este ``mai grea'' ca SAT nu trebuie decît să facem lucrul invers: să reducem pe SAT la acea problemă. Asta ne permite să codificăm orice instanţă SAT ca pe o instanţă a acelei probleme, şi ne permite să rezolvăm SAT punînd întrebări despre instanţe ale celeilalte probleme.
Dacă o problemă este mai grea decît SAT, din moment ce SAT este deja cea mai grea problemă, ajungem la concluzia că acea problemă este la fel de grea ca SAT; dificultatea ambelor probleme este aceeaşi. Cele două probleme sunt practic echivalente.
Demonstrarea că o problemă este mai grea decît SAT nu este în general o treabă uşoară. Cu toate acestea, toate problemele enunţate în lista de mai sus (circuitul hamiltonian, problema planificării, problema rucsacului, etc.), repet, probleme de o deosebită importanţă practică, sunt demonstrate a fi mai grele decît SAT.
Toate aceste probleme sunt deci la rîndul lor NP-complete!
Închei aici prima parte a prezentării mele despre SAT; acesta este partea cea mai tehnică, deşi evită orice demonstraţie. În realitate teorema lui Cook nu este prea complicată, şi în afară de noţiunile expuse în acest text nu mai este nevoie de mare lucru pentru a o înţelege. Cititorul interesat este trimis de pildă la cartea lui Papadimitriou ``Computational Complexity'', sau la cartea lui Weinker & Davis ``Computability, Complexity and Languages''.
În partea a doua a acestui text (în numărul viitor) voi discuta despre alte implicaţii ale problemei SAT, despre interpretarea filozofică a clasei NP, despre soluţiile practice euristice care s-au găsit pentru a rezolva unele dintre instanţele acestei probleme, şi despre nişte proprietăţi statistice interesante ale densităţii soluţiilor problemei.
Mesajul cel mai important al acestui text se află însă în partea de faţă. Am văzut în acest text că între anumite probleme computaţionale putem face reduceri, astfel încît să transformăm soluţiile uneia în soluţiile celeilalte. Am văzut de asemenea că există o clasă foarte interesantă de probleme (numită NP) pentru care ştim să verificăm eficient dacă ceva este o soluţie, dar nu avem nici o idee despre cum să găsim o soluţie. Am văzut şi că SAT este o astfel de problemă, şi că orice altă problemă din NP se poate reduce la SAT, făcînd din SAT o problemă NP-completă.
Dacă cel puţin un cititor găseşte aceste fapte demne de interes, sunt satisfăcut; mai satisfăcut decît probabil SAT va fi vreodată.
În numărul anterior din PC Report am consacrat un articol unei probleme pe care am numit-o cu emfază ``cea mai importantă problemă nerezolvată din informatică''. Textul de faţă este o continuare; cititorii care nu posedă primul episod sunt invitaţi să obţină o copie a textului din pagina mea de web.
Problema de care vorbim se numeşte problema ``satisfiabilităţii'', notată pe scurt cu SAT. Un enunţ foarte intuitiv, pentru cei cu oarecare noţiuni despre arhitectura calculatoarelor, este următorul: ``Fie un circuit digital combinaţional (adică fără cicluri), construit din porţi logice ``sau'', ``şi'', ``nu'', care are o singură valoare la ieşire. Există o combinaţie de valori la intrarea circuitului care cauzează ieşirea circuitului să fie 1?''.
În textul anterior am formulat această întrebare pentru o formulă booleană (o formulă care operează cu operatorii algebrei boolene, introdusă de George Boole); cele două formulări sunt echivalente, deoarece porţile logice ale unui circuit combinaţional corespund operaţiilor boolene, în aşa fel încît fiecare formulă corespunde unui circuit şi invers.
De fapt găsirea unui algoritm care să ofere răspunsul corect la această problemă nu este un lucru prea greu; neplăcerea constă în faptul că nu se cunoaşte nici un algoritm eficace, care să fie capabil să rezolve probleme mari într-un timp scurt. Toţi algoritmii cunoscuţi, inclusiv cei prezentaţi ceva mai jos, au trăsătura indezirabilă că există instanţe ale problemei pentru care timpul de execuţie este exponenţial în dimensiunea problemei. Asta înseamnă că, dacă adăugăm o singură variabilă în plus, timpul necesar rezolvării se dublează. Este uşor de văzut că acest ritm de creştere este covîrşitor, şi că întreaga capacitate de calcul a omenirii nu este suficientă pentru a trata probleme de dimensiuni nu prea mari (zeci de mii de variabile).
Existenţa unei soluţii eficace pentru problema satisfiabilităţii nu este considerată cea mai importantă din întreaga informatică doar de către nişte teoreticieni amatori de curiozităţi. Importanţa practică a acestei probleme este enormă: foarte foarte multe probleme practice sunt echivalente ca dificultate cu problema satisfiabilităţii. Michael Garey şi David Johnson au alcătuit în 1979 o culegere de probleme, toate echivalente cu SAT: ``Computers and Intractability: A Guide to the Theory of NP-Completeness'', publicată de editura W. H. Freeman. Între timp lista aceasta a crescut mult; la ora aceasta cuprinde cîteva mii de exemple.
Toate aceste probleme au o trăsătură foarte interesantă în comun: pentru nici una nu se cunoaşte o soluţie eficientă (adică un algoritm eficient care să rezolve toate instanţele acestor probleme), dar nici nu există argumente că astfel de soluţii nu ar exista. Dacă măcar am şti că nu există soluţii eficiente, poate am fi mai împăcaţi, chit că aflarea soluţiei ar putea avea importanţă economică de miliarde de dolari. Dar nu ştim că nu putem, aşa că suntem nervoşi.
Mai mult decît atît: dacă noi căutăm soluţia şi cineva vine şi zice: ``ştiu răspunsul: formula ta nu este satisfiabilă''. Noi îl putem provoca: ``dovedeşte''. Ei bine, atunci acel cineva poate produce o dovadă simplă că are dreptate şi că ştie într-adevăr soluţia. Cu alte cuvinte, pentru aceste probleme există dovezi simple şi uşor de verificat că ceva este o soluţie8.
Există o denumire specială pentru problemele pentru care putem verifica imediat dacă o pretinsă soluţie este corectă: toate aceste probleme formează aşa numita clasă NP, de la nedeterminist-polinomial. SAT este o astfel de problemă, pentru că dacă cineva ne arată intrările unui circuit putem imediat vedea dacă circuitul va obţine un ``1'' la ieşire.
În prima parte a acestui articol menţionam că în 1971 Cook a demonstrat că SAT este cea mai grea problemă din clasa NP, în sensul că orice altă problemă din NP se reduce la SAT. Din cauza asta SAT este numită o problemă NP-completă, la fel ca toate celelalte probleme echivalente prezentate în culegerea lui Garey şi Johnson.
Prin contrast, clasa tuturor problemelor pe care le putem rezolva eficient (care sunt definite ca probleme pentru care cunoaştem algoritmi al căror timp de rulare este proporţional cu o funcţie polinomială în dimensiunea problemei) se numeşte P.
NP nu este nici pe departe clasa problemelor celor mai dificile pe care le cunoaştem; există clase de complexitate mult mai grele, ca de pildă EXP, clasa problemelor pentru care cu siguranţă nu există soluţii ne-exponenţiale ca timp. Există chiar clasa problemelor nedecidabile, pentru care nu există... nici un fel de soluţie9!
De fapt teoria complexităţii demonstrează existenţa a tot felul de ierarhii de clase de complexitate şi studiază relaţiile dintre feluritele clase. Adesea relaţiile sunt de incluziune, aşa cum avem între P şi NP: orice problemă P este şi una NP; uneori însă relaţiile sunt mai bizare, sau sunt condiţionate de alte relaţii (ceva de genul: dacă clasa A e diferită de clasa B, atunci clasa D e tot una cu clasa C). Teoria complexităţii clasifică problemele în funcţie nu neapărat de timpul necesar soluţionării, ci şi în funcţie de alte resurse necesare, cum ar fi: cantitate de memorie necesară (numită şi spaţiu), număr de biţi aleatori, porţi logice, ``adîncimea'' unui circuit care rezolvă problema, etc.
Lumea face atît de mult tam-tam vis-a-vis de NP nu numai pentru că există în NP multe probleme practice importante (căci şi celelalte clase de complexitate conţin probleme practice importante), ci şi pentru că pentru problemele din NP există speranţa că ar putea fi rezolvate rapid, dar nimeni nu ştie cum. Dacă am şti că nu se poate, am fi probabil mai relaxaţi, dar aşa e ca şi cum soluţia ne scapă printre degete.
În acest paragraf vom discuta o trăsătură foarte interesantă a lui SAT. SAT, aşa cum este ea formulată, este o ``problemă de decizie''; acest nume tehnic înseamnă doar că răspunsul trebuie să fie doar ``DA'' sau ``NU'': dacă ni se dă un circuit, trebuie să spunem doar dacă circuitul este satisfiabil sau nu, dar nu şi cum este satisfiabil.
Aparent capacitatea de a rezolva o problemă de decizie nu e prea utilă: dacă un profesor la şcoală are voie să pună numai întrebări la care studentul să răspundă numai cu ``DA'' sau ``NU'', nu pare să poată verifica prea bine cunoştinţele studenţilor în acest fel (în definitiv dacă aceştia dau cu banul au şansa de a răspunde 50% corect, deci s'a ia not'a de trecere fără nici un efort).
În realitate însă această limitare la probleme de decizie nu este o constrîngere prea severă. Folosind un procedeu numit auto-reducere putem transforma mai multe răspunsuri DA-NU într-o soluţie completă (adică putem afla şi cum circuitul poate fi făcut satisfiabil, pentru care intrări). Iată cum:
Să presupunem că avem la dispoziţie un algoritm care rezolvă rapid şi corect SAT, în sensul că răspunde întotdeauna ``DA'' cînd i se dă o formulă SAT care poate genera ``1'' şi ``NU'' cînd pentru toate intrările posibile ale circuitului rezultatul este ``0''.
Vrem să găsim o serie de intrări pentru care rezultatul este ``1'', dacă acestea există.
Putem atunci proceda în acest fel :
După atîţia paşi cîte variabile avem, obţinem pentru fiecare variabilă o valoare.
(Putem apoi verifica dacă algoritmul nu a minţit, testînd valoarea formulei cu valorile obţinute. Acelaşi truc îl poate face şi profesorul pentru a testa un student numai cu răspunsuri ``DA'' şi ``NU'': întreabă în felul următor: ``este prima literă din capitala Braziliei A'', apoi, dacă răspunsul studentului este ``da'', întreabă de a doua literă, altfel încearcă B pentru prima, etc. Deşi metoda este incomodă, este pe deplin în concordanţă cu regulile jocului, şi aproape infailibilă: profesorul obţine cîte un bit de la student prin fiecare întrebare. Dacă studentul ştie răspunsul, profesorul trebuie să obţină toţi biţii corecţi, şi nu numai unul.)
Metoda auto-reducerii este extrem de puternică: ne permite să folosim un potenţial algoritm pentru a rezolva SAT pentru a rezolva o sumedenie de alte probleme, aparent mult mai complicate (de exemplu, chiar problema de a găsi valorile care fac o formulă satisfiabilă).
Suntem înclinaţi să afirmăm că există o diferenţă substanţială între (1) a înţelege ceva şi (2) a crea ceva nou. Aceste două feluri de activitate sunt net diferite: spectatorul unei opere de artă apreciază rezultatul, dar efortul artistului pentru a crea acea operă pare mult mai impresionant. Putem spune că aprecierea este un algoritm de clasă P, dar creaţia este unul de clasă NP: putem aprecia rezultatul, dar nu ştim cum să-l producem.
Dacă vă deranjează excursul într-un domeniu care este rezervat subiectivităţii totale (arta), atunci putem face exact aceeaşi analogie în matematică: între (1) a demonstra o teoremă şi (2) a citi o demonstraţie făcută de altcineva şi a ne convinge de corectitudinea ei, pare să fie din nou o diferenţă de natură. Actul (1), al demonstratorului este un act creativ, de căutare într-o enormă masă de posibilităţi, pe cînd actul (2), al discipolului, care reciteşte demonstraţia, este relativ simplu, constînd în a verifica faptul că fiecare pas logic făcut în demonstraţie respectă regulile de inferenţă ale logicii.
Din nou avem aceeaşi antiteză, între actul de a genera (care poate fi asimilat cu clasa NP) şi actul de a verifica (care poate fi asimilat cu clasa P)10.
Cum spuneam, nu există o demonstraţie riguroasă că P ![]() NP,
dar nici una că P=NP. Suntem supuşi unei tensiuni dureroase:
NP,
dar nici una că P=NP. Suntem supuşi unei tensiuni dureroase:
Dacă P=NP, am avea şi alte consecinţe extrem de importante, în oarecare măsură devastatoare:
Pentru orice teoremă din matematică am putea scrie un program care să găsească o demonstraţie într-un timp nu mult mai mare decît lungimea celei mai scurte demonstraţie posibile (ar exista un polinom P(x) astfel încît, dacă cea mai scurtă demonstraţie posibilă este de lungime x, algoritmul am găsi una în timp cel mult P(x).).
Un astfel de algoritm ar folosi tehnica auto-reducerii pentru a deriva o demonstraţie corectă (ceva de genul: există o demonstraţie care începe cu litera ``A''? etc.)
Importanţa acestei tehnici pentru demonstrarea automată a teoremelor din matematică a fost observată de către logicianul Kurt Gödel înca din 1956, într-o scrisoare adresată marelui matematician John von Neumann, cu mult înainte ca teoria NP-complexităţii să existe (şi cu mult înainte să existe calculatoare de uz comun).
Decriptarea este la rîndul ei o problemă NP, dacă o formulăm în felul următor: ``este acest şir de caractere criptarea unui text cu sens''? Decriptarea este în NP, pentru că dacă cineva ne oferă cheia de decriptare, putem obţine textul criptat cu un algoritm rapid; putem astfel verifica în timp polinomial că mesajul criptat este într-adevăr rezultat din sursă.
Dar dacă P=NP, înseamnă că există un algoritm de timp polinomial pentru SAT; îl putem folosi împreună cu metoda auto-reducerii pentru a ``sparge'' orice mesaj! Deci, dacă P=NP, nu există criptografie! Dintr-o dată, lumea arată cu totul altfel.
Pentru că SAT este o problema atît de dificilă multă lume s-a străduit să creeze algoritmi de criptare bazaţi pe probleme NP-complete. Din nefericire pînă la urmă toate metodele de criptare bazate pe probleme NP-complete s-au dovedit a fi foarte uşor de spart!
Asta e chiar o surpriză: creăm probleme dintr-o clasă reputat dificilă, dar în practică reuşim foarte des să le rezolvăm! Nu e ceva putred la mijloc?
De fapt nimic nu ne garantează că NP este o clasă potrivită pentru criptografie, pentru că ``tăria'' oferită de NP nu este aceeaşi cu ``tăria'' necesară criptografilor. Iată de ce: dacă ne ducem la prima parte a acestui articol, vedem că complexitatea unei clase de probleme este dată de cea mai grea problemă din clasă. Astfel, dacă toate problemele din NP ar fi foarte uşoare, dar una singură ar fi extrem de grea, noi tot am declara clasa NP ca fiind grea. Asta se numeşte ``complexitatea în cazul cel mai rău'' (worst-case complexity).
Criptografii pe de altă parte nu vor ca unele probleme să fie grele şi altele uşoare; ei vor ca o problemă aleasă la întîmplare să fie dificilă: nu ai nici un avantaj dacă există o singură cheie care nu poate fi ``spartă'', pentru că este nevoie de multe chei. Complexitatea ``medie'' a unei probleme trebuie să fie ridicată pentru ca acea problemă să fie potrivită pentru criptografie.
Clasa problemelor NP-complete nu pare să fie densă în probleme grele; ea constă în probleme expresive: vă reamintiţi că o problemă este NP-completă dacă putem reduce orice altă problemă din NP la ea; asta înseamnă că ``limbajul'' problemelor NP-complete este foarte expresiv: ne permite să codificăm orice altă problemă.
La ora asta cei mai rezilienţi algoritmi criptografici se bazează pe probleme care nu sunt demonstrate a fi NP-complete, şi care foarte probabil nici nu sunt (dar, din nou, nu există încă nici o demonstraţie în acest sens). Cele mai bune candidate s-au dovedit unele probleme de teoria numerelor. De fapt nişte probleme absolut banale (în sensul că pot fi explicate şi unui şcolar): criptosistemul cu cheie publică RSA se bazează pe problema factorizării: dacă am un număr, cum să-l descompun într-un produs de factori (primi).
Dacă vă grăbiţi să sugeraţi algoritmul învăţat la şcoală pentru descompunere în factori primi, vă invit să-i analizaţi complexitatea. Acel algoritm trebuie să încerce toate numerele prime mai mici decît numărul pe care vreţi să-l descompuneţi. Ori, pentru numărul n, există aproximativ 2n/log(2n) astfel de numere, adică un număr exponenţial. Asta înseamnă că algoritmul, deşi funcţionează binişor pentru numerele oferite în clasă ca exerciţiu, este absolut inaplicabil, chiar cu cele mai performante calculatoare, atunci cînd avem de-a face cu numere de sute de cifre.
O întrebare legitimă pe care ne-o putem pune este ``cînd este o instanţă a lui SAT dificilă''? Pentru a putea răspunde la această întrebare, vom introduce nişte noi elemente de terminologie.
După cum am spus, o problemă din SAT constă într-o formulă booleană (sau un circuit logic) care aplică operaţiile ``sau'', ``şi'' şi ``nu'' logic unor variabile pentru a obţine o singură valoare, de un bit. Ce vrem să ştim este dacă există valori ale variabilelor manipulate care să facă formula ``1''.
Algebra booleană ne învaţă că fiecare formulă logică se poate rescrie într-o formă mai simplă, în care:
O astfel de formă se numeşte ``forma normală conjunctivă'', sau
CNF (Conjunctive Normal Form), pentru că formula este o conjuncţie
(şi) de disjuncţii (sau). De exemplu
![]() este în forma CNF, pe cînd
este în forma CNF, pe cînd
![]() nu este, pentru că avem o negaţie aplicată unei formule.
nu este, pentru că avem o negaţie aplicată unei formule.
Se poate arăta că, chiar dacă formula este exprimată în forma CNF, asta nu simplifică cu nimic sarcina lui SAT, problema rămînînd NP-completă. Poate să vi se pară ciudat că s-ar putea întîmpla altfel: în definitiv orice formulă poate fi scrisă sub forma CNF; aparent noi rezolvăm aceeaşi problemă, doar scrisă diferit: de ce ne-am aştepta ca complexitatea rezolvării să fie alta dacă exprimăm formula altfel?
Ei bine, clasa de probleme depinde foarte mult şi de felul în care enunţăm problema; clasa SAT este diferită de clasa CNF-SAT: prima clasă conţine orice formulă logică, a doua numai formulele logice care sunt scrise în forma normală conjunctivă. E adevărat că orice formulă din prima clasă este absolut echivalentă cu una din a doua clasă (în sensul că calculează aceeaşi funcţie booleană), dar cele două formule nu sunt identice.
Pentru a ne convinge că este important modul de exprimare, să notăm că există şi o formă de scriere a formulelor boolene, numită ``normală disjunctivă'', notată DNF, care e la fel cu CNF, dar la care se schimbă semnele ``sau'' şi ``şi'' între ele. Se poate de asemenea arăta că de asemenea orice formulă booleană se poate pune în forma normală disjunctivă. Dar orice întrebare din DNF-SAT se poate rezolva în timp polinomial! DNF-SAT este o clasă de probleme mult mai uşoare decît cele din SAT sau CNF-SAT.
De ce stau lucrurile aşa? Pentru că atunci cînd transcriem o formulă din SAT în formă DNF-SAT, lungimea ei poate creşte foarte mult; dacă lungimea iniţială a formulei era x şi complexitatea algoritmului era 2x, şi dacă după traducere avem lungimea n=2x şi complexitatea n2 = 2x2, care este exponenţială în x dar polinomială în n.
Iată încă un exemplu: problema de a găsi divizorii unui număr este foarte grea dacă numărul este scris în baza 2 (sau orice altă bază mai mare ca 2), dar este foarte simplă dacă numărul este scris în baza 1. Dacă scriem numărul 100 folosind 100 de beţişoare, atunci putem exhiba un algoritm de complexitate n2 care găseşte toţi divizorii lui 100 (de pildă algoritmul învăţat în şcoala primară). Dar, scriind un număr în baza 2, folosim mult mai puţine cifre (mai exact, pentru n folosim log n cifre), deci chiar dacă aplicăm acelaşi algoritm, într-un caz măsurăm timpul algoritmului relativ la n, iar în altul relativ la log n$.
Din motive tehnice adesea cercetătorii lucrează cu o versiune a
problemei CNF-SAT, descrisă printr-un număr k: k-CNF-SAT. Avem
astfel 2-CNF-SAT, 3-CNF-SAT, etc. Clasa k-CNF-SAT constă din
formulele boolene scrise în formă CNF dar pentru care orice clauză
are cel mult k literali. De exemplu formula
![]() este în 3-CNF-SAT, şi în
4-CNF-SAT, dar nu în 2-CNF-SAT.
este în 3-CNF-SAT, şi în
4-CNF-SAT, dar nu în 2-CNF-SAT.
Se arată de asemenea, fără prea multă dificultate, că, pentru orice k întreg, orice formulă booleană se poate aduce în forma k-CNF-SAT.
Avem însă de a face cu un fenomen interesant: 1- şi 2-CNF-SAT sunt clase de probleme foarte uşoare: se cunoaşte chiar un algoritm de timp linear care rezolvă aceste probleme. Pe de altă parte toate clasele CNF-SAT cu mai mult de doi literali pe clauză sunt NP-complete!
Ce straniu! O diferenţă atît de mare de complexitate, şi o diferenţă atît de mică de formă. Acest fenomen se întîlneşte foarte adesea în teoria NP-complexităţii; sunt foarte multe probleme pentru care o anumită variantă este simplă, dar de îndată ce schimbi un pic enunţul o transformi într-o variantă foarte dificilă. (De exemplu, întrebarea dacă putem colora o hartă cu două culori, în aşa fel încît ţari vecine să nu fie colorate la fel, este banală, dar aceeaşi întrebare cu numărul trei este NP-completă. Ştim că putem oricînd colora o hartă cu 4 culori, dintr-o teoremă extrem de celebră.)
După cum am spus mai sus, nu toate instanţele unor probleme NP-complete sunt la fel de grele: numai cele mai dificile sunt foarte grele; unele pot fi foarte uşoare. Un articol extrem de interesant, care a făcut vîlvă, a asimilat comportarea formulelor boolene cu fenomenele fizice care se petrec cînd un material face o tranziţie de fază, de exemplu de la lichid spre solid. Acest articol este o colaborare între fizicieni şi informaticieni, şi a fost publicat în revista Nature. Articolul este scris de Rémi Monasson, de la laboratorul CNRS de fizică teoretică de la Paris, Riccardo Zecchina, de la Centrul internaţional pentru fizică teoretică de la Trieste, Scott Kirkpatrick, de la laboratoarele T. J. Watson ale lui IBM, Bart Selman, profesor la departamentul de calculatoare de la Universitatea Cornell şi Lidror Troyansky, de la departamentul de calculatoare al universităţii evreieşti din Ierusalim.
Articolul a făcut atîta vîlvă încît a apărut şi în ziare; o
versiune de popularizare despre această temă puteţi găsi de
exemplu în New York Times la
http://www.nytimes.com/library/national/science/071399sci-satisfiability-problems.html.
Articolul studiază care dintre problemele SAT sunt grele şi care sunt uşoare. Cantitatea aflată sub studiu este constrîngerea: cît de multe condiţii sunt puse asupra unei formule. Dacă o formulă este prea puţin constrînsă, are o multitudine de soluţii. Dacă formula este foarte constrînsă, atunci nu are nici o soluţie. Astfel de formule sunt foarte uşor de rezolvat: pentru cele puţin constrînse putem găsi soluţii aproape la întîmplare, pe cele supra-constrînse le putem uşor demonstra ca ne-avînd nici o soluţie. Noţiunea de constrîngere poate fi asimilată cu rangul unui sistem de ecuaţii lineare din algebră: un sistem de ecuaţii care are mai multe variabile decît ecuaţii11 are o infinitate de soluţii, un sistem care are mai multe ecuaţii decît variabile nu are nici o soluţie. Articolul asimilează constrîngerea cu gradul de libertate al moleculelor dintr-un lichid, respectiv solid: solidul este mult mai constrîns.
Constrîngerea poate fi măsurată pentru probleme k-CNF-SAT prin
raportul dintre numărul de clauze din formulă şi numărul de
variabile. Iată intuitiv de ce lucrurile stau aşa: să luăm o
clauză izolată şi să o facem adevărată selectînd un literal
anume ca adevărat (să zicem ca acesta este literalul a). Dacă ne
uităm acum la toate celelalte clauze care conţin ![]() , ele vor
fi forţate să aleagă un alt literal să fie adevărat. Aceste
clauze sunt constrînse de prima, pentru că au mai puţine
alegeri de făcut. Cu cît avem mai multe clauze, cu atît avem mai
multe constrîngeri reciproce.
, ele vor
fi forţate să aleagă un alt literal să fie adevărat. Aceste
clauze sunt constrînse de prima, pentru că au mai puţine
alegeri de făcut. Cu cît avem mai multe clauze, cu atît avem mai
multe constrîngeri reciproce.
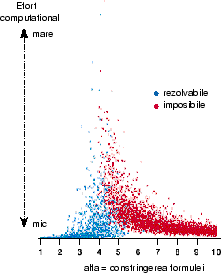
Articolul citat face un studiu experimental asupra raportului ![]() dintre numărul de clauze şi numărul de variabile, folosind formule
generate aleator pe care le rezolvă prin forţă brută. Graficul
din figura 3 arată dependenţa dificultăţii unei probleme
de acest număr. Cînd
dintre numărul de clauze şi numărul de variabile, folosind formule
generate aleator pe care le rezolvă prin forţă brută. Graficul
din figura 3 arată dependenţa dificultăţii unei probleme
de acest număr. Cînd ![]() este un număr mic, problemele au
multe soluţii, şi sunt uşor de rezolvat. Cînd
este un număr mic, problemele au
multe soluţii, şi sunt uşor de rezolvat. Cînd ![]() este mare
problemele nu au nici o soluţie, şi acest lucru este iarăşi foarte
uşor de descoperit. Cînd
este mare
problemele nu au nici o soluţie, şi acest lucru este iarăşi foarte
uşor de descoperit. Cînd ![]() atinge o valoare critică, (care
depinde de k), nu e clar dacă problemele au sau nu soluţii, iar
determinarea acestui lucru este extrem de dificil. Pentru aceste
instanţe, algoritmi cunoscuţi calculează foarte mult.
atinge o valoare critică, (care
depinde de k), nu e clar dacă problemele au sau nu soluţii, iar
determinarea acestui lucru este extrem de dificil. Pentru aceste
instanţe, algoritmi cunoscuţi calculează foarte mult.
 |
Voi încheia excursia în domeniul SAT prin expunerea soluţiilor folosite pentru a rezolva aceste probleme în practică. Faptul că nu putem să rezolvăm problemele în general nu înseamnă că nu avem nevoie să o facem, ba chiar, aşa cum am arătat, probleme NP-complete apar adesea în practică. Aşa că tot ce putem face este să facem tot felul de trucuri care măcar rezolvă rapid cazurile uşoare.
În mod paradoxal, cei mai eficace algoritmi din ziua de azi sunt doar variante ale unor algoritmi deosebit de simpli. Trimitem cititorul interesat la articolul lui Stephen Cook12 şi David Mitchell ``Finding Hard Instances of the Satisfiability Problem: A Survey'', publicată în DIMACS Series in Discrete Mathematics and Computer Science în 1997.
Cel mai eficace algoritm general pentru SAT rămîne un algoritm propus de M. Davis şi H. Putnam în 1960! Algoritmul lor alege succesiv un literal pe care îl face adevărat, după care şterge toate clauzele care conţin acel literal, pentru că aceste clauze sunt deja satisfăcute. În plus, literalul negat este eliminat de peste tot din celelalte clauze, pentru că este deja fals.
Crucială este alegerea literalului, iar algoritmul lor sugerează nişte euristici care duc la rezultate foarte bune în practică. Euristicile sunt reguli care fac un algoritm mai eficient în general, dar despre care nu se poate demonstra că sunt întotdeauna alegerea corectă; sunt deci ``ghiciri înţelepte''.
Metoda lor începe prin a elimina întotdeauna cele mai constrînse clauze, adică cele care conţin un singur literal: este clar că acesta trebuie să fie adevărat pentru a face formula adevărată. Datorită eliminărilor, astfel de clauze apar şi în cursul evoluţiei algoritmului. Dacă nu sunt astfel de clauze, atunci un literal este ales la întîmplare şi se încearcă pe rînd ambele valori posibile, 0 şi 1, făcînd backtracking dacă o încercare eşuează.
Acest algoritm face parte din ceea ce se numesc ``metode incomplete de rezolvare'', pentru că nu funcţionează pe probleme care nu sunt satisfiabile, dar funcţionează excelent pe cele care au soluţii, găsind foarte repede soluţii. Acest algoritm a fost propus de Bart Selman, acum la Universitatea Cornell (şi unul dintre autorii articolului de mai sus despre tranziţiile de fază).
Acest algoritm este foarte surprinzător pentru că este un algoritm aleator: dă cu banul pentru a decide ce valoare trebuie să aibă fiecare variabilă. De fapt acest algoritm este reprezentativ pentru cercetarea curentă în teoria algoritmilor aleatori (pe care i-am menţionat pe larg într-un articol în PC Report din august 1997).
Algoritmul este următorul:
Am văzut în acest articol că există probleme al căror enunţ este banal, dar care sunt de fapt foarte greu de rezolvat în practică în mod eficient. Această stare de fapt simultan ne bucură şi ne întristează: ne bucură pentru că dacă am putea rezolva aceste probleme uşor, ar rezulta că unele din îndeletnicirile umane pe care le preţuim cel mai mult, de exemplu creativitatea matematicienilor, pot fi reduse la simple manipulări mecaniciste. Ne-am întrista, pentru că de fapt ne dorim foarte mult să rezolvăm aceste probleme, fiindcă importanţă lor practică este enormă.
Dacă vă doriţi un drum rapid spre faimă mondială, atunci una dintre soluţii este să rezolvaţi această întrebare: se pot sau nu rezolva aceste probleme în mod eficient, sau, tehnic vorbind, este P tot una cu NP? Dar, fiţi preveniţi, multe capete luminate s-au luptat cu această enigmă şi au fost toate înfrînte!