High priority class has larger mean

In Figure 4.4(a), we once again hold the mean high priority job size fixed at 1 and now assume the low priority job sizes have a mean size of 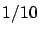$1/10$. That is, we are giving priority to large jobs, which worsen the overall mean response time.

Once again, in the topmost plot of column (a), we see that the preferred number of servers for high priority jobs is unaffected, since the high priority mean job size distribution has not changed. The low priority jobs, shown in the second plot of column (a), have vastly different preferences from the prior case. Here the low priority jobs prefer a large number of servers. Because the low priority jobs are much smaller than the high priority jobs, they want more servers in order to avoid being blocked behind the (large) high priority jobs.

The preferred number of servers for the overall mean response time in the dual-priority system, shown in the third plot of column (a), is again a hybrid of the preferences of the low and high priority jobs, but this time is strongly biased toward the low priority jobs because there are more of them. Notice therefore, that the number of servers preferred is much greater in this case. Comparing this with the single class aggregate, we see that the single class prefers slightly fewer servers than the dual class overall mean. Since larger jobs have higher priority in this case, the multiple servers provide a huge benefit to (small) low priority jobs.

Figure 4.4(b) illustrates the same graphs for the case where the high priority jobs comprise less of the total load. The trends are the same as in column (a); however the preferred number of servers is significantly smaller in all figures. This follows from the same argument as that given for Figure 4.2(b). In the case (not shown) where high priority jobs make up a greater proportion of the total load, more servers are preferable.

Figure 4.5: Mean response time as a function of the number of servers. Here, 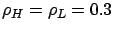$\rho_H = \rho_L = 0.3$ is fixed.

High Priority

Low Priority

Overall mean

1 Aggregate Class

(a) $\mbox{{\bf\sf E}}\left[ X_H \right]=1$ and $\mbox{{\bf\sf E}}\left[ X_L \right] = 10$

(for $k=10$)

(b) $\mbox{{\bf\sf E}}\left[ X_H \right]=1$ and $\mbox{{\bf\sf E}}\left[ X_L \right] = \frac{1}{10}$

(for $k=10$)