



Next: The Mitrani-King-Nishida (MK-N) approximation
Up: Approximations for multiserver systems
Previous: Approximations for multiserver systems
Contents
The BB approximation is based on an intuitive observation that the
``improvement'' of priority scheduling over FCFS scheduling under
multiple servers is similar to that for the case of a single server:
![\begin{displaymath}
\frac{\mbox{{\bf\sf E}}\left[ D^{\mbox{\scriptsize M/GI/}k\m...
...iptsize M/GI/1/FCFS}} \right]} \equiv \mbox{
scaling factor}.
\end{displaymath}](img1263.png) |
(4.2) |
Here
![$\mbox{{\bf\sf E}}\left[ D^{\mbox{\scriptsize M/GI/}k\mbox{\scriptsize /prio}} \right]$](img1256.png) is the
overall mean delay under priority scheduling with
is the
overall mean delay under priority scheduling with  servers of speed
servers of speed
 , and
, and
![$\mbox{{\bf\sf E}}\left[ D^{\mbox{\scriptsize M/GI/}k\mbox{\scriptsize /FCFS}} \right]$](img1258.png) is defined similarly for FCFS.
This relation is exact when job sizes are exponential with the
same mean for all classes.
is defined similarly for FCFS.
This relation is exact when job sizes are exponential with the
same mean for all classes.
Specifically, BB analyzes the mean delay of class  jobs,
jobs,
![$\mbox{{\bf\sf E}}\left[ D_i \right]$](img1265.png) , by analyzing both the mean delay over
classes 1 to
, by analyzing both the mean delay over
classes 1 to  ,
,
![$\mbox{{\bf\sf E}}\left[ D \right]$](img1266.png) , and the mean delay of the higher priority
classes (classes 1 to
, and the mean delay of the higher priority
classes (classes 1 to  ),
),
![$\mbox{{\bf\sf E}}\left[ D_H \right]$](img1267.png) , and then using the following relation:
, and then using the following relation:
where  and
and 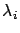 are the arrival rates of the higher
priority classes and class
are the arrival rates of the higher
priority classes and class  jobs, respectively. To compute
jobs, respectively. To compute
![$\mbox{{\bf\sf E}}\left[ D \right]$](img1266.png) (respectively,
(respectively,
![$\mbox{{\bf\sf E}}\left[ D_H \right]$](img1267.png) ), BB aggregates classes 1 to
), BB aggregates classes 1 to  (respectively, classes 1 to
(respectively, classes 1 to  ) into a single class and analyzes
the corresponding M/GI/
) into a single class and analyzes
the corresponding M/GI/ /FCFS queue (e.g. via known approximations
[27,141]), and then calibrates this result using the
scaling factor in (4.2), as shown in (4.1).
/FCFS queue (e.g. via known approximations
[27,141]), and then calibrates this result using the
scaling factor in (4.2), as shown in (4.1).




Next: The Mitrani-King-Nishida (MK-N) approximation
Up: Approximations for multiserver systems
Previous: Approximations for multiserver systems
Contents
Takayuki Osogami
2005-07-19
![\begin{displaymath}
\frac{\mbox{{\bf\sf E}}\left[ D^{\mbox{\scriptsize M/GI/}k\m...
...iptsize M/GI/1/FCFS}} \right]} \equiv \mbox{
scaling factor}.
\end{displaymath}](img1263.png)
![]() jobs,
jobs,
![]() , by analyzing both the mean delay over
classes 1 to
, by analyzing both the mean delay over
classes 1 to ![]() ,
,
![]() , and the mean delay of the higher priority
classes (classes 1 to
, and the mean delay of the higher priority
classes (classes 1 to ![]() ),
),
![]() , and then using the following relation:
, and then using the following relation: