



Next: Mean response time of
Up: The adaptive dual threshold
Previous: The adaptive dual threshold
Contents
Figure 7.10 illustrates static robustness of the ADT
policy, showing the mean response time under the ADT policy (a) as a
function of  and (b) as a function of
and (b) as a function of  . For
comparison, the mean response time under two T1 policies are plotted
with dotted lines. The parameter settings in the middle row are
exactly the same as those in Figure 7.6. In the
top and bottom rows, only the value of
. For
comparison, the mean response time under two T1 policies are plotted
with dotted lines. The parameter settings in the middle row are
exactly the same as those in Figure 7.6. In the
top and bottom rows, only the value of  is changed, as
labeled.
is changed, as
labeled.
Figure 7.10 shows that the ADT policy with parameters
(
 ) achieves at least as low mean response
time as the better of the two T1 policies, one with parameter
) achieves at least as low mean response
time as the better of the two T1 policies, one with parameter
 and the other with parameter
and the other with parameter  , throughout the
range of
, throughout the
range of  and
and  , if
, if  is chosen appropriately. In
plotting Figure 7.10, we found ``good''
is chosen appropriately. In
plotting Figure 7.10, we found ``good''  values
manually by trying a few different values so that the ADT policy
provides low mean response time throughout the range of load, which
took only a few minutes. Observer that if
values
manually by trying a few different values so that the ADT policy
provides low mean response time throughout the range of load, which
took only a few minutes. Observer that if  is set too low, the
ADT policy behaves like the T1 policy with parameter
is set too low, the
ADT policy behaves like the T1 policy with parameter  ,
degrading the mean response time at lower loads, since
,
degrading the mean response time at lower loads, since  is
larger than the optimal
is
larger than the optimal  in the T1 policy at lower loads. If
in the T1 policy at lower loads. If
 is set too high, the ADT policy behaves like the T1 policy with
parameter
is set too high, the ADT policy behaves like the T1 policy with
parameter  . This worsens the mean response time at higher
loads.
. This worsens the mean response time at higher
loads.
Static robustness of the ADT policy can be attributed to the following.
The dual thresholds on queue 1 make the ADT policy
adaptive to misestimation of load, in that the ADT policy with
parameters (
 ) operates like the T1
policy with parameter
) operates like the T1
policy with parameter  at the estimated load and like the
T1 policy with parameter
at the estimated load and like the
T1 policy with parameter  at a higher load, where
at a higher load, where
 .
Thus, server 2 can help queue 1
less when there are more type 2 jobs, preventing server 2 from
becoming overloaded. This leads to the increased stability
region and improved performance.
.
Thus, server 2 can help queue 1
less when there are more type 2 jobs, preventing server 2 from
becoming overloaded. This leads to the increased stability
region and improved performance.
Figure 7.10 makes an additional point about the effect of
 . When
. When  is smaller (top row), the difference in
the stability regions of the two T1 policies becomes smaller, and the
difference in the mean response times of the two T1 policies at low
loads becomes larger. Thus, the benefit of the ADT policy over the T1
policy becomes smaller at smaller
is smaller (top row), the difference in
the stability regions of the two T1 policies becomes smaller, and the
difference in the mean response times of the two T1 policies at low
loads becomes larger. Thus, the benefit of the ADT policy over the T1
policy becomes smaller at smaller  , since the T1 policy with
smaller
, since the T1 policy with
smaller  can provide low mean response time with only a slightly
reduced stability region. This makes intuitive sense, since in the
limit as
can provide low mean response time with only a slightly
reduced stability region. This makes intuitive sense, since in the
limit as
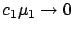 , the Beneficiary-Donor model reduces to a single
(donor) server with two queues, where the policy following the
, the Beneficiary-Donor model reduces to a single
(donor) server with two queues, where the policy following the  rule is
provably optimal [45].
Also, when
rule is
provably optimal [45].
Also, when  is larger (bottom row),
the difference in the stability region of the two T1 policies becomes
larger, and the difference in the mean response times of the two
T1 policies at low loads becomes smaller.
Again, the benefit of the ADT policy over the T1
policy becomes smaller at larger
is larger (bottom row),
the difference in the stability region of the two T1 policies becomes
larger, and the difference in the mean response times of the two
T1 policies at low loads becomes smaller.
Again, the benefit of the ADT policy over the T1
policy becomes smaller at larger  , since the T1 policy with
larger
, since the T1 policy with
larger  can provide a wide stability region with
only a slightly high mean response time at lower loads.
This makes intuitive sense, since
the jobs in queue 1 are much better served by server 1 and
the help from server 2 becomes negligible when
can provide a wide stability region with
only a slightly high mean response time at lower loads.
This makes intuitive sense, since
the jobs in queue 1 are much better served by server 1 and
the help from server 2 becomes negligible when  is much larger
than
is much larger
than  .
Thus, the ADT policy is most effective when
.
Thus, the ADT policy is most effective when  and
and  are comparable and
are comparable and
 ,
where the T1 policy with
,
where the T1 policy with  provides lower mean response time
than T1(1) and T1(
provides lower mean response time
than T1(1) and T1( ) but suffers from static robustness.
) but suffers from static robustness.




Next: Mean response time of
Up: The adaptive dual threshold
Previous: The adaptive dual threshold
Contents
Takayuki Osogami
2005-07-19
![]() and (b) as a function of
and (b) as a function of ![]() . For
comparison, the mean response time under two T1 policies are plotted
with dotted lines. The parameter settings in the middle row are
exactly the same as those in Figure 7.6. In the
top and bottom rows, only the value of
. For
comparison, the mean response time under two T1 policies are plotted
with dotted lines. The parameter settings in the middle row are
exactly the same as those in Figure 7.6. In the
top and bottom rows, only the value of ![]() is changed, as
labeled.
is changed, as
labeled.
![]() ) achieves at least as low mean response
time as the better of the two T1 policies, one with parameter
) achieves at least as low mean response
time as the better of the two T1 policies, one with parameter
![]() and the other with parameter
and the other with parameter ![]() , throughout the
range of
, throughout the
range of ![]() and
and ![]() , if
, if ![]() is chosen appropriately. In
plotting Figure 7.10, we found ``good''
is chosen appropriately. In
plotting Figure 7.10, we found ``good'' ![]() values
manually by trying a few different values so that the ADT policy
provides low mean response time throughout the range of load, which
took only a few minutes. Observer that if
values
manually by trying a few different values so that the ADT policy
provides low mean response time throughout the range of load, which
took only a few minutes. Observer that if ![]() is set too low, the
ADT policy behaves like the T1 policy with parameter
is set too low, the
ADT policy behaves like the T1 policy with parameter ![]() ,
degrading the mean response time at lower loads, since
,
degrading the mean response time at lower loads, since ![]() is
larger than the optimal
is
larger than the optimal ![]() in the T1 policy at lower loads. If
in the T1 policy at lower loads. If
![]() is set too high, the ADT policy behaves like the T1 policy with
parameter
is set too high, the ADT policy behaves like the T1 policy with
parameter ![]() . This worsens the mean response time at higher
loads.
. This worsens the mean response time at higher
loads.
![]() ) operates like the T1
policy with parameter
) operates like the T1
policy with parameter ![]() at the estimated load and like the
T1 policy with parameter
at the estimated load and like the
T1 policy with parameter ![]() at a higher load, where
at a higher load, where
![]() .
Thus, server 2 can help queue 1
less when there are more type 2 jobs, preventing server 2 from
becoming overloaded. This leads to the increased stability
region and improved performance.
.
Thus, server 2 can help queue 1
less when there are more type 2 jobs, preventing server 2 from
becoming overloaded. This leads to the increased stability
region and improved performance.
![]() . When
. When ![]() is smaller (top row), the difference in
the stability regions of the two T1 policies becomes smaller, and the
difference in the mean response times of the two T1 policies at low
loads becomes larger. Thus, the benefit of the ADT policy over the T1
policy becomes smaller at smaller
is smaller (top row), the difference in
the stability regions of the two T1 policies becomes smaller, and the
difference in the mean response times of the two T1 policies at low
loads becomes larger. Thus, the benefit of the ADT policy over the T1
policy becomes smaller at smaller ![]() , since the T1 policy with
smaller
, since the T1 policy with
smaller ![]() can provide low mean response time with only a slightly
reduced stability region. This makes intuitive sense, since in the
limit as
can provide low mean response time with only a slightly
reduced stability region. This makes intuitive sense, since in the
limit as
![]() , the Beneficiary-Donor model reduces to a single
(donor) server with two queues, where the policy following the
, the Beneficiary-Donor model reduces to a single
(donor) server with two queues, where the policy following the ![]() rule is
provably optimal [45].
Also, when
rule is
provably optimal [45].
Also, when ![]() is larger (bottom row),
the difference in the stability region of the two T1 policies becomes
larger, and the difference in the mean response times of the two
T1 policies at low loads becomes smaller.
Again, the benefit of the ADT policy over the T1
policy becomes smaller at larger
is larger (bottom row),
the difference in the stability region of the two T1 policies becomes
larger, and the difference in the mean response times of the two
T1 policies at low loads becomes smaller.
Again, the benefit of the ADT policy over the T1
policy becomes smaller at larger ![]() , since the T1 policy with
larger
, since the T1 policy with
larger ![]() can provide a wide stability region with
only a slightly high mean response time at lower loads.
This makes intuitive sense, since
the jobs in queue 1 are much better served by server 1 and
the help from server 2 becomes negligible when
can provide a wide stability region with
only a slightly high mean response time at lower loads.
This makes intuitive sense, since
the jobs in queue 1 are much better served by server 1 and
the help from server 2 becomes negligible when ![]() is much larger
than
is much larger
than ![]() .
Thus, the ADT policy is most effective when
.
Thus, the ADT policy is most effective when ![]() and
and ![]() are comparable and
are comparable and
![]() ,
where the T1 policy with
,
where the T1 policy with ![]() provides lower mean response time
than T1(1) and T1(
provides lower mean response time
than T1(1) and T1(![]() ) but suffers from static robustness.
) but suffers from static robustness.