



Next: Properties of Markovian arrival
Up: Bibliography
Previous: Proof of Theorem 11
Contents
Moment matching algorithm by Bobbio, Horváth, and Telek
In this section, we summarize the recent results by Bobbio et al.
[22] on characterization of PH distributions and moment
matching algorithms, which build upon our results in
Chapter 2. Recall that
 denotes the set
of distributions that are well represented by an
denotes the set
of distributions that are well represented by an  -phase acyclic PH
distribution (Definition 5). Bobbio et al. provide
exact conditions for a distribution
-phase acyclic PH
distribution (Definition 5). Bobbio et al. provide
exact conditions for a distribution  to be in set
to be in set
 (see Theorem 21)
as well as exact conditions for
(see Theorem 21)
as well as exact conditions for
 (see Theorem 20), where
(see Theorem 20), where
 is defined as follows:
is defined as follows:
Definition 20
Let
 denote the set of distributions that are
well-represented by an
denote the set of distributions that are
well-represented by an  -phase acyclic PH distribution
with no mass probability at zero for positive
integer
-phase acyclic PH distribution
with no mass probability at zero for positive
integer  .
.
Further, Bobbio et al. provide a closed form solution for mapping
any
 to a minimal-phase acyclic PH distribution without
mass probability at zeroB.1 (see Theorem 22).
As we define the EC distribution and map an input distribution
to an EC distribution in Chapter 2, Bobbio et al. also define a subset
of PH distributions, and map an input distribution to
a PH distribution in the subset.
Specifically, Bobbio et al. map an input distribution
to an Erlang-Exp distribution (see Figure B.1) or an Exp-Erlang distribution
(see Figure B.2).
to a minimal-phase acyclic PH distribution without
mass probability at zeroB.1 (see Theorem 22).
As we define the EC distribution and map an input distribution
to an EC distribution in Chapter 2, Bobbio et al. also define a subset
of PH distributions, and map an input distribution to
a PH distribution in the subset.
Specifically, Bobbio et al. map an input distribution
to an Erlang-Exp distribution (see Figure B.1) or an Exp-Erlang distribution
(see Figure B.2).
Figure B.1:
The Markov chain whose absorption time defines an Erlang-Exp distribution.
|
|
Figure B.2:
The Markov chain whose absorption time defines an Exp-Erlang distribution.
|
|
Theorem 20
[22]
A distribution  is in set
is in set
 iff its normalized moments
iff its normalized moments
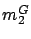 and
and  satisfy the following conditions:
and
where
satisfy the following conditions:
and
where  and
and  are defined as follows:
where
are defined as follows:
where
Theorem 21
[22]
A distribution  is in set
is in set
 iff its normalized moments
iff its normalized moments
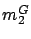 and
and  satisfy the following conditions:
and
where
satisfy the following conditions:
and
where  is the same as in Theorem 20.
is the same as in Theorem 20.




Next: Properties of Markovian arrival
Up: Bibliography
Previous: Proof of Theorem 11
Contents
Takayuki Osogami
2005-07-19






