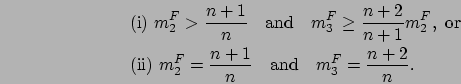Next: Summary of results
Up: Characterizing phase type distributions
Previous: Characterizing phase type distributions
Contents
While our goal is to characterize the set
 , this
characterization turns out to be ugly. One of the key ideas is
that there is a set
, this
characterization turns out to be ugly. One of the key ideas is
that there is a set
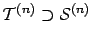 which is
very close to
which is
very close to
 in size, such that
in size, such that
 has a
simple specification.
To provide a simple specification of
has a
simple specification.
To provide a simple specification of
 ,
we define an alternative to the
standard moments, which we refer to as normalized moments:
,
we define an alternative to the
standard moments, which we refer to as normalized moments:
Notice the relationship between the normalized moments and the coefficient of variability 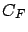 and
the skewness
and
the skewness
 of
of  :
:
where
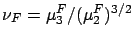 .
(
.
(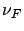 and
and  are closely related,
since
are closely related,
since
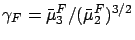 , where
, where
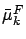 is the centralized
is the centralized  -th moment of
-th moment of  for
for  .)
.)
Now,
 can be defined via normalized moments (see Figure 2.4).
can be defined via normalized moments (see Figure 2.4).
Definition 7
For integers  , let
, let
 denote the set of
distributions,
denote the set of
distributions,  , that satisfy exactly one of the following two conditions:
, that satisfy exactly one of the following two conditions:




Next: Summary of results
Up: Characterizing phase type distributions
Previous: Characterizing phase type distributions
Contents
Takayuki Osogami
2005-07-19
![]() , this
characterization turns out to be ugly. One of the key ideas is
that there is a set
, this
characterization turns out to be ugly. One of the key ideas is
that there is a set
![]() which is
very close to
which is
very close to
![]() in size, such that
in size, such that
![]() has a
simple specification.
To provide a simple specification of
has a
simple specification.
To provide a simple specification of
![]() ,
we define an alternative to the
standard moments, which we refer to as normalized moments:
,
we define an alternative to the
standard moments, which we refer to as normalized moments:
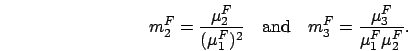
![\includegraphics[width=.4\linewidth]{fig/setT.eps}](img106.png)
![]() can be defined via normalized moments (see Figure 2.4).
can be defined via normalized moments (see Figure 2.4).