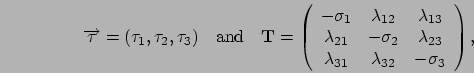Next: Subclasses of PH distribution
Up: Brief tutorial on phase
Previous: Examples of PH distributions
Contents
In general, a PH distribution is the distribution of the time
until absorption into state 0 in a Markov chain.
Figure 2.7:
A three-phase PH distribution.
|
|
Figure 2.7 illustrates a three phase PH distribution
having parameters
where
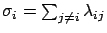 for
for 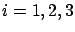 .
Note that the initial state can be the absorption state (state 0) with
positive probability. If the initial state is the absorption state,
the absorption time is zero.
.
Note that the initial state can be the absorption state (state 0) with
positive probability. If the initial state is the absorption state,
the absorption time is zero.
Takayuki Osogami
2005-07-19
![\includegraphics[width=.45\linewidth]{fig/PH3_distribution.eps}](img134.png)