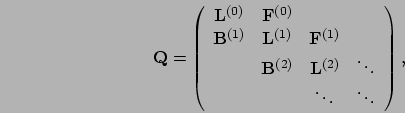Next: Approximations of dimensionality reduction
Up: Dimensionality reduction
Previous: Analysis of the GFB
Contents
Constructing a 1D Markov chain using an approximate background process
In Section 3.5.2, we obtain the generator matrix of an approximate
background process  ,
,
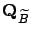 .
In this section, we derive the generator matrix of the 1D Markov chain
reduced from the FB process by replacing the background process
.
In this section, we derive the generator matrix of the 1D Markov chain
reduced from the FB process by replacing the background process  by
by  .
.
We first introduce notations for the generator matrices of the foreground process
conditioned on the level of the background process.
Let
 be the generator matrix of the foreground process,
be the generator matrix of the foreground process,  ,
given that the background process is in level
,
given that the background process is in level  .
As the foreground process is a QBD process given the level of
.
As the foreground process is a QBD process given the level of  ,
,
 is of the form
is of the form
for
 . Recall that the generator matrix of the foreground process
when the background process is in levels
. Recall that the generator matrix of the foreground process
when the background process is in levels 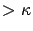 is the same as
is the same as
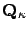 .
.
The 1D Markov chain reduced from the FB process is also a QBD process, and
its generator matrix,  , is given by
, is given by
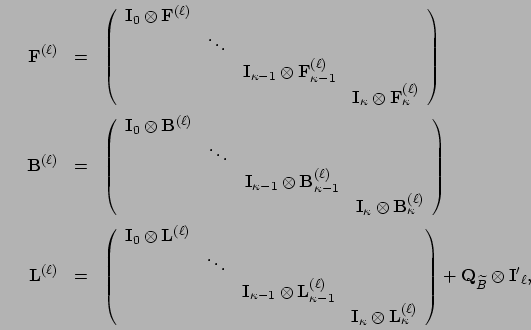
where
for each  ,
where
,
where 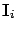 is an identity matrix of order equal to the number of states in level
is an identity matrix of order equal to the number of states in level  of
of  for
for
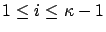 ,
,
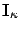 is an identity matrix of order equal to the number of states
corresponding to the collection of PH distributions in
is an identity matrix of order equal to the number of states
corresponding to the collection of PH distributions in  (i.e., when the busy period, the sojourn time in levels
(i.e., when the busy period, the sojourn time in levels  , is approximated by
, is approximated by  PH distributions each with
PH distributions each with  phases,
phases,
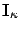 is an
is an  identity matrix),
and
identity matrix),
and
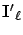 is the number of states in level
is the number of states in level  of
of  for
for  .
.




Next: Approximations of dimensionality reduction
Up: Dimensionality reduction
Previous: Analysis of the GFB
Contents
Takayuki Osogami
2005-07-19
![]() be the generator matrix of the foreground process,
be the generator matrix of the foreground process, ![]() ,
given that the background process is in level
,
given that the background process is in level ![]() .
As the foreground process is a QBD process given the level of
.
As the foreground process is a QBD process given the level of ![]() ,
,
![]() is of the form
is of the form
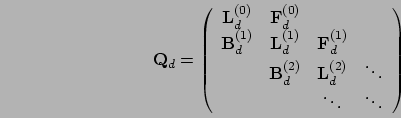
![]() , is given by
, is given by