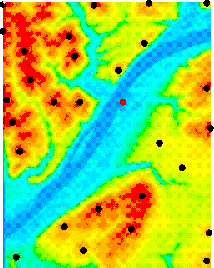
Figure 3: Topographic map of the Pittsburgh area with detected mountains
A variety of methods can be used to determine position, some using internal measurements (dead reckoning) or external measurements of motion. Since dead reckoning degrades over time, external measurements are necessary. A mobile robot performing a long traverse on the Moon or other celestial bodies poses a great challenge for position estimation technologies, due to the absence of the GPS infrastructure. On celestial bodies, attitude measurements can be generated accurately from a star sensor, since the visibility of stars from bodies without atmosphere is excellent, but position accuracy is low, on the order of kilometers [19]. In short, relative position and absolute orientation are available, but absolute position is not.
Our system uses mountains to fix position, as usually done by human sailors in marine navigation. Other researchers have studied the possibility of vision-based localization in outdoor applications [4, 8, 13, 16, 17], but real data analysis has been scarce (the only available data sets have been produced by Thompson and his group [17]), probably due to the complexity of collecting outdoor imagery coupled with reliable ground-truth data. In this paper we present a rich collection of images obtained by a customized platform, which allows us to tag every image with six dimensional ground-truth (position and orientation).
Each image feature can be converted to an angle in the robot's coordinate system; the angle is called a bearing [2]. The image contains a set R of m image bearings. The map contains a number n of landmarks lj = [Xj,Yj]. The pose of the robot in the global coordinate system is Gamma= [x,y,phi] (phi is orientation). An interpretation I of the image is a set of correspondences between image features and map features.
To be able to construct an interpretation, the system must have information about the position of mountains in a topographic map of the rover's environment. To test our system with Earth images, we use 7.5 minute Digital Elevation Maps (DEMs) provided by the United States Geographical Survey (USGS), covering approximately 140km2. Topographic maps are pre-processed and mountains in such maps are marked in an off-line stage, which automatically detects local maxima in the 7.5 minute DEM [18]. For example, the map in Figure 3 covers approximately 37 km2 over the city of Pittsburgh, Pennsylvania. The black dots indicate the points where the system found mountains. The user has the ability to change or correct mountains detected at this stage, but we have never had to do that to obtain our results.

Figure 3: Topographic map of the Pittsburgh area with detected mountains
As the images are received by the system, mountains must be detected and position estimates have to be generated. Currently we do not operate directly on a stream of video; individual images are selected from the video window and manually pasted into a mosaic [15]. The mountain detector works on the mosaics. The mosaic is first segmented in two regions, one corresponding to the sky, another to the ground, and then the boundary between the two regions is searched for mountains. The theory and implementation of this mountain detector was described in a previous publication [2], together with preliminary results. Here we concentrate on a description of results obtained with a more comprehensive set of tests. The mountain detection system takes at most 2 seconds per full panorama in the current implementation on a Silicon Graphics workstation, depending on the complexity of the scenes.
Figure 4 shows a gallery of panoramas processed by our system. Images come from Pennsylvania, Utah, California and the Apollo 17 site on the Moon. Detected mountains are enclosed in rectangles; the detected position of a mountain peak is marked through a vertical line inside the rectangle.
The panorama (1) composes a sequence of images taken by the Apollo 17 Lander Module. The lunar cart can be seen at the extreme right of the panorama. The first large structure is the South Massif, followed by two smaller mountains and then the North Massif. The system detects all of those mountains plus a smaller formation which follows the North Massif. For lunar images, we have found that a very simple thresholding operation is enough to segment the sky from the ground reliably; that was used in panorama (1).
Panoramas (2) and (3) bring images from California; the first is by the Don Pedro Resort and the second is by the East entrance of the Niles Canyon. Mountains are very distinct in the Don Pedro area, but not so in the Niles Canyon. The large structures in this latter panorama are captured, but the peak in the extreme right has a skewed position because of trees on the top of the mountain. These images were acquired under bright sunlight, and the resulting panoramas suffer some effects of the camera's auto-iris operation: the sky shows ``waves'' of high brightness. This would make it impossible to use a simple thresholding operation as in the lunar images, but our sky segmentation algorithm [2] works without problems.
Panoramas (4) and (5) were acquired by Prof. William Thompson and his group and are publicly available. The detector has no problems, except in the detection of very small sequences of mountains that are quite distant.
Panoramas (6), (7) and (8) were obtained in Pittsburgh, by the Allegheny river. All distinct mountains are detected, except the big mountain in panorama (6), where the system gets confused by the pole in the extreme left. The system has proven to be quite reliable and flexible to adjustments, but some occasional misses or false detections occur as a result of unforeseen events like the pole in panorama (6). We plan to give some latitude to the operator, so that the system's conclusions can be modified when mistakes occur.
Figure 4: Peak detection results from a wide variety of scenes
 © Fabio Cozman[Send Mail?]
© Fabio Cozman[Send Mail?] Tue Jun 24 00:46:56 EDT 1997