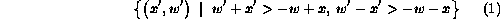
Any standard representation of a rectangle is a four dimensional vector, although it is prudent to note that the space of all rectangles does not map one-to-one mapping with four-space. If the representation consists of the coordinates of the upper left corner plus a width and height, then width and height are constrained to be positive. If the representation is made with two opposing corners of a rectangle, then the points can be listed in either order. The representation we will use consists of the rectangle center point and the half-width and half-height. This change of representation was proposed in [7], although similar methods have been used in the past. To see why this representation is advantageous, we will examine the one dimensional case.
When examining the intersection of intervals, it is useful to view an interval as a point in two-dimensional space. As with the rectangle, let the interval be parameterized by its center point x and its half-length w. Then the set of all intervals which intersect a particular interval can be shown to be:
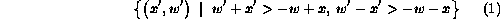
The set of all intervals which are completely contained within a particular interval can similarly be shown to be:
These relations are shown graphically in Figure 1.
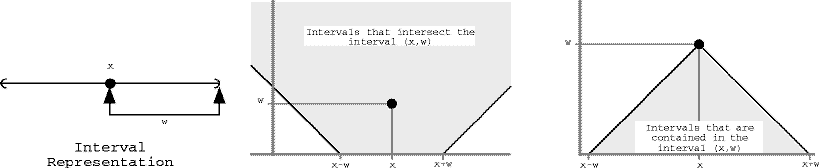
: Geometrical representation of interval intersection and containment.
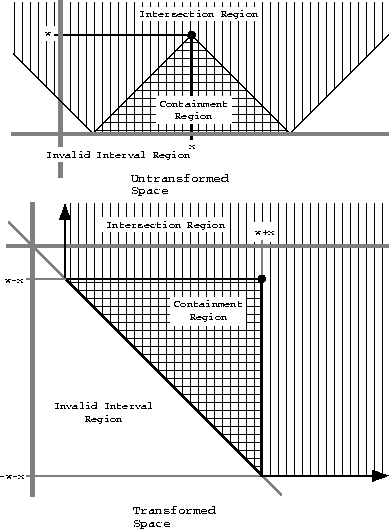
Figure 2: Result of performing a 45 degree rotation on the 
interval space.
This can be derived either geometrically or using linear systems. If the space of the (x,w) vector is rotated by 45 degrees clockwise, a simple interpretation arises. The transformed space is described by the vector:
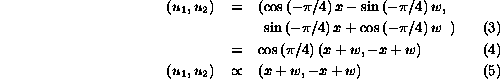
Since the 
is a constant affecting the global scale of all intervals, we can perform the desired rotation without regard to scale and just drop that term.
Figure 2 shows the consequence of this rotation.
The regions labeled invalid intervals correspond to the space of intervals with negative width, and as such, no valid intervals can be represented in that space.
Looking back at equations 1 and 2, the problem of interval intersection and containment has now been reduced to a vector dominance problem, where 
implies that 
for all elements of the vectors 
and 
. In a sense, the rotation has made the problem easier to solve.
To move from intervals to rectangular regions, we move to a four dimensional vector 
.
Point data can be represented by using a zero width and height rectangle.
Line segments can be represented by their bounding rectangle plus one additional bit that signifies the orientation of the line segment, upper left to lower right corner or upper right to lower left corner.
The final transformation applied to all rectangles which are to be stored in the system gives the vector:
To check for rectangles that are completely contained within the 
test rectangle,
apply the transform (6) to the test rectangle and create 
, then look for all 
.
To check for rectangles that intersect the 
rectangle, create 
and look for all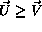 
.