


Next: Empirical Results
Up: Object Manipulation for Document
Previous: Representation of Rectangles
Since we have reduced the question of rectangle intersection and containment to vector dominance, we now need a dynamic algorithm for performing range searches on multidimensional vectors. This comes to us from [8] in a structure called Divided K-D trees.
The idea is to recursively partition the space into regions along one dimension at a time so that each region contains roughly the same number of vectors.
In other words, the first set of divisions is based solely on a single element of the vector.
A second set of divisions based on another vector element is done for each of the top level divisions.
This recursive division is done for three out of four elements of the vector.
Figure 3 shows how the first two of these divisions might look for a set of vectors, which are shown projectioned onto a two dimensional plane.
After all the regions have been recursively formed, the vectors are sorted along the single remaining dimension within their region.
This comes to us from [8] in a structure called Divided K-D trees.
The idea is to recursively partition the space into regions along one dimension at a time so that each region contains roughly the same number of vectors.
In other words, the first set of divisions is based solely on a single element of the vector.
A second set of divisions based on another vector element is done for each of the top level divisions.
This recursive division is done for three out of four elements of the vector.
Figure 3 shows how the first two of these divisions might look for a set of vectors, which are shown projectioned onto a two dimensional plane.
After all the regions have been recursively formed, the vectors are sorted along the single remaining dimension within their region.
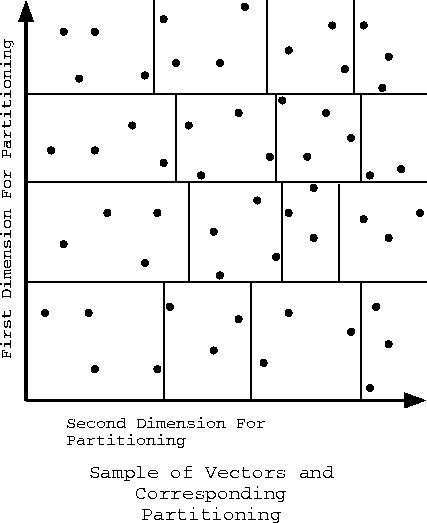
Figure 3: A sample set of vectors and a partitioning into regions.
The storage of this structure is implemented as a multi-level search tree.
The first level of the tree corresponds to the first set of divisions within the first dimension.
Each node of the top level tree corresponds to one region and contains another tree, which partitions the remaining points along a second dimension.
Yet another tree of regions is held by each of the nodes of the second level trees.
The lowest level tree contains the actual vector elements, sorted along the remaining dimension.
The trees have the following constraints placed on them:
1) Any upper level tree, (the first three levels of trees,) partitions the vectors into  distinct regions, each corresponding to a single node in the tree.
2) Each of the bottom level trees contain
distinct regions, each corresponding to a single node in the tree.
2) Each of the bottom level trees contain 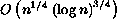 vectors.
By examination, we see that the total number of bottom level trees is
vectors.
By examination, we see that the total number of bottom level trees is  .
.
For the actual implementation, a dynamic binary tree algorithm that gives 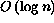 performance for insertion and deletion is needed.
We used the Splay tree data structure from [9], although other structures such as the 2-3 tree could also be used.
performance for insertion and deletion is needed.
We used the Splay tree data structure from [9], although other structures such as the 2-3 tree could also be used.
Balance for the tree is maintained as follows: If an insertion is done in which a bottom level tree, at the fourth layer, grows bigger than 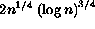 , that tree is split into two regions, creating one additional node in the tree one level up, at the third layer.
If adding one additinal node at the second or higher layers causes that tree to become larger than
, that tree is split into two regions, creating one additional node in the tree one level up, at the third layer.
If adding one additinal node at the second or higher layers causes that tree to become larger than  nodes, then that entire sub-tree, including all the child sub-trees, is rebuilt into two new trees, causing a new node to be inserted in the layer above.
This causes the entire tree is rebuilt when the top level tree has more than
nodes, then that entire sub-tree, including all the child sub-trees, is rebuilt into two new trees, causing a new node to be inserted in the layer above.
This causes the entire tree is rebuilt when the top level tree has more than 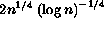 nodes.
nodes.
We will only present the timing results for insertions, deletions and range queries.
For a complete derivation of the d-dimensional case, see [8].
- The cost to insert or delete a single element is an amortized
 .
.
- The cost to perform an exact match query is an amortized
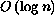 .
.
- The cost to perform a range query is an amortized
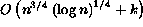 , where k is the number of items found in the range.
, where k is the number of items found in the range.



Next: Empirical Results
Up: Object Manipulation for Document
Previous: Representation of Rectangles
Richard Romero
Tue Jun 13 19:49:23 EDT 1995
 This comes to us from [8] in a structure called Divided K-D trees.
The idea is to recursively partition the space into regions along one dimension at a time so that each region contains roughly the same number of vectors.
In other words, the first set of divisions is based solely on a single element of the vector.
A second set of divisions based on another vector element is done for each of the top level divisions.
This recursive division is done for three out of four elements of the vector.
Figure 3 shows how the first two of these divisions might look for a set of vectors, which are shown projectioned onto a two dimensional plane.
After all the regions have been recursively formed, the vectors are sorted along the single remaining dimension within their region.
This comes to us from [8] in a structure called Divided K-D trees.
The idea is to recursively partition the space into regions along one dimension at a time so that each region contains roughly the same number of vectors.
In other words, the first set of divisions is based solely on a single element of the vector.
A second set of divisions based on another vector element is done for each of the top level divisions.
This recursive division is done for three out of four elements of the vector.
Figure 3 shows how the first two of these divisions might look for a set of vectors, which are shown projectioned onto a two dimensional plane.
After all the regions have been recursively formed, the vectors are sorted along the single remaining dimension within their region.




 distinct regions, each corresponding to a single node in the tree.
2) Each of the bottom level trees contain
distinct regions, each corresponding to a single node in the tree.
2) Each of the bottom level trees contain 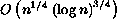 vectors.
By examination, we see that the total number of bottom level trees is
vectors.
By examination, we see that the total number of bottom level trees is  .
.
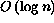 performance for insertion and deletion is needed.
We used the Splay tree data structure from [
performance for insertion and deletion is needed.
We used the Splay tree data structure from [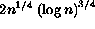 , that tree is split into two regions, creating one additional node in the tree one level up, at the third layer.
If adding one additinal node at the second or higher layers causes that tree to become larger than
, that tree is split into two regions, creating one additional node in the tree one level up, at the third layer.
If adding one additinal node at the second or higher layers causes that tree to become larger than  nodes, then that entire sub-tree, including all the child sub-trees, is rebuilt into two new trees, causing a new node to be inserted in the layer above.
This causes the entire tree is rebuilt when the top level tree has more than
nodes, then that entire sub-tree, including all the child sub-trees, is rebuilt into two new trees, causing a new node to be inserted in the layer above.
This causes the entire tree is rebuilt when the top level tree has more than 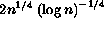 nodes.
nodes.
 .
.
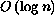 .
.
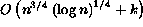 , where k is the number of items found in the range.
, where k is the number of items found in the range.