

Next: Fat Sets
Up: Invariants
Previous: C. Use a proof
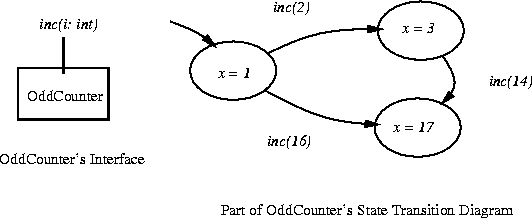
Let OddCounter be the state machine:
More precisely,
OddCounter = (
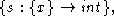
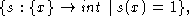
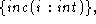
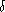 =
=
1
incĒ(i: int)
pre i is even
post x' = x + i
The invariant I want to prove is that OddCounter's
state always holds an odd integer:
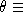 x is odd.
x is odd.
Intuitively we see this
is true because
- It's true of the initial state (1 is an odd integer).
- For the action inc:
- I assume:
- i is even (i.e., the pre-condition holds in the pre-state),
- x is odd (i.e., the invariant holds in the pre-state), and
- x' = x + i (i.e., the post-condition holds in the pre- and post-states)
- I need to show that x' is odd.
- This is true since
from facts about numbers I know an odd number (x) plus an even number (i) is always odd.
Norman Papernick
Mon Mar 18 14:28:12 EST 1996

![]()
![]()
![]()
![]() =
= ![]() x is odd.
x is odd.