15-883 Modeling Project

Computational Models of Neural Systems, Fall 2021

In this project you will replicate the short-term persistent spiking buffer model of entorhinal cortex described by Randal A. Koene and Michael E. Hasselmo in a series of recent papers. The project is divided into a series of steps; we will discuss one step during each class period, and you'll have the opportunity to ask questions and get help if you get stuck. Therefore, try to keep up with the steps; don't leave everything to the last minute.

You are required to write your own code for this project. While you may discuss the project with your fellow students, you may not borrow code from anyone else.

First Step

Read these two key papers describing the model:

Koene, R. A. and Hasselmo, M. E. (2007) First-in-first-out item replacement in a model of short-term memory based on persistent spiking. Cerebral Cortex 17:1766-1781.
Koene, R. A. and Hasselmo, M. E. (2008) Consequences of parameter differences in a model of short-term persistent spiking buffers provided by pyramidal cells in entorhinal cortex. Brain Research 1202:54-67.

Additional papers related to the model you may find useful:

Koene, R. A. and Hasselmo, M. E. (2005) An integrate-and-fire model of prefrontal cortex neuronal activity during performance of goal-directed decision making. Cerebral Cortex 15:1964-1981.
Koene, R. A. and Hasselmo, M. E. (2008) Reversed and forward buffering of behavioral spike sequences enables retrospective and prospective retrieval in hippocampal regions CA3 and CA1. Neural Networks 21(2-3):276-288.

Equation (5) for t_max in the 2007 Cerebral Cortex paper is wrong. Derive the correct equation for t_max by setting the derivative of g_i(t) to zero and solving for t. What do you think led to the error in the paper?

Second Step

Write code to plot the conductance function g_i(t) for any of the pyramidal cell currents listed in Table 1 in the appendix to the Brain Research paper. (Plot the conductance values between 0 and 500 ms and assume a spike occurs at 25 ms.) Also plot the calculated value of t_max as a vertical line. Note: you will discover a problem with the equations when you do this. Come up with a solution.

Another problem has to do with the leak current. The leak conductance is constant; there is no rise or fall. The paper shows a t_fall value of 9 msec because this is a nice trick for getting the conductance to come out to the desired value of 111 nS; it shows no t_rise value. When writing your g_i conductance function you will need to handle the leak current as a special case. You can set its t_rise to NaN when you define the current to mark this case.

Third Step

Create a data structure to describe the various currents that make up a pyramidal cell, most of which are listed in Table 1. For example, you might use a struct array named currents whose first entry, for the AHP current, looks like this:

c.AHP = 1;
currents(c.AHP).tau_rise = 1e-4;
currents(c.AHP).tau_fall = 30;
currents(c.AHP).G = 23;
currents(c.AHP).Erev = -90;
currents(c.AHP).anorm = find_anorm(currents(c.AHP));

In this example, find_anorm is a function that computes anorm, which is a function of t_max. You will find it advantageous to declare c and currents to be global variables. Also, read this page of modeling advice for info on how to structure your MATLAB code.

NOTE: Changes to parameter values: For the ADP current, use tau_rise = 135 - 1e-4, and tau_fall = 135. For the theta current, use tau_fall = 8. For the gamma current, use G=150.

The table of parameters in the paper shows the leak conductance as 111, but the text says that g_leak = C/τ_leak, which might lead you to infer that the value should be 1/9 = 0.111. They messed up on the units. The 111 value is correct. In general, don't worry about getting the units right; just use the numbers in Table 1.

Create a struct array to describe the set of pyramidal cells in your model. Two values you must keep for each cell are: its current membrane voltage V, and the time it last emitted a spike. You may wish to keep additional values around, such as a state indicator (normal, spiking, or refractory), the cell's current total conductance, and the most recent voltage adjustment, ΔV.

At the start of your simulation you will specify the number of pyramidal cells P, and the length of the simulation run in milliseconds. Assume that time starts at t=0 and advances in increments of Δt = 1 msec. From this you can calculate the number of steps S in the simulation. Create a history array Vhist of size P × S that will hold the membrane voltage of each pyramidal cell at each time step. You will use Vhist for plotting the results of your simulation.

Write a function updatePyramid(p,t) where p is the pyramidal cell number (from 1 to P) and t is the current time step (from 1 to S). Your function should compute the new membrane voltage V(t+Δt) based on the previous voltage V(t) and the current conductances g_i(t_rel), where t_rel is the time relative to the most recent spike. (Depending on the current, this might be the most recent theta spike, gamma spike, or the cell's own spike.) Start with a very simple cell that just has a leak current.

Write the first version of the main loop of your simulation. It should progress through all the time steps, recalculating the membrane voltage of each pyramidal cell at each step. Set the cell's initial membrane voltage to something other than the resting potential of -60 mV. When the main loop finishes, plot the membrane voltage history and verify that the cell settled to its resting potential.

Theta modulation from the medial septum is simulated by a series of theta "spikes"; each spike triggers an inhibitory conductance. Create an array thetaSpikes of size S containing, for each entry, the time of the most recent theta spike. (At a theta frequency of 8 Hz, the last theta spike time should stay the same for 125 msec, then jump ahead by 125 msec., etc.)

Extend your updatePyramid function to include the theta current. Rerun the simulation and verify that theta ipsp's are present.

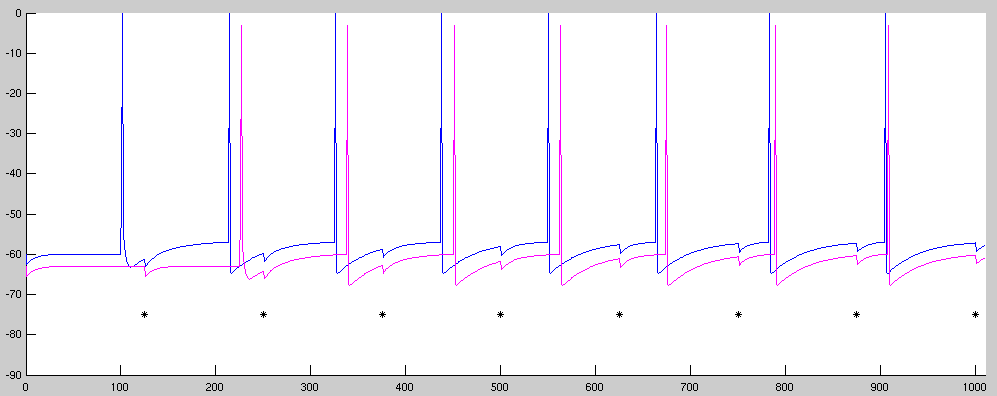
In the example plot above, created with P=2 (two pyramidal cells) and an S value of around 510, the black asterisks mark theta cell spikes. You can see that each theta spike briefly hyperpolarizes the pyramidal cells due to the inhibitory conductance. The two pyramidal cells have identical membrane voltages, but the traces are offset vertically in the plot so that they won't be right on top of each other.

Fourth Step

Now we need to make the neurons spike. Create a P×S array called inputSpikes that contains the last spike time of an input to each of the P pyramidal cells. These spikes will control an "input" current whose parameters are not listed in Table 1, but you can find them on p. 3 of the "Reverse and Forward Buffering" paper; use 0 mV as the reversal potential.

Modify the updatePyramid function to include the AHP, ADP, and input currents, and add logic to make the cell spike if the membrane voltage goes above threshold. When the cell enters the "spiking" state it should hold its membrane voltage at 0 mV for 1 millisecond; then it should enter a refractory state for 2 milliseconds where it refuses to spike no matter what the membrane voltage is. When the refractory period is over, the cell should return to its normal state and can spike again if the membrane voltage goes above threshold.

Write a function setInput(p,ts) that sets up an input spike for pyramidal cell number p at time ts by writing appropriate values into the inputSpikes array. You call this function at the beginning of your simulation for each input spike you want to apply. Note that since inputSpikes(p,i) encodes the time of the last spike up to and including step i of the simulation, when you add a spike to the array you must modify all the succeeding entries on that row.

Set up an input spike for the first pyramidal cell at time t=100, and run your simulation with two cells. Verify that the first cell fires repeatedly while the second one remains inactive, but both cells show theta ipsps. Note: you must set the firing rate threshold to -57 mV rather than the -50 mV value given in the paper.

Now set up an input to the second pyramidal cell at time t=225. Run the simulation again. Notice that the relative spike times of the two pyramidal cells are not stable. We will fix this in the next step.

Fifth Step

The inhibitory gamma interneuron prevents pyramidal cells encoding different items from firing at the same time. As soon as one pyramidal cell fires, the interneuron supplies brief inhibition to all the pyramidal cells, which will delay any cell that was just about to fire.

To implement the gamma interneuron you will need to create a variable gammaNeuron containing the same kind of structure as a pyramidal cell. (There is only one of these interneurons in the simulation so you don't need an array of them.) This neuron should receive excitatory input from the pyramidal cells, which you can model as a single input current using the last spike time of the most recently-fired pyramidal cell.

Write an updateGamma function to update the state of the gamma interneuron, using the appropriate parameters for that neuron instead of the ones for the pyramidal cell.

Modify your updatePyramid function to include inhibitory input from the gamma interneuron. Modify your display code to display the gamma interneuron's firing.

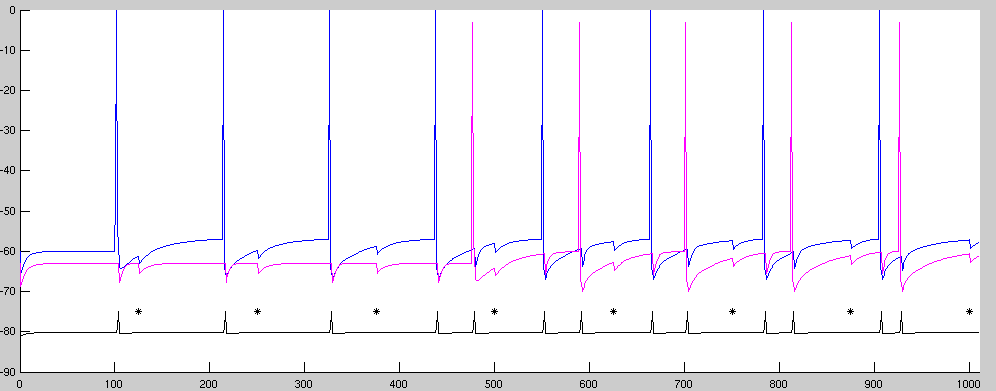
In the above plot, the black asterisks mark theta cell spikes, and the membrane voltage of the gamma cell is shown as a black line. The first input is at t=100 msec and the second at t=475 msec. The gamma cell trace is scaled and translated downward to get it out of the way of the pyramidal cell voltage traces.

Run your simulation with four pyramidal cells for 1510 time steps. Input should come at t=100 for the first cell, t=225 for the second, t=355 for the third, and t=605 for the fourth. Verify that the relative spike times are stable.

Sixth Step

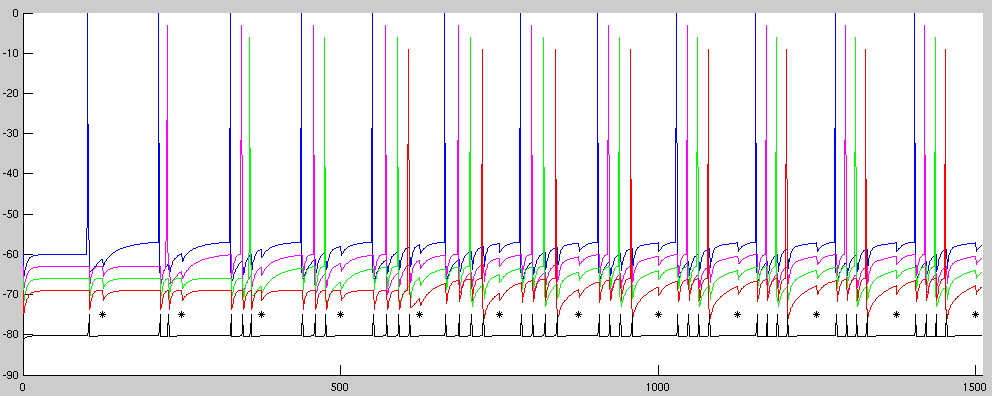
Write a function spikestats that is called after the simulation has run, and prints out the following statistics separately for each pyramidal cell:

Time of each spike
Inter-spike interval for each spike, i.e., the time between this spike and the previous one
Phase of each spike relative to the theta cycle

We're applying external inputs late in the theta cycle. If your simulation is functioning properly you will see that with repeated spiking the phase of the most recently added input advances, but the phase of the earliest memory item cannot advance too far due to theta inhibition, and the phases of the remaining items cannot advance too far due to gamma inhibition resulting from the firing of preceding items in the buffer.

What to Hand In

Email a zip file containing the following:

The answers to the questions posed in the text above.
Plots of your conductance functions.
A screen capture of the plot your simulation produces.
The output of the spikestats function.
Your MATLAB code.

Check the class schedule for the due date on your project.

Last-Minute Notes

See this suggestion about global variables.
In order for gamma inhibition to work correctly you must have the correct value of anorm. Also, for the gamma current, the G parameter must be increased from 100 to 150.
The conductance parameters given here were tuned for Δt = 1 msec. To use a finer-scale Δt value, which would reduce quantization error, the conductances would have to be tweaked a bit. You're not being asked to do that.
The table of parameters in the paper shows the leak conductance as 111, but the text says that g_leak = C/τ_leak, which might lead you to infer that the value should be 1/9 = 0.111. They messed up on the units. The 111 value is correct. In general, don't worry about getting the units right; just use the numbers in Table 1.
Be sure to use a 2 millisecond refractory period.

Dave Touretzky