Ruppert's Delaunay Refinement Algorithm

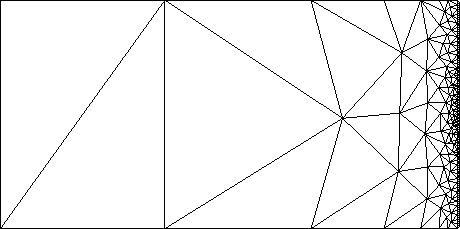
Ruppert's algorithm for two-dimensional quality mesh generation [15] is perhaps the first theoretically guaranteed meshing algorithm to be truly satisfactory in practice. It produces meshes with no small angles, using relatively few triangles (though the density of triangles can be increased under user control) and allowing the density of triangles to vary quickly over short distances, as illustrated in Figure 4. (Chew [3] independently developed a similar algorithm.) This section describes Ruppert's Delaunay refinement algorithm as it is implemented in Triangle.

Triangle's input is a planar straight line graph (PSLG), defined to be a collection of vertices and segments (where the endpoints of every segment are included in the list of vertices). Figure 5 illustrates a PSLG defining an electric guitar. Although the definition of ``PSLG'' normally disallows segment intersections (except at segment endpoints), Triangle can detect segment intersections and insert vertices.

   

Figure 4: A demonstration of the ability of the Delaunay refinement algorithm to achieve large gradations in triangle size while constraining angles. No angles are smaller than 24^o.

   

Figure 5: Electric guitar PSLG.

   

Figure 6: Delaunay triangulation of vertices of PSLG. The triangulation does not conform to all of the input segments.

   

Figure 7: Constrained Delaunay triangulation of PSLG.

   

Figure 8: Triangles are removed from concavities and holes.

   

Figure 9: Conforming Delaunay triangulation with 20^o minimum angle.

The first stage of the algorithm is to find the Delaunay triangulation of the input vertices, as in Figure 6. In general, some of the input segments are missing from the triangulation; the second stage is to insert them. Triangle can force the mesh to conform to the segments in one of two ways, selectable by the user. The first is to insert a new vertex corresponding to the midpoint of any segment that does not appear in the mesh, and use Lawson's incremental insertion algorithm to maintain the Delaunay property. The effect is to split the segment in half, and the two resulting subsegments may appear in the mesh. If not, the procedure is repeated recursively until the original segment is represented by a linear sequence of constrained edges in the mesh.

The second choice is to simply use a constrained Delaunay triangulation (Figure 7). Each segment is inserted by deleting the triangles it overlaps, and retriangulating the regions on each side of the segment. No new vertices are inserted. For reasons explained in Section 3.1, Triangle uses the constrained Delaunay triangulation by default.

The third stage of the algorithm, which diverges from Ruppert [15], is to remove triangles from concavities and holes (Figure 8). A hole is simply a user-specified point in the plane where a ``triangle-eating virus'' is planted and spread by depth-first search until its advance is halted by segments. (This simple mechanism saves both the user and the implementation from a common outlook wherein one must define oriented curves whose insides are clearly distinguishable from their outsides. Triangle's method makes it easier to treat holes and internal boundaries in a unified manner.) Concavities are recognized from unconstrained edges on the boundary of the mesh, and the same virus is used to hollow them out.

The fourth stage, and the heart of the algorithm, refines the mesh by inserting additional vertices into the mesh (using Lawson's algorithm to maintain the Delaunay property) until all constraints on minimum angle and maximum triangle area are met (Figure 9). Vertex insertion is governed by two rules.

• The diametral circle of a segment is the (unique) smallest circle that contains the segment. A segment is said to be encroached if a point lies within its diametral circle. Any encroached segment that arises is immediately split by inserting a vertex at its midpoint. The two resulting subsegments have smaller diametral circles, and may or may not be encroached themselves. See Figure 10.

     

  
  Figure 10: Segments are split recursively (while maintaining the Delaunay property) until no segments are encroached.
  

     

  
  Figure 11: Each bad triangle is split by inserting a vertex at its circumcenter and maintaining the Delaunay property.
  

• The circumcircle of a triangle is the unique circle that passes through all three vertices of the triangle. A triangle is said to be bad if it has an angle too small or an area too large to satisfy the user's constraints. A bad triangle is split by inserting a vertex at its circumcenter (the center of its circumcircle); the Delaunay property guarantees that the triangle is eliminated (see Figure 11). If the new vertex encroaches upon any segment, the vertex is deleted (reversing the insertion process) and all the segments it encroached upon are split.

Encroached segments are given priority over bad triangles. A queue of encroached segments and a queue of bad triangles are initialized at the beginning of the refinement stage and maintained throughout; every vertex insertion may add new members to either queue. The former queue rarely contains more than one segment except at the beginning of the refinement stage, when it may contain many.

   

Figure 12: Demonstration of the refinement stage. The first two images are the input PSLG and its constrained Delaunay triangulation. In each image, highlighted segments or triangles are about to be split, and highlighted vertices are about to be deleted. Note that the algorithm easily accommodates internal boundaries and holes.

The refinement stage is illustrated in Figure 12. Ruppert [15] proves that this procedure halts for an angle constraint of up to 20.7^o. In practice, the algorithm generally halts with an angle constraint of 33.8^o, but often fails to terminate given an angle constraint of 33.9^o. It would be interesting to discover why the cutoff falls there.

• Selected Implementation Issues
• A Negative Result on Quality Triangulations