Homework 5 (Due Sat 1-OCT at 8pm)

Important Notes:

Read the "Important Notes" at the top of hw1. The same general rules apply to all homework unless otherwise specified.
This homework is solo. You must not collaborate with anyone (besides current course TA's and faculty) in any way. See the syllabus for more details.
You will need these starter files:
For this hw, you may submit up to 6 times, but only your last submission counts.
Do not use recursion this week, or any imports/data structures we have not yet covered.
Do not hardcode the test cases in your solutions.
As always, all your functions must be non-destructive unless the problem specifically indicates otherwise.
Also, if Python happens to provide a function that basically outright solves a problem do not use that function. Naturally, we are looking for you to write the core logic of the problem.

removeRowAndCol (non-destructive and destructive) [10 pts; 5 pts each]
Here we will write removeRowAndCol twice -- once non-destructively, and then again destructively. Note that neither of these versions may call nor essentially duplicate the other version. So in particular, your nondestructive version may not do this:
```
    L = copy.deepcopy(L)
    doDestructiveVersion(L)
    return L
```
Instead, do not use copy.deepcopy and directly construct the modified 2d list.

Both functions take a rectangular list L and two ints, row and col. In both cases, the goal is to obtain a version of the list that has the given row and given column removed. You may assume that row and col are both legal values (that is, they are non-negative integers that are smaller than the number of rows and columns, respectively). For example, the list shown to the left would lead to the result shown on the right when called with the row 1 and the column 2.
list result
[ [ 2, 3, 4, 5], [ 8, 7, 6, 5], [ 0, 1, 2, 3] ]
[ [ 2, 3, 5], [ 0, 1, 3] ]
nondestructiveRemoveRowAndCol(L, row, col): the non-destructive version should return a new list, and should not modify the provided list at all.

destructiveRemoveRowAndCol(L, row, col): the destructive version should modify the original list, and should return None.

isKingsTour(board) [15 pts]
Background: in Chess, a King can move from any square to any adjacent square in any of the 8 possible directions. A King's Tour is a series of legal King moves so that every square is visited exactly once.

For example, here is a valid Kings Tour: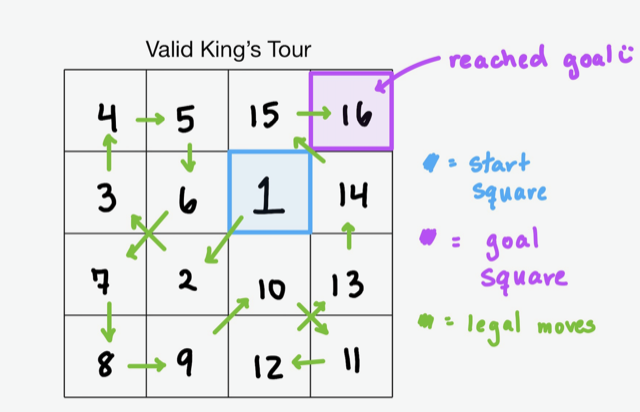

And here is an invalid Kings Tour: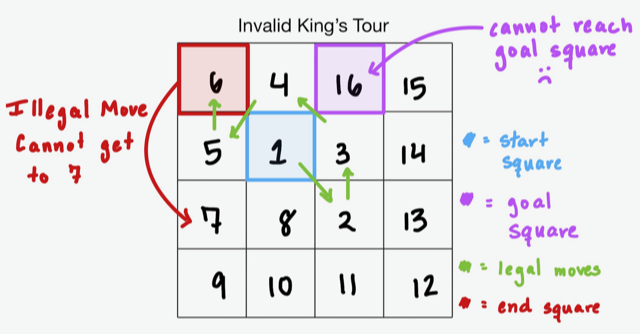

We can represent a Kings Tour in a 2d list where the numbers represent the order the squares are visited, going from 1 to N². For example, consider these 2d lists:
```
   [ [  3, 2, 1 ],        [ [  1, 2, 3 ],      [ [ 3, 2, 1 ],
     [  6, 4, 9 ],          [  7, 4, 8 ],        [ 6, 4, 0 ],
     [  5, 7, 8 ] ]         [  6, 5, 9 ] ]       [ 5, 7, 8 ] ]
```
The first is a legal Kings Tour but the second is not, because there is no way to legally move from the 7 to the 8, and the third is not, because it contains a 0 which is out of range. Also, this should work not just for 3x3 boards but for any NxN board. For example, here is a legal Kings Tour in a 4x4 board:
```
    [ [  1, 14, 15, 16],
      [ 13,  2,  7,  6],
      [ 12,  8,  3,  5],
      [ 11, 10,  9,  4]
    ]
```
With this in mind, write the function isKingsTour(board) that takes a 2d list of integers, which you may assume is NxN for some N>0, and returns True if it represents a legal Kings Tour and False otherwise.

isMagicSquare(L) [15 pts]
Write the function isMagicSquare(L) that takes an arbitrary list (that is, a possibly-empty, possibly-ragged, possibly-2d list of arbitrary values) and returns True if it is a magic square and False otherwise, where a magic square has these properties:
1. The list is 2d, non-empty, square, and contains only integers, where no integer occurs more than once in the square.
2. Each row, each column, and each of the 2 diagonals each sum to the same total. Note that we are not requiring that the integers are strictly in the range from 1 to n for some n. We are just requiring that the integers are unique and that the sums are all the same.
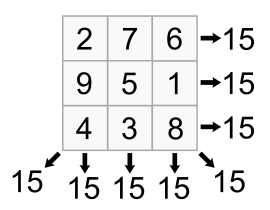
If you are curious, you can optionally see here for more details, including this sample magic square:

wordSearchWithIntegerWildCards(board, word) [20 pts]
Here we will modify wordSearch so that we can include positive integers in the board, like so (see board[1][1]):
```
    board = [ [ 'p', 'i', 'g' ],
              [ 's',   2, 'c' ],
            ]
```
When matching a word, a positive integer on the board matches exactly that many letters in the word. So the board above contains the word "cow" starting from [1,2] heading left, since the 2 matches "ow". It also contains the word "cows" for the same reason. To make this work, of the three functions in our wordSearch solution, the outer two do not have to change (except a slight renaming), but the innermost one does. Add all three functions to your hw file, renaming the outermost function to wordSearchWithIntegerWildCards, and then rewrite the innermost function here so that it works as described.

Medical Image Volume Viewer! [40 pts]

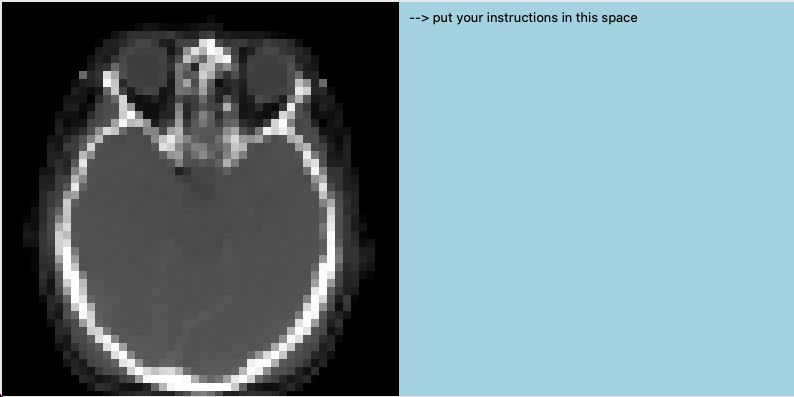
In this problem, you will build an image viewer application that interactively creates a number of different 2D views of a 3D medical imaging volume. We'll load the medical imaging volume for you into a 3D list of integers. From there, your viewer will extract either a 2D slice or a 2D MIP image (maximum intensity projection, see below) from the volume, and we'll display it on the cmu_112_graphics canvas. Users will also be able to pan your image (shift the image left, right, up, and down) using controller events that you will design.

Here's a quick video, showing you what your viewer should be able to do when you are finished!

Whoa, that sounds like a lot, but don't worry, we'll break it down in to four parts: panImage, volSlicer, maximumIntensityProjection, and finally the viewer application. The first three parts will be checked by the autograder, so you should be able to confidently use those functions in the final viewer application step.

panImage(im, dx, dy, backgroundValue) [10 pts]

Background: a 2D image is rectangular grid of size numColumns x numRows, where each location in the grid is called a pixel and that pixel contains a value. In this assignment, the pixel values will just be integers, but you could also have RGB color values stored in each pixel. Write the function panImage(im, dx, dy, backgroundValue) that takes an input image (a rectangular 2d list) and returns a new 2d list that contains the values from the input image but shifted horizontally by dx pixels or vertically by dy pixels.
im panImage(im, -2, 0, 88)
[ [ 10, 11, 12, 13], [ 14, 15, 16, 17], [ 18, 19, 20, 21] ]
[ [ 12, 13, 88, 88], [ 16, 17, 88, 88], [ 20, 21, 88, 88] ]
The output image (a 2d list) should have the exact same dimensions as the input 2d list. Some pixels in the output image will not have a corresponding location in the input image (because we shifted the image); these pixels should be filled with the given backgroundValue parameter.

Easy to mess up: a positive value for dx should shift the input image to the right, leading to backgroundValues to appear in leftmost column(s) of the output image. Conversely, negative values for dx should shift the input image to the left.

Similarly, positive values for dy should shift the input image down, leading to backgroundValues to appear in the topmost row(s) of the output image.

Your function should accept any integer values of dx and dy without crashing. If the input image is shifted completely off of the original location, then the resulting output image should be filled with all backgroundValues.

volSlicer(vol, sliceIndex, sliceAxis) [10 pts]

Note: here we are using the term "slice" as a slice through a 3D volume, which is somewhat related to but slightly different than the Python term for slice/slicing.

Background: a 3D image volume is 3D rectangular grid of size numSlices x numColumns x numRows, where each location in the grid is called a voxel (volume pixel) and that voxel contains a value. We'll store these volumes as rectangular 3D lists. Note: In this assignment, the pixel values will just be integers.

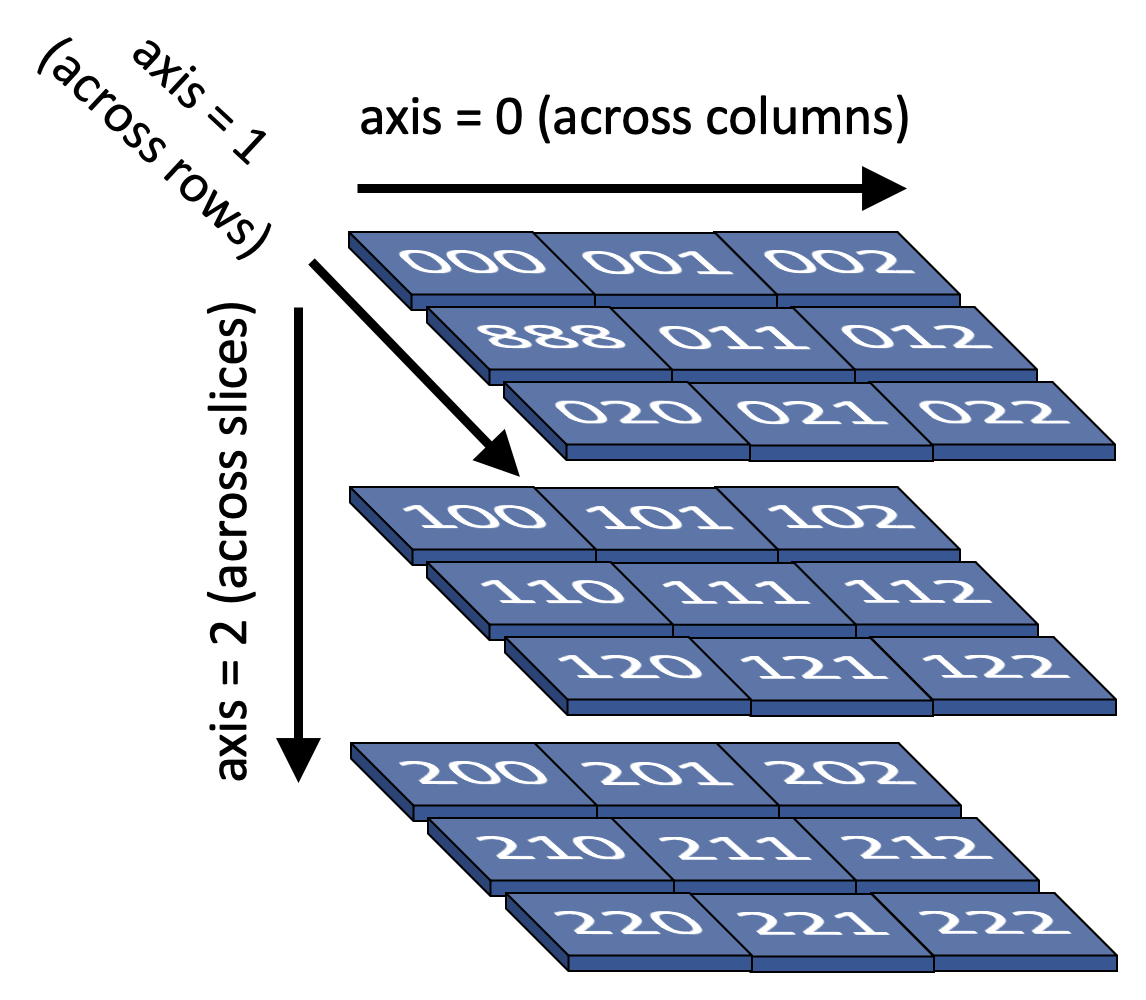
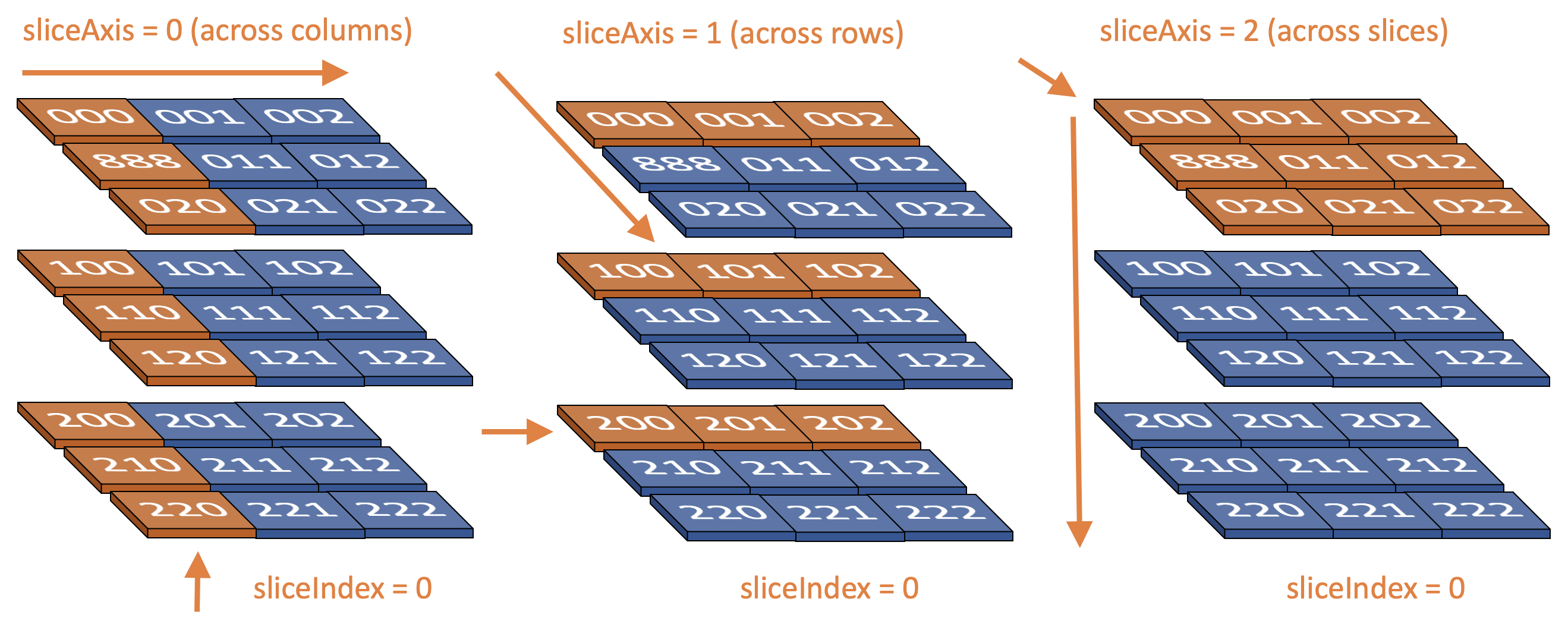
Write the function volSlicer(vol, sliceIndex, sliceAxis) that takes an input volume (a rectangular 3d list) and returns an output image (a new 2d list) that contains the values corresponding to one perpendicular slice through the volume. The specific slice through the volume will depend on two parameters sliceIndex and sliceAxis. The slice axis will be one of three values, 0, 1, 2, that will indicate along which axis of the volume we are slicing and the sliceIndex will be the index location along that axes. This is probably best illustrated with a few examples. Note that for illustrative purposes, we are putting strings in the examples below rather than integers. Changing the sliceAxis example using the volume above:

Changing the sliceIndex example using the volume above:

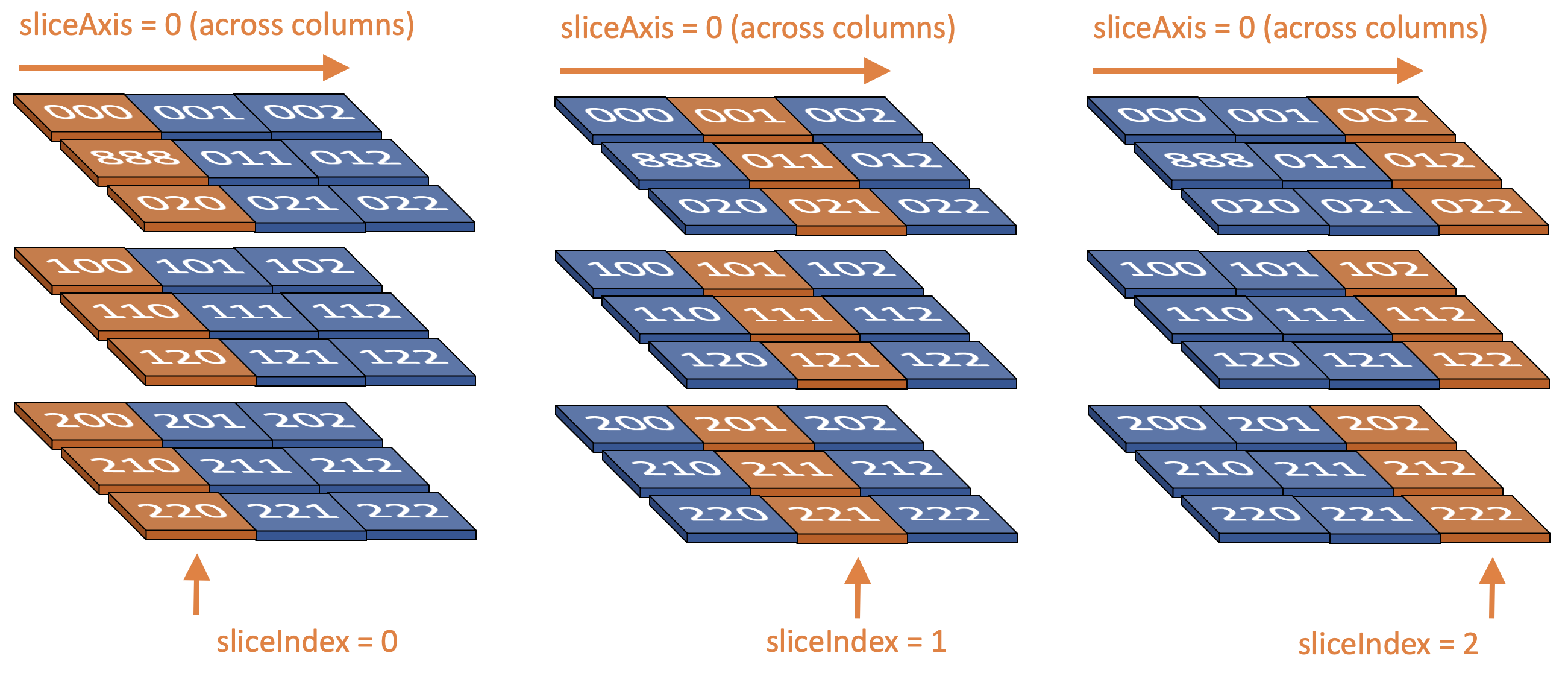
There are even more examples in the test cases for volSlicer().

Note: You may assume that you are given valid integer values for sliceIndex and sliceAxis. Note: It is ok to write three different code blocks to handle the three different sliceAxis settings.

maximumIntensityProjection(vol, maxAxis) [10 pts]

Write the function maximumIntensityProjection(vol, maxAxis) that takes an input volume (a rectangular 3d list) and returns an output image (a new 2d list) that contains the values corresponding to the maximum value found when looking at the volume along the maxAxis. maxAxis essentially has the same meaning as sliceAxis in volSlicer.

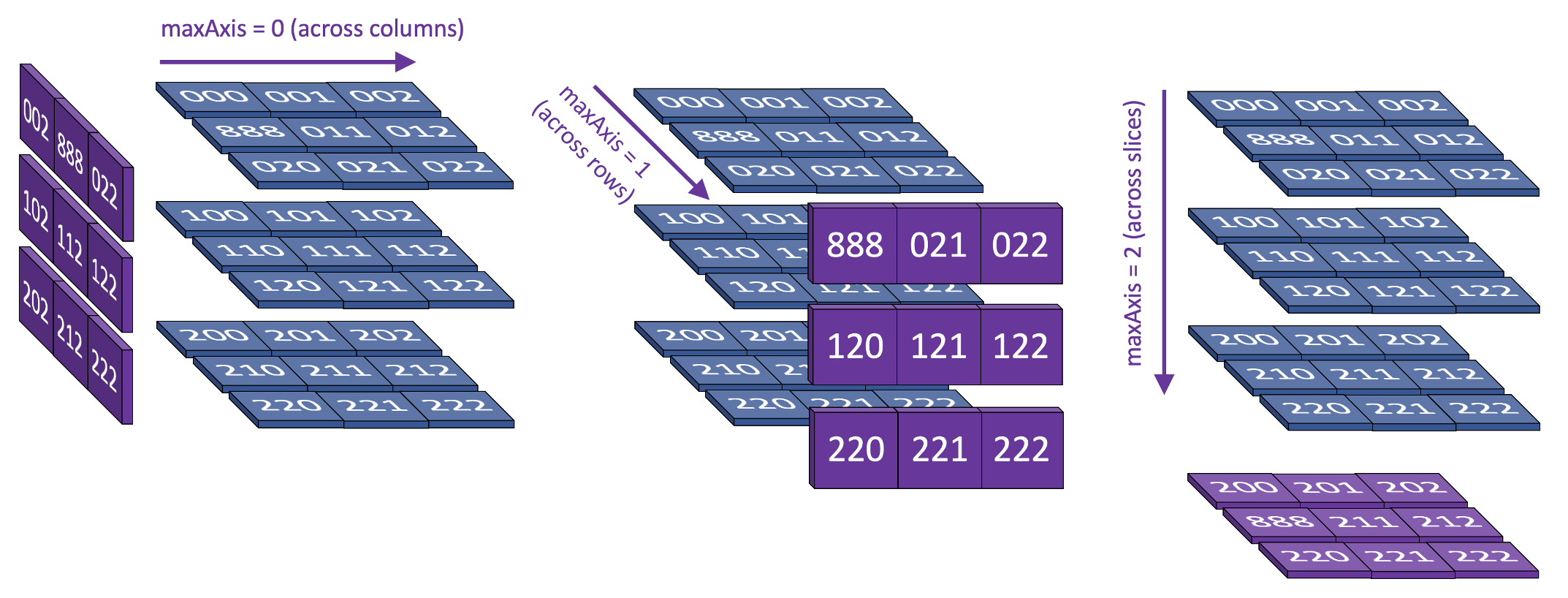
Note: You may assume that you are given valid integer values for maxAxis. Note: It is ok to write three different code blocks to handle the three different maxAxis settings.

Viewer application with cmu_112_graphics [10 pts]

Now we can put all of the pieces together in a medical image viewer applications. The viewer will load the head_ct_50_50_50.csv 50x50x50 volume containing CT scan data from the Visible Human Project. Your job will be to implement the following features in the viewer application:
- Change between all three slice axes
- Increment and decrement the slice index (across all possible indices)
- Change between slice mode and MIP (maximum intensity projection) mode
- Pan the slice or MIP image up, down, left, and right
- Display instructions in the right-hand side to tell the user how to use all of the above features
- Don't crash. The application should not crash/error when the user is interacting with the viewer controls
- Don't violate the model-view-controller paradigm
You get to choose which cmu_112_graphics controllers change which features.
See the starter code for more instructions on where you need to implement your functionality.
Bonus/Optional: makeWordSearch(wordList, replaceEmpties) [2.5 pts]
Write the function makeWordSearch(wordList, replaceEmpties) that takes a possibly-empty list of non-empty lowercase words and a boolean value replaceEmpties (that we will explain later) and returns a wordSearch (a 2d list of lowercase letters) that contains all the given words, according to the algorithm described here.

To start, if the wordList is empty, just return None. Otherwise, start with a 0x0 board. Add each word in the order given to the board according to the rules below, and return the resulting board.

First, if the word is longer than the number of rows in the board (which is guaranteed to happen on the first word), then it cannot possibly fit on the board (right?). In that case, add empty rows and empty columns to the board, keeping the board square, so that the number of rows equals the length of the word. Note that empty cells do not yet contain any letters.

Next, if possible, add the word in the location and direction resulting in the lowest cost, where the cost is the total number of empty cells that must be filled in with a letter to add the word at the given location and direction. If there is a tie, use the first location and direction with the lowest cost, where you should sweep across row0 from left-to-right, then row1, and so on, and where the directions should be ordered in the same way (up-left, up, up-right, left, right, down-left, down, down-right).

It is possible that this process completes with no place to add the word. In that case, add one more row and one more column of empty cells to the board, keeping it square, and then add the word to the bottom row starting at column 0 and heading to the right.

Hint: you should carefully re-read the previous paragraph, as it may not be too intuitive!

After you have added all the words, if the replaceEmpties parameter is False, return the board as-is, with empty cells containing a dash ('-'). However, if replaceEmpties is True, then for each empty cell on the board, replace it with the first lowercase letter that does not appear among its non-empty neighbors. Do this sweeping the usual way, left-to-right across row0, then row1, and so on.

You will surely want to add some well-chosen helper functions here. Also, you may wish to carefully review a few test cases we are providing you, prior to designing your solution:
def testMakeWordSearch(): print("Testing makeWordSearch()...", end="") board = makeWordSearch([], False) assert(board == None) board = makeWordSearch(["ab"], False) assert(board == [['a', 'b'], ['-', '-'] ]) board = makeWordSearch(["ab"], True) assert(board == [['a', 'b'], ['c', 'd'] ]) board = makeWordSearch(["ab", "bc", "cd"], False) assert(board == [['a', 'b'], ['c', 'd'] ]) board = makeWordSearch(["ab", "bc", "cd", "de"], False) assert(board == [['a', 'b', '-'], ['c', 'd', '-'], ['d', 'e', '-']]) board = makeWordSearch(["ab", "bc", "cd", "de"], True) assert(board == [['a', 'b', 'a'], ['c', 'd', 'c'], ['d', 'e', 'a']]) board = makeWordSearch(["abc"], False) assert(board == [['a', 'b', 'c'], ['-', '-', '-'], ['-', '-', '-']]) board = makeWordSearch(["abc"], True) assert(board == [['a', 'b', 'c'], ['c', 'd', 'a'], ['a', 'b', 'c']]) board = makeWordSearch(["abc", "adc", "bd", "bef", "gfc"], False) assert(board == [['a', 'b', 'c'], ['d', 'e', '-'], ['c', 'f', 'g']]) board = makeWordSearch(["abc", "adc", "bd", "bef", "gfc"], True) assert(board == [['a', 'b', 'c'], ['d', 'e', 'a'], ['c', 'f', 'g']]) print("Passed!")

list		result
[ [ 2, 3, 4, 5], [ 8, 7, 6, 5], [ 0, 1, 2, 3] ]		[ [ 2, 3, 5], [ 0, 1, 3] ]

im		panImage(im, -2, 0, 88)
[ [ 10, 11, 12, 13], [ 14, 15, 16, 17], [ 18, 19, 20, 21] ]		[ [ 12, 13, 88, 88], [ 16, 17, 88, 88], [ 20, 21, 88, 88] ]