My current research deals with approximate solutions for tightly coupled partially observable stochastic games with common payoffs.

Partially Observable Markov decision processes (POMDPs) are a rich framework for modelling uncertainty in robot control problems. Unlike Markov decision processes (MDPs), however, they cannot be directly applied to muli-robot problems, even when a robot team has a common reward structure, unless that team also has unlimited, instantaneous communication. Instead, game theory must be used to model how each member of the team will make individual decision about what actions to take given its own observation histories and a model of its teammates. I model control problems in this domain as partially observable stochastic games (POSGs).

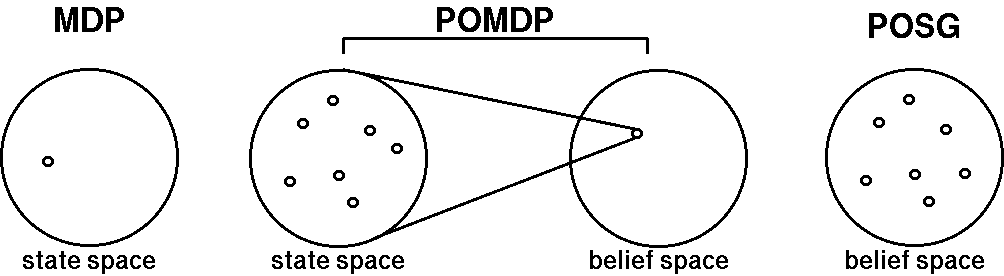
The following figure perhaps best explains why each robot cannot model the problem as a POMDP. In the single robot case, a POMDP transforms uncertainty over a set of states into a single point in belief space and MDP-planning can then be performed in that new space. In a POSG, however, uncertainty still remains over a set of points in belief space. This is because while each robot knows its own history of observations and actions, it does not know those of its teammates with certainty and therefore has to maintain a probability distribution over the possible joint state of the team.

Solving a POSG is intractable for all but extremely small problems with limited finite horizon. I am interested in approximating the optimal solution to a POSG by using an approach that interleaves planning and execution. In my algorithm, robots find a one-step policy at each timestep and use the policies from earlier timesteps and common observations to prune down the number of different joint histories of observations and actions that must be tracked.

This approach has been applied successful to robot tag problems in both simulation and on real robots. For example, this animated gif shows the paths taken by a robot team searching for an opponent in the A-wing of Gates Hall.