Networks derived from hypercubes form the architectural basis of most
parallel computers, including machines such as the BBN Butterfly, the
Connection Machine, the IBM RP3 and GF11, the Intel iPSC, and the NCUBE.
The butterfly, in particular, is quite popular, and has been
demonstrated to perform reasonably well in practice. An example of an
8-input butterfly is illustrated in Figure 1. The
nodes in this graph represent switches, and the edges represent wires.
Each node in the network has a distinct label 
, where r is
the row, and l is the level. In a butterfly with N inputs, the
row is a 
-bit binary number
and the level is an integer between 0
and 
. The nodes on level 0 and 
are called the
inputs and outputs, respectively. For 
, a node
labeled 
is connected to nodes 
and 
, where
denotes r with bit l complemented (bit 0 is the most
significant, bit 
the least).
The primary duty of the network in a parallel machine is to route
messages between its processors and/or memory modules. In a
butterfly, messages are typically sent from the switches on level 0,
called the inputs, to those on level 
, called the
outputs. In a one-to-one routing problem, each input is the
origin of at most one message, and each output is the destination of a
most one message. One-to-one routing is also called permutation
routing. All of the algorithms discussed in this paper route
messages in a store-and-forward fashion. A store-and-forward
algorithm treats messages as indivisible objects. At each step, a
message can either remain at a switch or move in its entirety from one
switch to another across an edge, provided that no other messages use
the same edge at that step. Store-and-forward routing is also called
packet switching, and messages are often referred to as packets.
A related paper [2] extends the results of this paper for
a different method of routing called circuit switching.
One of the nice features of the butterfly is that there is a simple
algorithm for finding a path of length 
from any input to any
output. Upon reaching switch 
, 
, a packet with
destination 
compares r with R. If they are
equal, the packet takes the edge to 
. If not, it takes the
edge to 
. One problem with the butterfly is that this path
is unique. As a consequence, if some switch or edge along the unique
path from input i to output j (say) becomes congested or fails,
then communication between input i and output j will be disrupted.
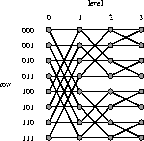
Figure 1: An 8-input butterfly network.