In this paper, we are primarily concerned with randomly-wired splitter networks. A randomly-wired splitter network is a splitter network where the up and down edges within each splitter are chosen at random subject to the constraint that each splitter input is incident to d up and d down edges, and each splitter output is incident to 2d incoming edges.
The crucial property that randomly-wired splitter networks are likely
to possess is known as expansion. In particular, an M-input
splitter is said to have 
-expansion if every set of 
inputs is connected to at least 
up outputs
and 
down outputs, where 
and 
are
fixed constants. For example, see Figure 4.
A splitter network is said to have 
-expansion
if all of its splitters have 
-expansion. More simply,
a splitter or a splitter network is said to have expansion if
it has 
-expansion for some constants 
and
. A splitter network with expansion is more commonly known
as a multibutterfly [29], and a multibutterfly
with 
-expansion and multiplicity d consists of
splitters in which each splitter input is incident to d up and d
down edges and for which any 
splitter inputs are
adjacent to 
splitter outputs.
Splitters with expansion are known to exist for any 
, and
they can be constructed deterministically in polynomial time
[11, 23, 29], but randomized wirings typically
provide the best possible expansion. In fact, the expansion of a
randomly-wired splitter will be close to d-1 with probability close
to 1, provided that 
is a sufficiently small constant. (For
a discussion of the tradeoffs between 
and 
in
randomly-wired splitters, see [20, 29].)
A multibutterfly with 
-expansion is good at routing
because one must block 
splitter outputs in order to block
k splitter inputs. In classical networks such as the butterfly, the
reverse is true: it is possible to block 2k inputs by blocking only
k outputs. When this effect is compounded over several levels, the
effect is dramatic. In a butterfly, a single fault can block 
switches l levels back, whereas in a multibutterfly, it takes
faults to block a single switch l levels back.
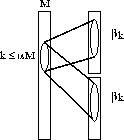
Figure 4: An M-input splitter with 
-expansion.
In 1989, Upfal showed that any N-input multibutterfly can route any
one-to-one problem in 
steps using a simple greedy
algorithm [29], and that, by using pipelining, any N-input
multibutterfly can route 
one-to-one problems in 
steps. Although the proof is complicated and the constants hidden
by the Big Oh notation are large, the result is important because the
only previously known deterministic on-line linear-hardware 
-step packet routing algorithm [18] requires the use
of the AKS sorting circuit [1] (which is even more
complicated and has even larger constant factors).