


Next: A Generalization of AIS-BN:
Up: AIS-BN: Adaptive Importance Sampling
Previous: Heuristic Initialization in AIS-BN
There are several tunable parameters in the AIS-BN algorithm. We
base the choice of these parameters on the Central Limit Theorem
(CLT). According to CLT, if Z1, Z2, ..., Zn are
independent and identically distributed random variables with
E(Zi) =  and Var
(Zi) =
and Var
(Zi) =  , i = 1, ...,
n, then
, i = 1, ...,
n, then
 = (Z1 + ... + Zn)/n is approximately
normally distributed when n is sufficiently large. Thus,
= (Z1 + ... + Zn)/n is approximately
normally distributed when n is sufficiently large. Thus,
 P( P(   . t) = . t) =   e-x2/2dx . e-x2/2dx .
|
(11) |
Although this approximation holds when n approaches infinity,
CLT is known to be very robust and lead to excellent
approximations even for small n. The formula of
Equation 11 is an (
 ,
,  ) Relative Approximation, which is an estimate
) Relative Approximation, which is an estimate
 of
of  that satisfies
If
that satisfies
If  has been fixed,
where
has been fixed,
where
 (z) =
(z) = 
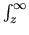 e-x2/2dx.
Since in our sampling problem,
e-x2/2dx.
Since in our sampling problem,  (corresponding to
Pr(
(corresponding to
Pr( ) in Figure 2) has been fixed, setting
) in Figure 2) has been fixed, setting
 to a smaller value amounts to letting
to a smaller value amounts to letting
 /
/ be smaller. So, we can adjust the parameters
based on
be smaller. So, we can adjust the parameters
based on
 /
/ , which can be estimated using
Equation 3. It is also the theoretical intuition
behind our recommendation
wk
, which can be estimated using
Equation 3. It is also the theoretical intuition
behind our recommendation
wk  1/
1/ in
Section 3.1. While we expect that this should work well
in most networks, no guarantees can be given here -- there exist
always some extreme cases in sampling algorithms in which no good
estimate of variance can be obtained.
in
Section 3.1. While we expect that this should work well
in most networks, no guarantees can be given here -- there exist
always some extreme cases in sampling algorithms in which no good
estimate of variance can be obtained.



Next: A Generalization of AIS-BN:
Up: AIS-BN: Adaptive Importance Sampling
Previous: Heuristic Initialization in AIS-BN
Jian Cheng
2000-10-01
![]() and Var
(Zi) =
and Var
(Zi) = ![]() , i = 1, ...,
n, then
, i = 1, ...,
n, then
![]() = (Z1 + ... + Zn)/n is approximately
normally distributed when n is sufficiently large. Thus,
= (Z1 + ... + Zn)/n is approximately
normally distributed when n is sufficiently large. Thus,

 .
.