next up previous
Next: A Generic Importance Sampling Up: Importance Sampling Algorithms for Previous: Importance Sampling Algorithms for


Mathematical Foundations

Let g($ \bf X$) be a function of m variables $ \bf X$ = (X1,..., Xm) over a domain $ \Omega$ $ \subset$ Rm, such that computing g($ \bf X$) for any $ \bf X$ is feasible. Consider the problem of approximate computation of the integral

I = $\displaystyle \int_{\Omega}^{}$g($\displaystyle \bf X$) d$\displaystyle \bf X$  . (1)

Importance sampling approaches this problem by writing the integral (1) as

I = $\displaystyle \int_{\Omega}^{}$$\displaystyle {\frac{g({\bf X})}{f({\bf X})}}$ f ($\displaystyle \bf X$) d$\displaystyle \bf X$  ,

where f ($ \bf X$), often referred to as the importance function, is a probability density function over $ \Omega$. f ($ \bf X$) can be used in importance sampling if there exists an algorithm for generating samples from f ($ \bf X$) and if the importance function is zero only when the original function is zero, i.e., g($ \bf X$) $ \neq$ 0   $ \Longrightarrow$  f ($ \bf X$) $ \neq$ 0.

After we have independently sampled n points $ \bf s_{1}^{}$, $ \bf s_{2}^{}$, ..., $ \bf s_{n}^{}$, $ \bf s_{i}^{}$ $ \in$ $ \Omega$, according to the probability density function f ($ \bf X$), we can estimate the integral I by

$\displaystyle \hat{I}_{n}^{}$ = $\displaystyle {\frac{1}{n}}$$\displaystyle \sum\limits_{i=1}^{n}$$\displaystyle {\frac{g({\bf s}_i)}{f({\bf s}_i)}}$ (2)

and estimate the variance of $ \hat{I}_{n}^{}$ by

$\displaystyle \widehat{\sigma }^{2}_{}$($\displaystyle \hat{I}_{n}^{}$) = $\displaystyle {\frac{1}{n\cdot(n-1)}}$$\displaystyle \sum\limits_{i=1}^{n}$$\displaystyle \left(\vphantom{\frac{g({\bf s}_i)}{f({\bf s}_i)}-\hat I_n}\right.$$\displaystyle {\frac{g({\bf s}_i)}{f({\bf s}_i)}}$ - $\displaystyle \hat{I}_{n}^{}$$\displaystyle \left.\vphantom{\frac{g({\bf s}_i)}{f({\bf s}_i)}-\hat I_n}\right)^{2}_{}$  . (3)

It is straightforward to show that this estimator has the following properties:
  1. E($ \hat{I}_{n}^{}$) = I
  2. $ \lim_{n\rightarrow\infty}^{}$$ \hat{I}_{n}^{}$ = I
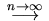  3. $ \sqrt{n}$ . ($ \hat{I}_{n}^{}$ - I)  $ \;\stackrel{n\rightarrow\infty}{\longrightarrow}\;$  Normal(0,$ \sigma_{f({\bf X})}^{2}$), where

    $\displaystyle \sigma_{f({\bf X})}^{2}$ = $\displaystyle \int_{\Omega}^{}$$\displaystyle \left(\vphantom{\frac{g({\bf X})}{f({\bf X})}-I}\right.$$\displaystyle {\frac{g({\bf X})}{f({\bf X})}}$ - I$\displaystyle \left.\vphantom{\frac{g({\bf X})}{f({\bf X})}-I}\right)^{2}_{}$f ($\displaystyle \bf X$) d$\displaystyle \bf X$ (4)

  4. E$ \left(\vphantom{\widehat{\sigma }^2(\hat I_n)}\right.$$ \widehat{\sigma }^{2}_{}$($ \hat{I}_{n}^{}$)$ \left.\vphantom{\widehat{\sigma }^2(\hat I_n)}\right)$ = $ \sigma^{2}_{}$($ \hat{I}_{n}^{}$) = $ \sigma_{f({\bf X})}^{2}$/n
The variance of $ \hat{I}_{n}^{}$ is proportional to $ \sigma_{f({\bf X})}^{2}$ and inversely proportional to the number of samples. To minimize the variance of $ \hat{I}_{n}^{}$, we can either increase the number of samples or try to decrease $ \sigma_{f({\bf X})}^{2}$. With respect to the latter, Rubinstein [1981] reports the following useful theorem and corollary.

Theorem 1   The minimum of $ \sigma_{f({\bf X})}^{2}$ is equal to

$\displaystyle \sigma_{f({\bf X})}^{2}$ = $\displaystyle \left(\vphantom{ \int_\Omega \left\vert g({\bf X})\right\vert d{\bf X} }\right.$$\displaystyle \int_{\Omega}^{}$$\displaystyle \left\vert\vphantom{ g({\bf X})}\right.$g($\displaystyle \bf X$)$\displaystyle \left.\vphantom{ g({\bf X})}\right\vert$d$\displaystyle \bf X$$\displaystyle \left.\vphantom{ \int_\Omega \left\vert g({\bf X})\right\vert d{\bf X} }\right)^{2}_{}$ - I2

and occurs when $ \bf X$ is distributed according to the following probability density function

f ($\displaystyle \bf X)$ = $\displaystyle {\frac{\left\vert g({\bf X)}\right\vert }{\int_\Omega \left\vert g({\bf X})\right\vert d{\bf X}}}$  .

Corollary 1   If g($ \bf X)>$0, then the optimal probability density function is

f ($\displaystyle \bf X)$ = $\displaystyle {\frac{g({\bf X)}}{I}}$

and $ \sigma_{f({\bf X})}^{2}$ = 0.

Although in practice sampling from precisely f ($ \bf X$) = g($ \bf X$)/I will occur rarely, we expect that functions that are close enough to it can still reduce the variance effectively. Usually, the closer the shape of the function f ($ \bf X$) is to the shape of the function g($ \bf X$), the smaller is $ \sigma_{f({\bf X})}^{2}$. In high-dimensional integrals, selection of the importance function, f ($ \bf X$), is far more critical than increasing the number of samples, since the former can dramatically affect $ \sigma_{f({\bf X})}^{2}$. It seems prudent to put more energy in choosing an importance function whose shape is as close as possible to that of g($ \bf X$) than to apply the brute force method of increasing the number of samples.

It is worth noting here that if f ($ \bf X$) is uniform, importance sampling becomes a general Monte Carlo sampling. Another noteworthy property of importance sampling that can be derived from Equation 4 is that we should avoid f ($ \bf X$) $ \ll$ $ \left\vert\vphantom{ g({\bf X})-I\cdot f({\bf X})}\right.$g($ \bf X$) - I . f ($ \bf X$)$ \left.\vphantom{ g({\bf X})-I\cdot f({\bf X})}\right\vert$ in any part of the domain of sampling, even if f ($ \bf X$) matches well g($ \bf X$)/I in important regions. If f ($ \bf X$) $ \ll$ $ \left\vert\vphantom{ g({\bf X})-I\cdot f({\bf X})}\right.$g($ \bf X$) - I . f ($ \bf X$)$ \left.\vphantom{ g({\bf X})-I\cdot f({\bf X})}\right\vert$, the variance can become very large or even infinite. We can avoid this by adjusting f ($ \bf X$) to be larger in unimportant regions of the domain of $ \bf X$.

While in this section we discussed importance sampling for continuous variables, the results stated are valid for discrete variables as well, in which case integration should be substituted by summation.

next up previous
Next: A Generic Importance Sampling Up: Importance Sampling Algorithms for Previous: Importance Sampling Algorithms for
Jian Cheng 2000-10-01